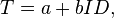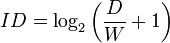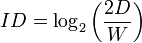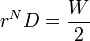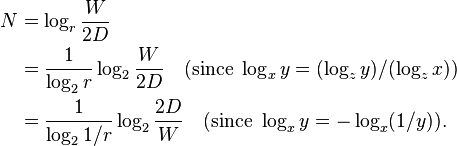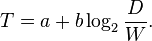Fitts's law

From Wikipedia, the free encyclopedia

Jump to: navigation, search
"fitt" redirects here. For the word used in Old English poetry, see Beowulf.

In human-computer interaction and ergonomics, Fitts's law (often cited as Fitts' law) is a model of human movement which predicts the time required to rapidly move to a target area, as a function of the distance to the target and the size of the target.

Fitts's law is used to model the act of pointing, both in the real world (e.g., with a hand or finger) and on computers (e.g., with a mouse). It was published by Paul Fitts in 1954.

Contents

[edit] Model

Mathematically, Fitts's law has been formulated in several different ways. One common form is the Shannon formulation (proposed by Scott MacKenzie, professor of York University, and named for its resemblance to the Shannon-Hartley theorem) for movement along a single dimension:

T = a + b \log_2 \Bigg(1+\frac{D}{W}\Bigg)

where:

  • T is the average time taken to complete the movement. (Traditionally, researchers have used the symbol MT for this, to mean movement time.)
  • a represents the start/stop time of the device and b stands for the inherent speed of the device. These constants can be determined experimentally by fitting a straight line to measured data.
  • D is the distance from the starting point to the center of the target. (Traditionally, researchers have used the symbol A for this, to mean the amplitude of the movement.)
  • W is the width of the target measured along the axis of motion. W can also be thought of as the allowed error tolerance in the final position, since the final point of the motion must fall within ±W⁄2 of the target's centre.

From the equation, we see a speed-accuracy tradeoff associated with pointing, whereby targets that are smaller and/or further away require more time to acquire.

[edit] Success and implications

Fitts's law is an unusually successful and well-studied model. Experiments that reproduce Fitts's results and/or that demonstrate the applicability of Fitts's law in somewhat different situations are not difficult to perform. The measured data in such experiments often fit a straight line with a correlation coefficient of 0.95 or higher, a sign that the model is very accurate.

Although Fitts only published two articles on his law (Fitts 1954, Fitts and Peterson 1964), there are hundreds of subsequent studies related to it in the human-computer interaction (HCI) literature, and quite possibly thousands of studies published in the larger psychomovement literature. The first HCI application of Fitts's law was by Card, English, and Burr (1978), who used the index of performance (IP), defined as 1⁄b, to compare performance of different input devices, with the mouse coming out on top. (This early work, according to Stuart Card's biography, "was a major factor leading to the mouse's commercial introduction by Xerox" [1].) Fitts's law has been shown to apply under a variety of conditions, with many different limbs (hands, feet, head-mounted sights, eye gaze), manipulanda (input devices), physical environments (including underwater), and user populations (young, old, special educational needs, and drugged participants). Note that the constants a, b, IP have different values under each of these conditions.

Since the advent of graphical user interfaces, Fitts's law has been applied to tasks where the user must position a mouse cursor over an on-screen target, such as a button or other widget. Fitts's law models both point-and-click and drag-and-drop actions. Dragging has a lower IP associated with it, because the increased muscle tension makes pointing more difficult.

In its original and strictest form:

  • It applies only to movement in a single dimension and not to movement in two dimensions (though it is successfully extended to two dimensions in the Accot-Zhai steering law);
  • It describes simple motor response of, say, the human hand, failing to account for software acceleration usually implemented for a mouse cursor;
  • It describes untrained movements, not movements that are executed after months or years of practice (though some argue that Fitts's law models behaviour that is so low level that extensive training doesn't make much difference).

If, as generally claimed, the law does hold true for pointing with the mouse, some consequences for user-interface design include:[citation needed]

  • Buttons and other GUI controls should be a reasonable size; it is relatively difficult to click on small ones.
  • Edges (e.g., the menu bar at top and Dock at bottom in Mac OS X) and corners of the computer display (e.g., "Start" button in the Luna theme of Windows XP and Apple & Spotlight menus of Mac OS X) are particularly easy to acquire because the pointer remains at the screen edge regardless of how much further the mouse is moved, thus can be considered as having infinite width.
  • Pop-up menus can usually be opened faster than pull-down menus, since the user avoids travel.
  • Pie menu items typically are selected faster and have a lower error rate than linear menu items, for two reasons: because pie menu items are all the same, small distance from the centre of the menu; and because their wedge-shaped target areas (which usually extend to the edge of the screen) are very large.

Fitts's law remains one of the few hard, reliable human-computer interaction predictive models, joined more recently by the Accot-Zhai steering law, which is derived from Fitts's law.

[edit] Mathematical details

The logarithm in Fitts's law is called the index of difficulty ID for the target, and has units of bits. We can rewrite the law as

T = a + b ID,\,

where

ID = \log_2 \left(\frac{D}{W}+1\right)

Thus, the units for b are time/bit; e.g., ms/bit. The constant a can be thought of as incorporating reaction time and/or the time required to click a button.

The values for a and b change as the conditions under which pointing is done are changed. For example, a mouse and stylus may both be used for pointing, but have different constants a and b associated with them.

An index of performance IP (also called throughput TP), in bits/time, can be defined to characterize how quickly pointing can be done, independent of the particular targets involved. There are two conventions for defining IP: one is IP = 1/b (which has the disadvantage of ignoring the effect of a), the other is IP = IDaverage/MTaverage (which has the disadvantage of depending on an arbitrarily chosen "average" ID). For a discussion of these two conventions, see Zhai (2002). Whatever definition is used, measuring the IP of different input devices allows the devices to be compared with respect to their pointing capability.

Slightly different from the Shannon formulation is the original formulation by Fitts:

ID = \log_2 \left(\frac{2D}{W}\right)

The factor of 2 here is not particularly important; this form of the ID can be rewritten with the factor of 2 absorbed as changes in the constants a, b. The "+1" in the Shannon form, however, does make it different from Fitts's original form, especially for low values of the ratio D/W. The Shannon form has the advantage that the ID is always non-negative, and has been shown to better fit measured data.

[edit] Derivation

Fitts's law can be derived from various models of motion. A very simple model, involving discrete, deterministic responses, is considered here. Although this model is overly simplistic, it provides some intuition for Fitts's law.

Assume that the user moves toward the target in a sequence of submovements. Each submovement requires a constant time t to execute, and moves a constant fraction 1-r of the remaining distance to the centre of the target, where 0 < r < 1. Thus, if the user is initially at a distance D from the target, the remaining distance after the first submovement is rD, and the remaining distance after the nth submovement is rnD. (In other words, the distance left to the target's centre is a function that decays exponentially over time.) Let N be the (possibly fractional) number of submovements required to fall within the target. Then,

r^N D = \frac{W}{2}

Solving for N:

\begin{align} N & = \log_r \frac{W}{2D} \\ & = \frac{1}{\log_2 r} \log_2 \frac{W}{2D}\quad(\text{since } \log_x y = (\log_z y)/(\log_z x)) \\ & = \frac{1}{\log_2 1/r} \log_2 \frac{2D}{W}\quad(\text{since } \log_x y = - \log_x(1/y)). \end{align}

The time required for all submovements is:

\begin{align} T = Nt & = \frac{t}{\log_2 1/r} \log_2 \frac{2D}{W} \\ & = \frac{t}{\log_2 1/r} + \frac{t}{\log_2 1/r} \log_2 \frac{D}{W}. \end{align}

By defining appropriate constants a and b, this can be rewritten as

T = a + b \log_2 \frac{D}{W}.

The above derivation is similar to one given in Card, Moran, and Newell (1983). For a critique of the deterministic iterative-corrections model, see Meyer et al. (1990).

[edit] See also

[edit] References

  1. ^ [1]
  • Paul M. Fitts (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology, volume 47, number 6, June 1954, pp. 381-391. (Reprinted in Journal of Experimental Psychology: General, 121(3):262–269, 1992).
  • Paul M. Fitts and James R. Peterson (1964). Information capacity of discrete motor responses. Journal of Experimental Psychology, 67(2):103–112, February 1964.
  • Stuart K. Card, William K. English, and Betty J. Burr (1978). Evaluation of mouse, rate-controlled isometric joystick, step keys, and text keys for text selection on a CRT. Ergonomics, 21(8):601–613, 1978.
  • I. Scott MacKenzie and William A. S. Buxton (1992). Extending Fitts' law to two-dimensional tasks. Proceedings of ACM CHI 1992 Conference on Human Factors in Computing Systems, pp. 219–226. http://doi.acm.org/10.1145/142750.142794
  • A. Murata. Extending effective target width in Fitts' law to a two-dimensional pointing task. International Journal of Human-Computer Interaction, 11(2):137–152, 1999. http://www.leaonline.com/doi/abs/10.1207/S153275901102_4
  • Johnny Accot and Shumin Zhai (2003). Refining Fitts' law models for bivariate pointing. Proceedings of ACM CHI 2003 Conference on Human Factors in Computing Systems, pp. 193–200. http://doi.acm.org/10.1145/642611.642646
  • Johnny Accot and Shumin Zhai (2002). More than dotting the i's — foundations for crossing-based interfaces. Proceedings of ACM CHI 2002 Conference on Human Factors in Computing Systems, pp. 73–80. http://doi.acm.org/10.1145/503376.503390
  • Stuart K. Card, Thomas P. Moran, Allen Newell (1983). The Psychology of Human-Computer Interaction.
  • I. Scott MacKenzie (1992). Fitts' law as a research and design tool in human-computer interaction. Human-Computer Interaction, volume 7, 1992, pp. 91–139. http://www.yorku.ca/mack/hci1992.pdf
  • Meyer, D. E., Smith, J. E. K., Kornblum, S., Abrams, R. A., & Wright, C. E. (1990). Speed-accuracy tradeoffs in aimed movements: Toward a theory of rapid voluntary action. In M. Jeannerod (Ed.), Attention and performance XIII (pp. 173–226). Hillsdale, NJ: Lawrence Erlbaum. http://www.umich.edu/~bcalab/Meyer_Bibliography.html
  • A. T. Welford (1968). Fundamentals of Skill. Methuen, 1968.
  • Shumin Zhai (2002). On the Validity of Throughput as a Characteristic of Computer Input, IBM Research Report RJ 10253, 2002, Almaden Research Center, San Jose, California. http://www.almaden.ibm.com/u/zhai/papers/ZhaiIBMReporRJ10253.pdf

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Fitts%27s_law"
Personal tools