Nelder-Mead method

From Wikipedia, the free encyclopedia

Jump to: navigation, search

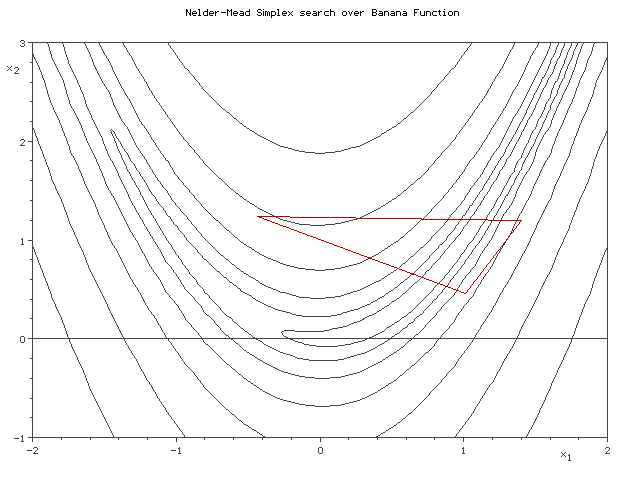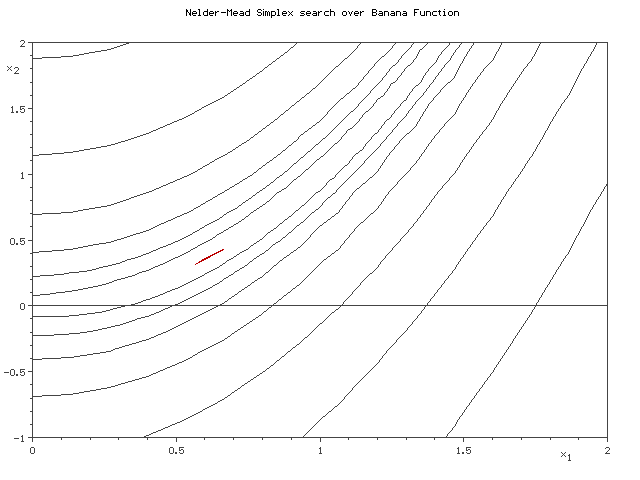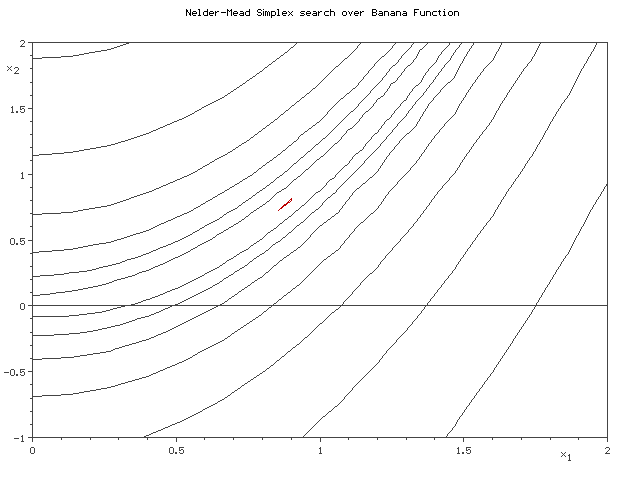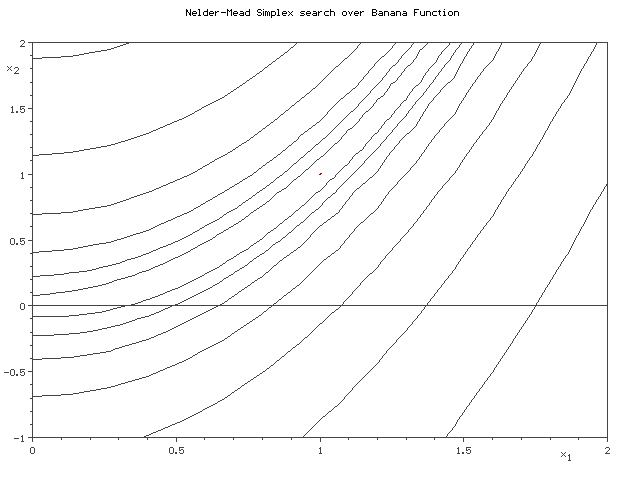
Nelder-Mead simplex search over the Rosenbrock banana function (above) and Himmelblau's function (below)
See simplex algorithm for the numerical solution of the linear programming problem.

The Nelder-Mead method or downhill simplex method or amoeba method is a commonly used nonlinear optimization algorithm. It is due to John Nelder & R. Mead (1965) and is a numerical method for minimizing an objective function in a many-dimensional space.

Contents

[edit] Overview

The method uses the concept of a simplex, which is a polytope of N + 1 vertices in N dimensions. Examples of simplexes include a line segment on a line, a triangle on a plane, a tetrahedron in three-dimensional space and so forth.

The method approximately finds a locally optimal solution to a problem with N variables when the objective function varies smoothly. For example, a suspension bridge engineer has to choose how thick each strut, cable, and pier must be. Clearly these all link together, but it is not easy to visualize the impact of changing any specific element. The engineer can use the Nelder-Mead method to generate trial designs which are then tested on a large computer model. As each run of the simulation is expensive, it is important to make good decisions about where to look. Nelder-Mead generates a new test position by extrapolating the behavior of the objective function measured at each test point arranged as a simplex. The algorithm then chooses to replace one of these test points with the new test point and so the algorithm progresses.

The simplest step is to replace the worst point with a point reflected through the centroid of the remaining N points. If this point is better than the best current point, then we can try stretching exponentially out along this line. On the other hand, if this new point isn't much better than the previous value, then we are stepping across a valley, so we shrink the simplex towards the best point.

Like all general purpose multidimensional optimization algorithms, Nelder-Mead occasionally gets stuck in a rut (because of the collapse of the simplex, see McKinnon below). The standard approach to handle this is to restart the algorithm with a new simplex starting at the current best value. This can be extended in a similar way to simulated annealing to escape small local minima.

Many variations exist depending on the actual nature of problem being solved. The most common, perhaps, is to use a constant size small simplex that climbs local gradients to local maxima. Visualize a small triangle on an elevation map flip flopping its way up a hill to a local peak. This, however, tends to perform poorly against the method described in this article because it makes small, unnecessary steps in areas of little interest.

This method is also known as the Flexible Polyhedron Method.

[edit] One possible variation of the NM algorithm

  • 1. Order according to the values at the vertices:
f(\textbf{x}_{1}) \leq f(\textbf{x}_{2}) \leq \cdots \leq f(\textbf{x}_{n+1})
  • 2. Calculate xo, the center of gravity of all points except xn + 1.
  • 3. Reflection
Compute reflected point \textbf{x}_{r} = \textbf{x}_{o} + \alpha (\textbf{x}_{o} - \textbf{x}_{n+1})
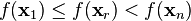If the reflected point is better than the worst, but not better than the best, i.e.: f(\textbf{x}_{1}) \leq f(\textbf{x}_{r}) < f(\textbf{x}_{n}),
then obtain a new simplex by replacing the worst point xn + 1 with the reflected point xr, and go to step 1.
  • 4. Expansion
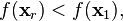
If the reflected point is the best point so far, f(\textbf{x}_{r}) < f(\textbf{x}_{1}),
then compute the expanded point \textbf{x}_{e} = \textbf{x}_{o} + \gamma (\textbf{x}_{o} - \textbf{x}_{n+1})
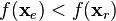
If the expanded point is better than the reflected point, f(\textbf{x}_{e}) < f(\textbf{x}_{r})
then obtain a new simplex by replacing the worst point xn + 1 with the expanded point xe, and go to step 1.
Else obtain a new simplex by replacing the worst point xn + 1 with the reflected point xr, and go to step 1.
Else (i.e. reflected point is worse than second worst) continue at step 5.
  • 5. Contraction:
Here, it is certain that f(\textbf{x}_{r}) \geq f(\textbf{x}_{n})
Compute contracted point \textbf{x}_{c} = \textbf{x}_{n+1}+\rho(\textbf{x}_{o}-\textbf{x}_{n+1})
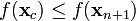
If the contracted point is better than the worst point, i.e. f(\textbf{x}_{c}) \leq f(\textbf{x}_{n+1})
then obtain a new simplex by replacing the worst point xn + 1 with the contracted point xc, and go to step 1.
Else go to step 6.
  • 6. Shrink step
For all but the best point, replace the point with
x_{i} = x_{1} + \sigma(x_{i} - x_{1}) \text{ for all i } \in\{2,\dots,n+1\}. go to step 1.

Note: \alpha, \, \gamma, \, \rho and σ are respectively the reflection, the expansion, the contraction and the shrink coefficient. Standard value are α = 1, γ = 2, ρ = 1 / 2 and σ = 1 / 2.

For the reflection, since xn + 1 is the vertex with the higher associated value along the vertices, we can expect to find a lower value at the reflection of xn + 1 in the opposite face formed by all vertices point xi except xn + 1.

For the expansion, if the reflection point xr is the new minimum along the vertices we can expect to find interesting values along the direction from xo to xr.

Concerning the contraction: If f(xr) > f(xn) we can expect that a better value will be inside the simplex formed by all the vertices xi.

The initial simplex is important, indeed, a too small initial simplex can lead to a local search, consequently the NM can get more easily stuck. So this simplex should depend on the nature of the problem.

[edit] See also

[edit] References

[edit] Further reading

  • J.A. Nelder and R. Mead, "A simplex method for function minimization", Computer Journal, 1965, vol 7, pp 308-313 [1]
  • Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
  • K.I.M. McKinnon, "Convergence of the Nelder-Mead simplex method to a non-stationary point", SIAM J Optimization, 1999, vol 9, pp148-158. [2] (algorithm summary online).

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Nelder-Mead_method"
Personal tools