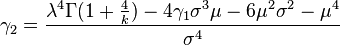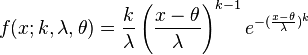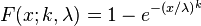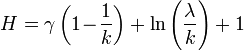Weibull distribution
From Wikipedia, the free encyclopedia
Probability density function |
|
Cumulative distribution function |
|
| Parameters |  scale (real) scale (real) shape (real) shape (real) |
|---|---|
| Support |  |
| Probability density function (pdf) |  |
| Cumulative distribution function (cdf) |  |
| Mean | 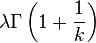 |
| Median | 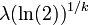 |
| Mode |  if k > 1 if k > 1 |
| Variance | 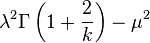 |
| Skewness | 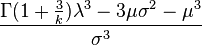 |
| Excess kurtosis | (see text) |
| Entropy | 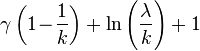 |
| Moment-generating function (mgf) | see Weibull fading |
| Characteristic function | see [[Muraleedharan.et.al.,(2007)Coastal Engineering 54 (8), 630-638.
http://dx.doi.org/10.1016/j.coastaleng.2007.05.001 see Reply to Saralees Nadarajah,(2008)Coastal Engineering 55 (2), 191-193 http://dx.doi.org/10.1016/j.coastaleng.2007.07.006]] |
In probability theory and statistics, the Weibull distribution[1] (named after Waloddi Weibull) is a continuous probability distribution. It is often called the Rosin–Rammler distribution when used to describe the size distribution of particles. The distribution was introduced by P. Rosin and E. Rammler in 1933.[2][3] The probability density function of a Weibull random variable x is[4]:
where k > 0 is the shape parameter and λ > 0 is the scale parameter of the distribution. Its complementary cumulative distribution function is a stretched exponential function.
The Weibull distribution is often used in the field of life data analysis due to its flexibility—it can mimic the behavior of other statistical distributions such as the normal and the exponential. If the failure rate decreases over time, then k < 1. If the failure rate is constant over time, then k = 1. If the failure rate increases over time, then k > 1.
An understanding of the failure rate may provide insight as to what is causing the failures:
- A decreasing failure rate would suggest "infant mortality". That is, defective items fail early and the failure rate decreases over time as they fall out of the population.
- A constant failure rate suggests that items are failing from random events.
- An increasing failure rate suggests "wear out" - parts are more likely to fail as time goes on.
Under certain parameterizations, the Weibull distribution reduces to several other familiar distributions:
- When k = 1, it is the exponential distribution.
- When k = 2, it becomes equivalent to the Rayleigh distribution, which models the modulus of a two-dimensional uncorrelated bivariate normal vector. In this case, the Rayleigh variance σ2 is equal to λ2 / 2.
- When k = 3.4, it appears similar to the normal distribution.
- As k goes to infinity, the Weibull distribution asymptotically approaches the Dirac delta function.
Contents |
[edit] Properties
Characteristic Function of Weibull Distribution
The Characteristic Function (φ(t)) of Weibull distribution is given by Muraleedharan; et al (2007), Coastal Engineering, 54, pp. 630-638. It can generate all the moments of Weibull distribution and hence characteristic functions are also known as moment generating functions(mgf). It also gives all the moments of Rayleigh and exponential distributions for b (shape parameter)equal to 2 and 1 respectively. Also it gives the characteristic and moment generating functions of Rayleigh and exponential distributions for b equal to 2 and 1 respectively. It satisfied all the conditions for a function to be a characteristic function (See Reply to Saralees Nadarajah (2008),Coastal Engineering 55(2),191-193).
Also by Taylor's Theorem for complex functions,the characteristic function of any random variable, X, with finite mean μ can be written as
φ(t)=1+itμ+0(t); t→0
This is also true for the characteristic function of Weibull,Rayleigh (b=2) and exponential (b=1) distributions as
μ= aГ(1+1/b)
Hence the characteristic function given by Muraleedharan et.al(2007) is correct. ______________________________________________________________________________________________
There is an abrupt change in the value of the density function at 0 when k takes on values around 1. It is because,[5]
- for any
 as
as 
- for
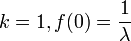 , and
, and - for any
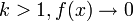 as
as 
The nth raw moment is given by:
where Γ is the Gamma function. The mean and variance of a Weibull random variable can be expressed as:
and
The skewness is given by:
The excess kurtosis is given by:
where Γi = Γ(1 + i / k). The kurtosis excess may also be written as :
A generalized, 3-parameter Weibull distribution is also often found in the literature. It has the probability density function
for 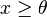 and f(x; k, λ, θ) = 0 for x < θ, where k > 0 is the shape parameter, λ > 0 is the scale parameter and θ is the location parameter of the distribution. When θ=0, this reduces to the 2-parameter distribution.
and f(x; k, λ, θ) = 0 for x < θ, where k > 0 is the shape parameter, λ > 0 is the scale parameter and θ is the location parameter of the distribution. When θ=0, this reduces to the 2-parameter distribution.
The cumulative distribution function for the 2-parameter Weibull is
for x ≥ 0, and F(x; k; λ) = 0 for x < 0.
The cumulative distribution function for the 3-parameter Weibull is
for x ≥ θ, and F(x; k, λ, θ) = 0 for x < θ.
The failure rate h (or hazard rate) is given by
[edit] Information entropy
The information entropy is given by
where γ is the Euler–Mascheroni constant.
[edit] Generating Weibull-distributed random variates
Given a random variate U drawn from the uniform distribution in the interval (0, 1), then the variate
has a Weibull distribution with parameters k and λ. This follows from the form of the cumulative distribution function. Note that if you are generating random numbers belonging to (0,1), exclude zero values to avoid the natural log of zero.
[edit] Related distributions
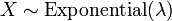 is an exponential distribution if X˜Weibull(k = 1,λ − 1).
is an exponential distribution if X˜Weibull(k = 1,λ − 1).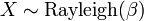 is a Rayleigh distribution if
is a Rayleigh distribution if  .
. is a Weibull distribution if
is a Weibull distribution if 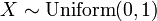 .
.- Inverse Weibull distribution with p.d.f.

- See also the generalized extreme value distribution.
[edit] Uses
The Weibull distribution is used
- In survival analysis
- To represent manufacturing and delivery times in industrial engineering
- In extreme value theory
- In weather forecasting
- In reliability engineering and failure analysis
- In radar systems to model the dispersion of the received signals level produced by some types of clutters
- To model fading channels in wireless communications, as the Weibull fading model seems to exhibit good fit to experimental fading channel measurements
- In General insurance to model the size of Reinsurance claims, and the cumulative development of Asbestosis losses
- In forecasting technological change (also known as the Sharif-Islam model)
- To describe wind speed distributions, as the natural distribution often matches the Weibull shape
The Weibull distribution may be used in place of the normal distribution because a Weibull variate can be generated through inversion. Normal variates are typically generated using the more complicated Box-Muller method, which requires two uniform random variates.
The 2-Parameter Weibull distribution is used to describe the particle size distribution of particles generated by grinding, milling and crushing operations. The Rosin-Rammler distribution predicts fewer fine particles than the Log-normal distribution. It is generally most accurate for narrow PSDs.
Using the cumulative distribution function:
- F(x; k; λ) is the mass fraction of particles with diameter < x
- λ is the mean particle size
- k is a measure of particle size spread
[edit] References
- ^ Weibull, W. (1951) "A statistical distribution function of wide applicability" J. Appl. Mech.-Trans. ASME 18(3), 293-297
- ^ http://www.zarm.uni-bremen.de/gamm98/num_abs/a912.html
- ^ Rosin, P., and Rammler, E. (1933) "The Laws Governing the Fineness of Powdered Coal", Journal of the Institute of Fuel, vol. 7, pp. 29 - 36.
- ^ Papoulis, Pillai, "Probability, Random Variables, and Stochastic Processes, 4th Edition
- ^ http://www.weibull.com/LifeDataWeb/characteristics_of_the_weibull_distribution.htm
[edit] Bibliography
- Nelson, Jr, Ralph (2008-02-05). "Dispersing Powders in Liquids, Part 1, Chap 6: Particle Volume Distribution". http://www.erpt.org/014Q/nelsa-06.htm. Retrieved on 2008-02-05.
[edit] External links
- A Statistical Distribution Function of Wide Applicability (the original 1951 article).
- The Weibull distribution (with examples, properties, and calculators).
- The Weibull plot.
- Weibull plotting paper.
- Mathpages - Weibull Analysis
- Using Excel for Weibull Analysis
This article from the Quality Digest describes how to use MS Excel to analyse lifetest data with the Weibull statistical distribution. Although Excel doesn't have an inverse Weibull function, this article shows how to use Excel to solve for critical values. - Biography of Waloddi Weibull.
- The SOCR Resource provides interactive interface to Weibull distribution.


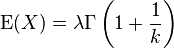
![\textrm{var}(X) = \lambda^2\left[\Gamma\left(1+\frac{2}{k}\right) - \Gamma^2\left(1+\frac{1}{k}\right)\right]\,.](http://upload.wikimedia.org/math/f/7/c/f7c95c93bf51d2722a76916f81377acb.png)
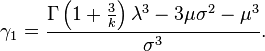
![\gamma_2=\frac{-6\Gamma_1^4+12\Gamma_1^2\Gamma_2-3\Gamma_2^2
-4\Gamma_1\Gamma_3+\Gamma_4}{[\Gamma_2-\Gamma_1^2]^2}](http://upload.wikimedia.org/math/6/4/2/642e218125f24368120e15265357cdc1.png)