Present value
From Wikipedia, the free encyclopedia
Present value is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk. Present value calculations are widely used in business and economics to provide a means to compare cash flows at different times on a meaningful "like to like" basis.
Contents |
[edit] Background
Money value fluctuates over time: $100 today are not worth $100 in five years. This is because you can invest your $100 today in a bank account or any other (safe) investment that will return you an interest. Also, if $100 today allows you to purchase an item today, it is possible that the same $100 amount is not enough to purchase the same item in five years, because of inflation (increase in purchase price).
An investor who has some money has two options: to spend it right now or to save it. But the financial compensation for saving it (and not spending it) is that the money value will accrue through the interests that he will receive from a borrower (the bank account on which he has the money deposited).
Therefore, to evaluate the real worthiness of an amount of money today after a given period of time, economic agents compound the amount of money at a given (interest) rate. Most actuarial calculations use the risk-free interest rate which corresponds the minimum guaranteed rate provided by your bank's saving account for example. If you want to compare your change in purchasing power, then, you should use the real interest rate (nominal interest rate minus inflation rate).
The operation of evaluating a present value into the future value is called a capitalization (how much $100 today are worth in 5 years?). The reverse operation which consists in evaluating the present value of a future amount of money is called a discounting (how much $100 that I will receive in 5 years -at a lottery for example- are worth today?).
It follows that if one has to choose between receiving $100 today and $100 in one year, the rational decision is to cash the $100 today. If the money is to be received in one year and assuming the savings account interest rate is 5%, the person has to be offered at least $105 in one year so that two options are equivalent (either receiving $100 today or receiving $105 in one year). This is because if you cash $100 today and deposit in your savings account, you will have $105 in one year.
[edit] Calculation
The most commonly applied model of the time value of money is compound interest. To someone who can lend or borrow for  years at an interest rate
years at an interest rate  per year (where interest of "5 percent" is expressed fully as 0.05), the present value of the receiving
per year (where interest of "5 percent" is expressed fully as 0.05), the present value of the receiving  monetary units
monetary units  years in the future is:
years in the future is:
This is also found from the formula for the future value with negative time.
The purchasing power in today's money of an amount C of money, t years into the future, can be computed with the same formula, where in this case i is an assumed future inflation rate.
The expression  enters almost all calculations of present value. Where the interest rate is expected to be different over the term of the investment, different values for
enters almost all calculations of present value. Where the interest rate is expected to be different over the term of the investment, different values for  may be included; an investment over a two year period would then have PV of:
may be included; an investment over a two year period would then have PV of:
[edit] Technical details
Present value is additive. The present value of a bundle of cash flows is the sum of each one's present value.
In fact, the present value of a cashflow at a constant interest rate is mathematically the same as the Laplace transform of that cashflow evaluated with the transform variable (usually denoted "s") equal to the interest rate. For discrete time, where payments are separated by large time periods, the transform reduces to a sum, but when payments are ongoing on an almost continual basis, the mathematics of continuous functions can be used as an approximation.
[edit] Choice of interest rate
The interest rate used is the risk-free interest rate. If there are no risks involved in the project, the expected rate of return from the project must equal or exceed this rate of return or it would be better to invest the capital in these risk free assets. If there are risks involved in an investment this can be reflected through the use of a risk premium. The risk premium required can be found by comparing the project with the rate of return required from other projects with similar risks. Thus it is possible for investors to take account of any uncertainty involved in various investments.
[edit] Annuities, perpetuities and other common forms
Many financial arrangements (including bonds, other loans, leases, salaries, membership dues, annuities, straight-line depreciation charges) stipulate structured payment schedules, which is to say payment of the same amount at regular time intervals. The term "annuity" is often used to refer to any such arrangement when discussing calculation of present value. The expressions for the present value of such payments are summations of geometric series.
A cash flow stream with a limited number (n) of periodic payments (C), receivable at times 1 through n, is an annuity. Future payments are discounted by the periodic rate of interest (i). The present value of this ordinary annuity is determined with this formula:[1]
A periodic amount receivable indefinitely is called a perpetuity, although few such instruments exist. The present value of a perpetuity can be calculated by taking the limit of the above formula as n approaches infinity. The bracketed term reduces to one leaving:
The first formula is found from subtracting from the latter result the present value of a perpetuity delayed n periods.
These calculations must be applied carefully, as there are underlying assumptions:
- That it is not necessary to account for price inflation, or alternatively, that the cost of inflation is incorporated into the interest rate.
- That the likelihood of receiving the payments is high — or, alternatively, that the default risk is incorporated into the interest rate.
See time value of money for further discussion.
[edit] References
- ^ "Annuities: Present and Future Value". http://www.college-cram.com/study/finance/presentations/1116. Retrieved on 2008-07-10.

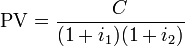
![PV \,=\,\frac{C}{i}\cdot[1-\frac{1}{\left(1+i\right)^n}]](http://upload.wikimedia.org/math/3/f/5/3f5ee1d6ee77bc54f36862f83adea03d.png)


