%5Bwikipedia_article%5D [compilation] archive art chaostheory clasefractales cool dimension dimensiones educación ee fractal fractal-dimension fractales fractals geometry geometría graphics hausdorff ilwaco images list maf math mathematics maths pictures
List of fractals by Hausdorff dimension
From Wikipedia, the free encyclopedia
According to Falconer, one of the essential features of a fractal is that its Hausdorff dimension strictly exceeds its topological dimension.[1] Presented here is a list of fractals ordered by increasing Hausdorff dimension, with the purpose of visualizing what it means for a fractal to have a low or a high dimension.
Contents |
[edit] Deterministic fractals
| Hausdorff dimension (exact value) |
Hausdorff dimension (approx.) |
Name | Illustration | Remarks |
|---|---|---|---|---|
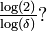 |
0.4498? | Logistic map bifurcations |  |
In the bifurcation diagram, when approaching the chaotic zone, a succession of period doubling appears, in a geometric progression tending to 1/δ. (δ = Feigenbaum constant = 4.6692.) |
 |
0.6309 | Cantor set | Built by removing the central third at each iteration. Nowhere dense and not a countable set. | |
 |
0.88137 | Spectrum of Fibonacci Hamiltonian | The study the spectrum of the Fibonacci Hamiltonian proves upper and lower bounds for its fractal dimension in the large coupling regime. These bounds show that the spectrum converges to an explicit constant.[2] | |
 |
1 | Smith-Volterra-Cantor set | Built by removing a central interval of length 1 / 22n of each remaining interval at the nth iteration. Nowhere dense but has a Lebesgue measure of ½. | |
 |
1.0686 | contour of the Gosper island |  |
|
| Measured (box counting) | 1.2 | Dendrite Julia set |  |
Julia set for parameters: Real = 0 and Imaginary = 1. |
 |
1.2083 | Fibonacci fractal 60° |  |
Build from the Fibonacci word. See also the standard Fibonacci fractal.
|
| 1.26 | Hénon map |  |
The canonical Hénon map (with parameters a = 1.4 and b = 0.3) has Hausdorff dimension 1.261 ± 0.003. Different parameters yield different dimension values. | |
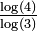 |
1.2619 | Koch curve |  |
3 von Koch curves form the Koch snowflake or the anti-snowflake. |
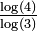 |
1.2619 | boundary of Terdragon curve |  |
L-system: same as dragon curve with angle = 30°. The Fudgeflake is based on 3 initial segments placed in a triangle. |
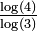 |
1.2619 | 2D Cantor dust |  |
Cantor set in 2 dimensions. |
| calculated | 1.2683 | Julia set z2 − 1 |  |
Julia set for c = −1. [3] |
| 1.3057 | Apollonian gasket |  |
see [4] | |
| calculated | 1.3934 | Douady rabbit | 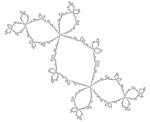 |
Julia set for c = −0,123 + 0.745i. [5] |
 |
1.4649 | Vicsek fractal |  |
Built by exchanging iteratively each square by a cross of 5 squares. |
 |
1.4649 | Quadratic von Koch curve (type 1) | 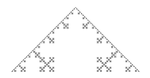 |
One can recognize the pattern of the Vicsek fractal (above). |
 |
1.5000 | Quadratic von Koch curve (type 2) |  |
Also called "Minkowski sausage". |
![\textstyle{\frac{\log\left(\frac{1+\sqrt[3]{73-6\sqrt{87}}+\sqrt[3]{73+6\sqrt{87}}}{3}\right)}
{\log(2)}}](http://upload.wikimedia.org/math/b/2/0/b20412764066b5d7378580b90852dfd7.png) |
1.5236 | Dragon curve boundary |  |
cf. Chang & Zhang.[6][7] |
 |
1.585 | 3-branches tree |  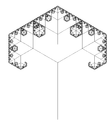 |
Each branch carries 3 branches (here 90° and 60°). The fractal dimension of the entire tree is the fractal dimension of the terminal branches. NB: the 2-branches tree has a fractal dimension of only 1. |
 |
1.585 | Sierpinski triangle |  |
Also the triangle of Pascal modulo 2. |
 |
1.585 | Sierpiński arrowhead curve |  |
Same limit as the triangle (above) but built with a one-dimensional curve. |
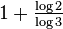 |
1.6309 | Pascal triangle modulo 3 |  |
For a triangle modulo k, if k is prime, the fractal dimension is  (cf. Stephen Wolfram[8]). (cf. Stephen Wolfram[8]). |
 |
1.6379 | Fibonacci fractal | 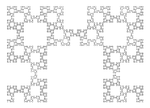 |
Fractal based on the Fibonacci word (or Rabbit sequence) Sloane A005614. Illustration : Fractal curve after 23 steps (F23 = 28657 segments). [9]
|
 |
1.6826 | Pascal triangle modulo 5 |  |
For a triangle modulo k, if k is prime, the fractal dimension is  (cf. Stephen Wolfram[8]). (cf. Stephen Wolfram[8]). |
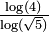 |
1.7227 | Pinwheel fractal | 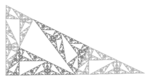 |
Built with Conway's Pinwheel tile. |
 |
1.7712 | Hexaflake |  |
Built by exchanging iteratively each hexagon by a flake of 7 hexagons. Its boundary is the von Koch flake and contains an infinity of Koch snowflakes (black or white). |
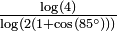 |
1.7848 | Von Koch curve 85°, Cesaro fractal |  |
Generalizing the von Koch curve with an angle a chosen between 0 and 90°. The fractal dimension is then ![\scriptstyle{\frac{\log(4)}{\log(2(1+\cos(a)))}} \in [1,2]](http://upload.wikimedia.org/math/b/4/c/b4c3c4d6edeb610a112e169ce6857c5d.png) . The Cesaro fractal is based on this pattern. . The Cesaro fractal is based on this pattern. |
 |
1.8617 | Pentaflake |  |
Built by exchanging iteratively each pentagon by a flake of 6 pentagons.
|
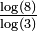 |
1.8928 | Sierpinski carpet |  |
Each face of the Menger sponge is a Sierpinski carpet, as is the bottom surface of the 3D quadratic Koch surface (type 1). |
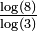 |
1.8928 | 3D Cantor dust |  |
Cantor set in 3 dimensions. |
| Estimated | 1.9340 | Boundary of the Lévy C curve |  |
Estimated by Duvall and Keesling (1999). The curve itself has a fractal dimension of 2. |
| 1.974 | Penrose tiling |  |
See Ramachandrarao, Sinha & Sanyal[10]. | |
 |
2 | Boundary of the Mandelbrot set |  |
The boundary and the set itself have the same dimension [11]. |
 |
2 | Julia set |  |
For determined values of c (including c belonging to the boundary of the Mandelbrot set), the Julia set has a dimension of 2. [12]. |
 |
2 | Sierpiński curve |  |
Every Peano curve filling the plane has a Hausdorff dimension of 2. |
 |
2 | Hilbert curve |  |
|
 |
2 | Peano curve |  |
And a family of curves built in a similar way, such as the Wunderlich curves. |
 |
2 | Moore curve |  |
Can be extended in 3 dimensions. |
| 2 | Lebesgue curve or z-order curve |  |
Unlike the previous ones this space-filling curve is differentiable almost everywhere. Another type can be defined in 2D. Like the Hilbert Curve it can be extended in 3D.[13] | |
 |
2 | Dragon curve |  |
And its boundary has a fractal dimension of 1.5236270862[14]. |
| 2 | Terdragon curve |  |
L-system: F → F + F – F, angle = 120°. | |
 |
2 | T-Square | ||
 |
2 | Gosper curve |  |
Its boundary is the Gosper island. |
 |
2 | Sierpiński tetrahedron |  |
Each tetrahedron is replaced by 4 tetrahedra. |
 |
2 | H-fractal |  |
Also the « Mandelbrot tree » which has a similar pattern. |
 |
2 | Pythagoras tree |  |
Every square generates 2 squares with a reduction ratio of sqrt(2)/2. |
 |
2 | 2D Greek cross fractal |  |
Each segment is replaced by a cross formed by 4 segments. |
| 2.06 | Lorenz attractor |  |
For precise values of parameters. McGuinness (1983)[15] | |
 |
2.3296 | Dodecahedron fractal |  |
Each dodecahedron is replaced by 20 dodecahedra.
|
 |
2.3347 | 3D quadratic Koch surface (type 1) |  |
Extension in 3D of the quadratic Koch curve (type 1). The illustration shows the second iteration. |
| 2.4739 | Apollonian sphere packing |  |
The interstice left by the apollolian spheres. Apollonian gasket in 3D. Dimension calculated by M. Borkovec, W. De Paris, and R. Peikert.[16] | |
 |
2.50 | 3D quadratic Koch surface (type 2) |  |
Extension in 3D of the quadratic Koch curve (type 2). The illustration shows the second iteration. |
 |
2.5237 | Cantor tesseract | no image available | Cantor set in 4 dimensions. Generalization: in a space of dimension n, the Cantor set has a Hausdorff dimension of 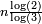 . . |
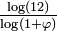 |
2.5819 | Icosahedron fractal |  |
Each icosahedron is replaced by 12 icosahedra. 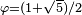 (golden ratio). (golden ratio). |
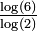 |
2.5849 | 3D Greek cross fractal |  |
Each segment is replaced by a cross formed by 6 segments. |
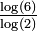 |
2.5849 | Octahedron fractal |  |
Each octahedron is replaced by 6 octahedra. |
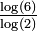 |
2.5849 | von Koch surface | 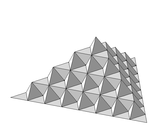 |
Each equilateral triangle is replaced by 6 triangles, twice smaller. |
 |
2.7268 | Menger sponge |  |
And its surface has a fractal dimension of 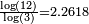 . . |
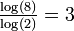 |
3 | 3D Hilbert curve |  |
A Hilbert curve extended to 3 dimensions. |
 |
3 | 3D Lebesgue curve |  |
A Lebesgue curve extended to 3 dimensions. |
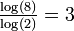 |
3 | 3D Moore curve |  |
A Moore curve extended to 3 dimensions. |
[edit] Random and natural fractals
| Hausdorf dimension (exact value) |
Hausdorf dimension (approx.) |
Name | Illustration | Remarks |
|---|---|---|---|---|
| Measured | 1.25 | Coastline of Great Britain |  |
Fractal dimension of the west coast of Great Britain, as measured by Lewis Fry Richardson and cited by Benoît Mandelbrot.[17] |
 |
1.33 | Boundary of Brownian motion | 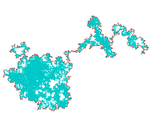 |
(cf. Lawler, Schramm, Werner).[18] |
 |
1.33 | 2D polymer | Similar to the brownian motion in 2D with non self-intersection. [19]. | |
 |
1.33 | Percolation front in 2D, Corrosion front in 2D |  |
Fractal dimension of the percolation-by-invasion front, at the percolation threshold (59.3%). It’s also the fractal dimension of a stopped corrosion front [19]. |
| 1.40 | Clusters of clusters 2D | When limited by diffusion, clusters combine progressively to a unique cluster of dimension 1.4. [19] | ||
| Measured | 1.52 | Coastline of Norway |  |
See J. Feder. [20] |
| Measured | 1.55 | Random walk with no self-intersection |  |
Self-avoiding random walk in a square lattice, with a « go-back » routine for avoiding dead ends. |
 |
1.66 | 3D polymer | Similar to the brownian motion in a cubic lattice, but without self-intersection [19]. | |
| 1.70 | 2D DLA Cluster |  |
In 2 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 1.70 [19]. | |
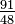 |
1.8958 | 2D percolation cluster |  |
Under the percolation threshold (59.3%) the percolation-by-invasion cluster has a fractal dimension of 91/48 [19]. Beyond that threshold, le cluster is infinite and 91/48 becomes the fractal dimension of the « clearings ». |
 |
2 | Brownian motion |  |
Or random walk. The Hausdorff dimensions equals 2 in 2D, in 3D and in all greater dimensions (K.Falconer "The geometry of fractal sets"). |
 |
2.33 | Cauliflower |  |
Every branch carries around 13 branches 3 times smaller. |
| 2.5 | Balls of crumpled paper |  |
When crumpling sheets of different sizes but made of the same type of paper and with the same aspect ratio (for example, different sizes in the ISO 216 A series), then the diameter of the balls so obtained elevated to a non-integer exponent between 2 and 3 will be approximately proportional to the area of the sheets from which the balls have been made. [1] Creases will form at all size scales (see Universality (dynamical systems)). | |
| 2.50 | 3D DLA Cluster |  |
In 3 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 2.50 [19]. | |
| 2.50 | Lichtenberg figure |  |
Their appearance and growth appear to be related to the process of diffusion-limited aggregation or DLA [19]. | |
| Measured | 2.66 | Broccoli |  |
[21] |
| 2.79 | Surface of human brain |  |
[22] | |
| 2.97 | Lung surface | 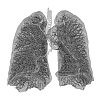 |
The alveoli of a lung form a fractal surface close to 3 [19]. | |
| Calculated | 3 | Quantum string drifting randomly |  |
Hausdorff dimension of a quantum string whose representative point randomly drifts through loop space.[23] |
| Calculated |  |
Multiplicative cascade |  |
This is an example of a multifractal distribution. However by choosing its parameters in a particular way we can force the distribution to become a monofractal[24]. |
[edit] See also
| Wikimedia Commons has media related to: fractals |
[edit] Notes
- ^ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd.. xxv. ISBN 0-470-84862-6.
- ^ Fractal dimension of the spectrum of the Fibonacci Hamiltonian
- ^ fractal dimension of the z²-1 Julia set
- ^ fractal dimension of the apollonian gasket
- ^ fractal dimension of the Douady rabbit
- ^ Fractal dimension of the boundary of the dragon fractal
- ^ Recurrent construction of the boundary of the dragon curve
- ^ a b Fractal dimension of the Pascal triangle modulo k
- ^ A005614 Fibonacci word or rabbit sequence at Sloane's OEIS
- ^ Fractal dimension of a Penrose tiling
- ^ Fractal dimension of the boundary of the Mandelbrot set
- ^ Fractal dimension of certain Julia sets
- ^ Lebesgue curve variants
- ^ Complex base numeral systems
- ^ The fractal dimension of the Lorenz attractor, Mc Guinness (1983)
- ^ Fractal dimension of the apollonian sphere packing
- ^ How long is the coast of Britain? Statistical self-similarity and fractional dimension, B. Mandelbrot
- ^ Fractal dimension of the brownian motion boundary
- ^ a b c d e f g h i Bernard Sapoval "Universalités et fractales", Flammarion-Champs (2001), ISBN=2-080-81466-4
- ^ Feder, J., "Fractals,", Plenum Press, New York, (1988).
- ^ Fractal dimension of the broccoli
- ^ Fractal dimension of the surface of the human brain
- ^ The Hausdorf dimension of a quantum string
- ^ [Meakin (1987)]
[edit] References
- 1Kenneth Falconer, Fractal Geometry, John Wiley & Son Ltd; ISBN 0-471-92287-0 (March 1990)
[edit] Further reading and references
- Benoît Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman & Co; ISBN 0-7167-1186-9 (September 1982).
- Heinz-Otto Peitgen, The Science of Fractal Images, Dietmar Saupe (editor), Springer Verlag, ISBN 0-387-96608-0 (August 1988)
- Michael F. Barnsley, Fractals Everywhere, Morgan Kaufmann; ISBN 0-12-079061-0
- Bernard Sapoval, « Universalités et fractales », collection Champs, Flammarion. ISBN 2080814664 (2001).

