Circle of fifths
From Wikipedia, the free encyclopedia
| This article needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (July 2008) |

In music theory, the circle of fifths (or circle of fourths) shows the relationships among the twelve tones of the chromatic scale, their corresponding key signatures, and the associated major and minor keys. More generally, it is a geometrical representation of relationships among the 12 pitch classes of the chromatic scale in pitch class space. Musicians and composers use the circle of fifths to understand and describe those relationships.
At the top of the circle, the key of C has no sharps or flats. Starting from there and going clockwise by ascending fifths, the key of G has one sharp, the key of D has 2 sharps, and so on. Similarly, going counterclockwise from the top by descending fifths, the key of F has one flat, the key of B♭ has 2 flats, and so on. At the bottom of the circle, the sharp and flat keys overlap, showing pairs of enharmonic key signatures.
Starting at any pitch, ascending by the interval of an equal tempered perfect fifth, one passes all twelve tones, to return to the beginning pitch. (Ascending by justly tuned perfect fifths fails to close the circle by a small amount, the Pythagorean comma.) Reversing the direction, playing tones separated by a perfect fourth, gives the same result. (To the ear, the sequence of fourths gives an impression of settling, or resolution. (see cadence))
Contents |
[edit] Structure and use
Pitches within the chromatic scale are related not only by the number of semitones between them within the chromatic scale, but also related harmonically within the circle of fifths. Reading the circle of fifths as descending pitches going clockwise, or ascending counterclockwise, gives the circle of fourths. Typically "circle of fifths" is used in the analysis of classical music, whereas "circle of fourths" is used in the analysis of Jazz music, but this distinction is not exclusive.
[edit] Diatonic key signatures
The circle is commonly used to represent the relationship between diatonic scales. Here, the letters on the circle are taken to represent the major scale with that note as tonic. The numbers on the inside of the circle show how many sharps or flats the key signature for this scale has. Thus a major scale built on A has 3 sharps in its key signature. The major scale built on F has 1 flat.
For minor scales, rotate the letters counter-clockwise by 3, so that e.g. A minor has 0 sharps or flats and E minor has 1 sharp. (See relative key for details.)
[edit] Modulation and chord progression
Tonal music often modulates by moving between adjacent scales on the circle of fifths. This is because diatonic scales contain seven pitch classes that are contiguous on the circle of fifths. It follows that diatonic scales a perfect fifth apart share six of their seven notes. Furthermore, the notes not held in common differ by only a semitone. Thus modulation by perfect fifth can be accomplished in an exceptionally smooth fashion. For example, to move from the C major scale F - C - G - D - A - E - B to the G major scale C - G - D - A - E - B - F♯, one need only move the C major scale's "F" to "F♯."
In Western tonal music, one also finds chord progressions between chords whose roots are related by perfect fifth. For instance, root progressions such as D-G-C are common. For this reason, the circle of fifths can often be used to represent "harmonic distance" between chords.
According to theorists including Goldman, harmonic function (the use, role, and relation of chords in harmony), including, "functional succession," may be, "explained by the circle of fifths (in which, therefore, scale degree II is closer to the dominant than scale degree IV),"[1]. In this view the tonic is considered the end of the line towards which a chord progression derived from the circle of fifths progresses.
According to Goldman's Harmony in Western Music, "the IV chord is actually, in the simplest mechanisms of diatonic relationships, at the greatest distance from I. In terms of the [descending] circle of fifths, it leads away from I, rather than toward it." [2] Thus the progression I-ii-V-I (an authentic cadence) would feel more final or resolved than I-IV-I (a plagal cadence. Goldman [3], as well as Nattiez, also argue that, "the chord on the fourth degree appears long before the chord on II, and the subsequent final I, in the progression I-IV-viio-iii-vi-ii-V-I," and is farther from the tonic there as well. [4]
Goldman argues that, "historically the use of the IV chord in harmonic design, and especially in cadences, exhibits some curious features. By and large, one can say that the use of IV in final cadences becomes more common in the nineteenth century than it was in the eighteenth, but that it may also be understood as a substitute for the ii chord when it proceeds V. It may also be quite logically construed as an incomplete ii7 chord (lacking root)." [5] The delayed acceptance of the IV-I in final cadences is explained aesthetically by its lack of closure, caused by its position in the circle of fifths. The earlier use of IV-V-I is explained by proposing a relation between IV and ii, allowing IV to substitute for or serve as ii. However, Nattiez calls this latter argument, "a narrow escape: only the theory of a ii chord without a root allows Goldman to maintain that the circle of fifths is completely valid from Bach to Wagner," or the entire common practice period. [6]
[edit] In lay terms
|
Playing the circle of fifths
|
A simple way to see the musical interval known as a fifth is by looking at a piano keyboard, and, starting at any key, counting seven keys to the right (both black and white) to get to the next note on the circle shown above. Seven half steps, the distance from the 1st to the 8th key on a piano is a "perfect fifth", called 'perfect' because it is neither major nor minor, but applies to both major and minor scales and chords, and a 'fifth' because though it is a distance of seven semitones on a keyboard, it is a distance of five steps within a major or minor scale.
A simple way to hear the relationship between these notes is by playing them on a piano keyboard. If you traverse the circle of fifths backwards, the notes will feel as though they fall into each other. This aural relationship is what the mathematics describes.[citation needed]
Perfect fifths may be justly tuned or tempered. Two notes whose frequencies differ by a ratio of 3:2 make the interval known as a justly tuned perfect fifth. Cascading twelve such fifths does not return to the original pitch class after going round the circle, so the 3:2 ratio may be slightly detuned, or tempered. Temperament allows perfect fifths to cycle, and allows pieces to be transposed, or played in any key on a piano or other fixed-pitch instrument without distorting their harmony. The primary tuning system used for Western (especially keyboard and fretted) instruments today is called twelve-tone equal temperament.
[edit] History
| This section requires expansion. |
The earliest known description of the circle of fifths is in Nikolay Diletsky's 1679 composition treatise, Grammatika musikiyskago peniya (A Grammar of Music[al Singing]).[7] Johann David Heinichen independently described it in his 1711 treatise, Neu erfundene und gründliche Anweisung.[8]
[edit] Related concepts
[edit] Diatonic circle of fifths
The diatonic circle of fifths is the circle of fifths encompassing only members of the diatonic scale. As such it contains a diminished fifth, in C major between B and F. See structure implies multiplicity.
The circle progression is commonly a circle through the diatonic chords by fifths, including one diminished chord and one progression by diminished fifth:

[edit] Chromatic circle
The circle of fifths is closely related to the chromatic circle, which also arranges the twelve equal-tempered pitch classes in a circular ordering. A key difference between the two circles is that the chromatic circle can be understood as a continuous space where every point on the circle corresponds to a conceivable pitch class, and every conceivable pitch class corresponds to a point on the circle. By contrast, the circle of fifths is fundamentally a discrete structure, and there is no obvious way to assign pitch classes to each of its points. In this sense, the two circles are mathematically quite different.
However, the twelve equal-tempered pitch classes can be represented by the cyclic group of order twelve, or equivalently, the residue classes modulo twelve, 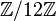 . The group
. The group 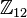 has four generators, which can be identified with the ascending and descending semitones and the ascending and descending perfect fifths. The semitonal generator gives rise to the chromatic circle while the perfect fifth gives rise to the circle of fifths.
has four generators, which can be identified with the ascending and descending semitones and the ascending and descending perfect fifths. The semitonal generator gives rise to the chromatic circle while the perfect fifth gives rise to the circle of fifths.
[edit] Relation with chromatic scale
The circle of fifths, or fourths, may be mapped from the chromatic scale by multiplication, and vice versa. To map between the circle of fifths and the chromatic scale (in integer notation) multiply by 7 (M7), and for the circle of fourths multiply by 5 (P5).
Here is a demonstration of this procedure. Start off with an ordered 12-tuple (tone row) of integers
- (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)
representing the notes of the chromatic scale: 0 = C, 2 = D, 4 = E, 5 = F, 7 = G, 9 = A, 11 = B, 1 = C♯, 3 = D♯, 6 = F♯, 8 = G♯, 10 = A♯. Now multiply the entire 12-tuple by 7:
- (0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)
and then apply a modulo 12 reduction to each of the numbers (subtract 12 from each number as many times as necessary until the number becomes smaller than 12):
- (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)
which is equivalent to
- (C, G, D, A, E, B, F♯, C♯, G♯, D♯, A♯, F)
which is the circle of fifths. Note that this is enharmonically equivalent to:
- (C, G, D, A, E, B, G♭, D♭, A♭, E♭, B♭, F)
[edit] Infinite series
The “bottom keys” of the circle of fifths are often written in flats and sharps, as they are easily interchanged using enharmonics. For example, the key of B, with five sharps, is enharmonically equivalent to the key of C♭, with 7 flats. But the circle of fifths doesn’t stop at 7 sharps (C♯) or 7 flats (C♭). Following the same pattern, one can construct a circle of fifths with all sharp keys, or all flat keys.
After C♯ comes the key of G♯ (following the pattern of being a fifth higher, and, coincidentally, enharmonically equivalent to the key of A♭). The “8th sharp” is placed on the F♯, to make it F![]() . The key of D♯, with 9 sharps, has another sharp placed on the C♯, making it C
. The key of D♯, with 9 sharps, has another sharp placed on the C♯, making it C![]() . The same for key signatures with flats is true; The key of E (four sharps) is equivalent to the key of F♭ (again, one fifth below the key of C♭, following the pattern of flat key signatures. The double-flat is placed on the B♭, making it B
. The same for key signatures with flats is true; The key of E (four sharps) is equivalent to the key of F♭ (again, one fifth below the key of C♭, following the pattern of flat key signatures. The double-flat is placed on the B♭, making it B![]() .)
.)
[edit] See also
- Array system
- Cadence (music)
- Chord progression
- Chromatic circle
- Diatonic function
- Enharmonic
- Pythagorean comma
- Sonata form
- Well temperament
[edit] Notes
- ^ Nattiez (1990).
- ^ Goldman (1965), p.68.
- ^ Goldman, ibid., chapter 3
- ^ Nattiez (1990), p. 226.
- ^ Goldman (1968), p.68.
- ^ Nattiez (1990), p.226.
- ^ Jensen.
- ^ Lester discusses the history in detail.
- ^ "Prelude to Musical Geometry", p.364, Brian J. McCartin, The College Mathematics Journal, Vol. 29, No. 5 (Nov., 1998), pp. 354-370. (abstract) (JSTOR)
[edit] References
- D'Indy (1903). Cited in Nattiez (1990).
- Goldman (1965). Harmony in Western Music. Cited in Nattiez (1990).
- Jensen, Claudia R. A Theoretical Work of Late Seventeenth-Century Muscovy: Nikolai Diletskii's "Grammatika" and the Earliest Circle of Fifths. Journal of the American Musicological Society, Vol. 45, No. 2 (Summer, 1992), pp. 305-331.
- Lester, Joel. Between Modes and Keys: German Theory, 1592-1802. 1990.
- Nattiez, Jean-Jacques (1990). Music and Discourse: Toward a Semiology of Music (Musicologie générale et sémiologue, 1987). Translated by Carolyn Abbate (1990). ISBN 0691027145.
[edit] Further reading
- Miller, Michael. The Complete Idiot's Guide to Music Theory, 2nd ed. [Indianapolis, IN]: Alpha, 2005. ISBN 1592574378.
[edit] External links
- Circle of Fifths Memory Technique
- circleoffifths.com Poster
- Interactive Circle of Fifths
- Bach's Tuning by Bradley Lehman
- mnemonics
- Circle of Fifths - Diagram
- Circle of Fifths - In Bass Clef
- How to Improvise Around the Circle of Fifths Video explaining the circle of fifths and how to use it to improvise with
- Major Keys: How to use the Circle of Fifths A video showing how to use the Circle of Fifths for Major Keys
- Minor Keys: How to use the Circle of Fifths A video showing how to use the Circle of Fifths for Minor Keys









