An Exceptionally Simple Theory of Everything
From Wikipedia, the free encyclopedia
An Exceptionally Simple Theory of Everything is a preprint proposing a basis for a unified field theory, named E8 Theory,[1] which attempts to describe all known fundamental interactions in physics, and to stand as a possible theory of everything. The preprint was posted to the physics arXiv by Antony Garrett Lisi in November 2007,[2] and has not been published in a formally peer-reviewed scientific journal. The title is a pun on the algebra used, the Lie algebra of the largest "simple," "exceptional" Lie group, E8.
The theory "received accolades from a few physicists amid a flurry of media coverage," but also "widespread skepticism."[3] Scientific American reported in March 2008 that the theory was being "largely but not entirely ignored" by the mainstream physics community, with a few physicists picking up the work to develop it further.[4] Next to some citations,[5] it quickly became the most downloaded article in the arXiv.[6]
Contents |
[edit] Overview
Lisi's model[2] is a variant and extension of a Grand Unification Theory (a "GUT," describing electromagnetism, the weak interaction and the strong interaction) to include gravitation, a Higgs boson and fermions in an attempt to describe all fields of the Standard Model and gravity as different parts of one field over four dimensional spacetime. More specifically, Lisi combines the left-right symmetric Pati-Salam GUT with a MacDowell-Mansouri description of gravity, using the spin connection and gravitational frame combined with a Higgs boson, necessitating a cosmological constant. The model is formulated as a gauge theory, using a modified BF action, with E8 as the Lie group. Mathematically, this is an E8 principal bundle, with connection, over a four dimensional base manifold. Lisi's embedding of the Standard Model gauge group in E8 leads him to predict the existence of 22 new bosonic particles at an undetermined mass scale.
The fermions enter, via an unconventional use of the BRST technique, as Grassmann number fields valued in part of the E8 Lie algebra. The bosons are combined with these fermions as one-form and Grassmann number parts of a sort of superconnection, each valued in separate parts of the E8 Lie algebra. The curvature of this superconnection is calculated, producing the Riemann curvature, gauge field curvature, gravitational torsion, covariant derivative of the Higgs, and the covariant Dirac derivative of the fermions. This curvature is used to build the modified BF action by hand, in an attempt to match the dynamics of the Standard Model and gravity.
In the paper, Lisi describes several deficiencies in this model. The most important deficiency is noted as an incorrect, or "poorly understood," inclusion of the second and third generations of fermions in E8, relying on triality. This deficiency, and the incomplete nature of the model, prevents the prediction of masses for new or existing particles. Also, Lisi notes the use of explicit symmetry breaking in building his action, rather than offering a more desirable spontaneous symmetry breaking mechanism. And, no attempt is made to provide a quantum description of the theory—this being left for future work.
In a follow-up paper,[7] Lee Smolin proposes a spontaneous symmetry breaking mechanism for obtaining the action in Lisi's model, and speculates on the path to its quantization as a spin foam.
[edit] Non-technical overview
Consider a wavy, two-dimensional surface, with many different spheres glued to the surface—one sphere at each surface point, and each sphere attached by one point. This geometric construction is a fiber bundle, with the spheres as the "fibers," and the wavy surface as the "base." A sphere can be rotated in three different ways: around the x-axis, the y-axis, or around the z-axis. Each of these rotations corresponds to a symmetry of the sphere. The fiber bundle connection is a field describing how spheres at nearby surface points are related, in terms of these three different rotations. The geometry of the fiber bundle is described by the curvature of this connection. In the corresponding quantum field theory, there is a particle associated with each of these three symmetries, and these particles can interact according to the geometry of a sphere.
In Lisi's model, the base is a four-dimensional surface—our spacetime—and the fiber is the E8 Lie group, a complicated 248 dimensional shape, which some mathematicians consider to be the most beautiful shape in mathematics.[8] In this theory, each of the 248 symmetries of E8 corresponds to a different elementary particle, which can interact according to the geometry of E8. As Lisi describes it: "The principal bundle connection and its curvature describe how the E8 manifold twists and turns over spacetime, reproducing all known fields and dynamics through pure geometry."[2]
The complicated geometry of the E8 Lie group is described graphically using group representation theory. Using this mathematical description, each symmetry of a group—and so each kind of elementary particle—can be associated with a point in a diagram. The coordinates of these points are the quantum numbers—the charges—of elementary particles, which are conserved in interactions. Such a diagram sits in a flat, Euclidean space of some dimension, forming a polytope, such as the 421 polytope in eight-dimensional space.
In order to form a theory of everything, Lisi's model must eventually predict the exact number of fundamental particles, all of their properties, masses, forces between them, the nature of spacetime, and the cosmological constant. Much of this work is still in the conceptual stage—in particular, quantization and predictions of particle masses have not been done. And Lisi himself acknowledges it as a work-in-progress: "The theory is very young, and still in development."[9]
[edit] Description
Lisi's model attempts to describe all known fields—the gravitational spin connection, frame, Higgs, gauge bosons, and three generations of fermions—as different parts of a single superconnection over a four-dimensional base manifold.
[edit] Superconnection
Lisi's superconnection is built by formally adding a connection 1-form field to a Grassmann number 0-form field, both valued in different parts of a Lie algebra,  ,[2][10]
,[2][10]

The bosonic part of the superconnection,  , is valued in a reductive subalgebra,
, is valued in a reductive subalgebra,  , of
, of  , i.e. satisfying the Lie bracket relations,
, i.e. satisfying the Lie bracket relations,
![[ \mathfrak{h}, \mathfrak{h} ] = \mathfrak{h}](http://upload.wikimedia.org/math/7/6/c/76c42d6d476d4ce2e47d8b1e312970bd.png)
![[ \mathfrak{h}, \mathfrak{k} ] = \mathfrak{k}](http://upload.wikimedia.org/math/c/b/b/cbba1e00dbd1a9a729a8c5f5780f8c72.png)
The fermionic part of the superconnection,  , is valued in the remainder of the Lie algebra,
, is valued in the remainder of the Lie algebra,  . Lisi states this superconnection is a kind of "BRST extended connection," in which the
. Lisi states this superconnection is a kind of "BRST extended connection," in which the 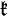 valued part of a 1-form connection has been replaced by BRST ghosts valued in
valued part of a 1-form connection has been replaced by BRST ghosts valued in 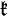 . In Lisi's model the relevant Lie algebra is the split real form of
. In Lisi's model the relevant Lie algebra is the split real form of  and the bosonic subalgebra is[11][10]
and the bosonic subalgebra is[11][10]

[edit] Algebraic breakdown
Lisi proposes a decomposition of e8, the 248 dimensional Lie algebra of E8, into parts accommodating the gravitational and standard model fields according to the following schema:[2][12][11][10]
|
|
|
|
|
|
|
|
|
|
|
|
|
ToE e8  |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
graviweak  |
|
|
|
|
|
|
strong B-L  |
|
|
|
|
|
|
fermions  |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
gravity  |
frame-Higgs  |
electroweak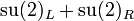  |
strong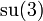  |
B-L  |
new bosons 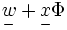 |
gen 1  |
gen 2  |
gen 3  |
|||||||||||||||||||||||||||||||||||||||||||||
Under this decomposition, Lisi's e8 valued superconnection for everything is
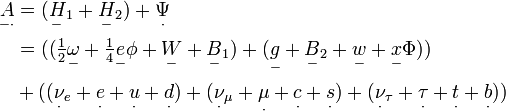
in which  is the spin connection,
is the spin connection,  is the gravitational frame,
is the gravitational frame,  is the Higgs boson,
is the Higgs boson, 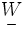 is a weak gauge field,
is a weak gauge field,  is the right partner to the weak gauge field,
is the right partner to the weak gauge field,  is the strong gauge field,
is the strong gauge field,  is the baryon minus lepton number gauge field,
is the baryon minus lepton number gauge field, 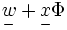 are new gauge bosons, and the rest of the fields are the standard model fermions. Lisi's detailed description of the spin connection, frame-Higgs and fermions, as parts of e8, relies heavily on the Clifford algebra Cℓ7, 1(R).[2] Lisi says this left-right symmetric model, similar to the Pati-Salam model, must be broken to obtain the standard model. Notably, Lisi includes fermions along with bosons in the same representation, and also proposes tentatively that the three generations of fermions of the standard model may be described by a triality rotation (relating to the three-fold symmetry of SO(8)). He notes that the second and third generations of fermions do not obviously have the correct quantum numbers in this model—and that this stands as the least understood aspect of the theory, and the largest outstanding problem.
are new gauge bosons, and the rest of the fields are the standard model fermions. Lisi's detailed description of the spin connection, frame-Higgs and fermions, as parts of e8, relies heavily on the Clifford algebra Cℓ7, 1(R).[2] Lisi says this left-right symmetric model, similar to the Pati-Salam model, must be broken to obtain the standard model. Notably, Lisi includes fermions along with bosons in the same representation, and also proposes tentatively that the three generations of fermions of the standard model may be described by a triality rotation (relating to the three-fold symmetry of SO(8)). He notes that the second and third generations of fermions do not obviously have the correct quantum numbers in this model—and that this stands as the least understood aspect of the theory, and the largest outstanding problem.
[edit] Visual representation
The algebraic structure of the standard model and gravitational fields may be described using group representation theory, with roots and weights corresponding to the charge quantum numbers of elementary particle states. Different kinds of charge correspond to the different fundamental forces, with weak hypercharge and weak isospin of the electroweak force combining to produce electric charge, and two kinds of charge quantum numbers associated with the color charge of the strong force. These four kinds of standard model charge are conserved in all elementary particle interactions. In Lisi's theory, the spin of elementary particles are the charges with respect to the gravitational force, with a different spin charge for the left and right chiral parts of the gravitational spin connection. The quantum numbers of all elementary particles is a pattern of points in six dimensional charge space, which may be projected down to two dimensions and plotted, creating a visual representation of the algebraic structure. In Lisi's E8 Theory these charges in six dimensions are a projection of some of the E8 root system in eight charge dimensions. The standard model or E8 system of charges and allowed particle interactions may be rotated in eight dimensions and visualized via an online tool, the Elementary Particle Explorer.[13]
[edit] Curvature
The dynamics in Lisi's model depends on the supercurvature of the superconnection,[2][10]
![\begin{align}
\underset{=\cdot}{F} & = \underset{-}{d} \underset{-\cdot}{A} + \tfrac{1}{2} [ \underset{-\cdot}{A}, \underset{-\cdot}{A} ] \\
& = \underset{-}{d} (\underset{-}{H}+\underset{\cdot}{\Psi}) + \tfrac{1}{2} [ (\underset{-}{H}+\underset{\cdot}{\Psi}), (\underset{-}{H}+\underset{\cdot}{\Psi}) ] \\
& = (\underset{-}{d} \underset{-}{H} + \tfrac{1}{2} [ \underset{-}{H}, \underset{-}{H} ] )
+ (\underset{-}{d} \underset{\cdot}{\Psi} + [ \underset{-}{H},\underset{\cdot}{\Psi}) ] )
+ ( \tfrac{1}{2} [ \underset{\cdot}{\Psi}, \underset{\cdot}{\Psi} ] ) \\
& = \underset{=}{F} + \underset{-}{D} \underset{\cdot}{\Psi} + \underset{\cdot}{\Psi} \underset{\cdot}{\Psi}
\end{align}](http://upload.wikimedia.org/math/6/0/5/605528ee51c93909ad13ffc408b9e4c2.png)
in which  is the bosonic curvature form and
is the bosonic curvature form and  is the exterior covariant derivative of the fermions. Under Lisi's algebraic breakdown of e8, the supercurvature decomposes into parts,[2]
is the exterior covariant derivative of the fermions. Under Lisi's algebraic breakdown of e8, the supercurvature decomposes into parts,[2]
|
|
|
|
|
|
|
|
|
|
|
|
|
ToE e8  |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
graviweak  |
|
|
|
|
|
|
strong B-L  |
|
|
|
|
|
|
fermions  |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
gravity  |
frame-Higgs  |
electroweak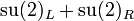  |
strong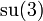  |
B-L  |
new bosons  |
gen 1  |
gen 2  |
gen 3 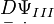 |
|||||||||||||||||||||||||||||||||||||||||||||
in which  is the Riemann curvature 2-form,
is the Riemann curvature 2-form, ![\underset{=}{T}=\underset{-}{d} \underset{-}{e} + \tfrac{1}{2} [\underset{-}{\omega},\underset{-}{e}]](http://upload.wikimedia.org/math/5/1/f/51f4dfba1bfca5f4ba84e2121e496b6f.png) is the torsion 2-form, and
is the torsion 2-form, and  is the massive covariant derivative of the fermions, as Dirac spinors, in curved spacetime.
is the massive covariant derivative of the fermions, as Dirac spinors, in curved spacetime.
[edit] Action
To specify dynamics matching general relativity and the standard model, Lisi postulates a modified BF theory action,

producing the Einstein-Hilbert action for gravity, the Yang-Mills action for gauge fields, the action for the Higgs boson, and the action for fermions in curved spacetime. The cosmological constant in Lisi's model is necessarily related to the vacuum expectation value of the Higgs, 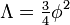 .
.
It should be noted that this action breaks the E8 symmetry by hand. However, Lee Smolin has proposed a way to obtain the bosonic part of Lisi's action (plus higher-order terms) from a fully E8-symmetric theory, by starting with the action:[7]
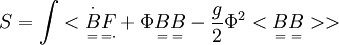
[edit] Vector-form notation
Lisi employs an unusual mathematical notation in his work with vectors and differential forms.[2] He denotes the grade of a differential form by underlines, as in the curvature 2-form,

in which he does not write the wedge—taking the coordinate basis 1-forms to always anti-commute. For the interior product between a vector, 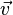 , and a form, Lisi writes
, and a form, Lisi writes

taking the coordinate basis vectors and their dual coordinate basis 1-forms to contract as  . This is similar to Dirac's Bra-ket notation for vectors in Hilbert space, and Lisi uses the order-dependent nature of this contraction to describe vector valued forms similar to "ket-bra"'s, such as
. This is similar to Dirac's Bra-ket notation for vectors in Hilbert space, and Lisi uses the order-dependent nature of this contraction to describe vector valued forms similar to "ket-bra"'s, such as

Also, Lisi uses an under-dot, as in  , to denote the Grassmann grade of a field.
, to denote the Grassmann grade of a field.
[edit] Predictions
By matching 226 known standard model particles to some of the 248 symmetries of E8, Lisi is able to predict the existence and quantum numbers of 22 new particles.[2] Three of these, the  and
and  , are the same new
, are the same new  and
and  gauge bosons as predicted in the Pati-Salam model, the W' and Z' bosons. Another, the
gauge bosons as predicted in the Pati-Salam model, the W' and Z' bosons. Another, the 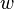 , is a new
, is a new  gauge boson, with a corresponding new quantum number. And the remaining 18 new bosons predicted, the
gauge boson, with a corresponding new quantum number. And the remaining 18 new bosons predicted, the  , are new colored fields, interacting with the strong force. Lisi states that some of these 22 particles might be seen at the Large Hadron Collider.[14]
, are new colored fields, interacting with the strong force. Lisi states that some of these 22 particles might be seen at the Large Hadron Collider.[14]
It is important to note that Lisi does not specify masses for these predicted particles. This implies these predictions are not falsifiable, because the masses can always be speculated to be beyond the reach of a given experiment. However, the discovery of new particles that do not fit in Lisi's classification, such as superpartners, would fall outside the model, and falsify Lisi's match to E8. Also, because the matching of the three fermion generations is tentative and problematic in the model, Lisi places a low confidence in these predictions.
[edit] Chronology and reaction
Three previous arXiv preprints by Lisi dealt with related questions. "Clifford Geometrodynamics" in 2002,[15] "Clifford bundle formulation of BF gravity generalized to the standard model" in 2005,[16] and "Quantum mechanics from a universal action reservoir," in 2006.[17] Lisi further discussed his work on an FQXi forum in 2007,[18] at an FQXi conference,[19] and in an FQXi article.[1] He also gave talks at the Loops '07 conference in Morelia, Mexico[20] and the Perimeter Institute.[21] Commentary on his work was found in John Baez's "This Week's Finds in Mathematical Physics (Week 253),"[22] and he is interviewed on Sabine Hossenfelder "Backreaction" blog.[23] Lisi's arXiv preprint An Exceptionally Simple Theory of Everything appeared on 6 November 2007, where Lisi describes how gravity, the standard model bosons, and three generations of fermions can be unified using an E8 superconnection.[2]
Lisi's paper attracted a great deal of attention after its release and spun-off a variety of debates across various blogs and online discussion groups. Numerous news sites from all over the world reported this new theory, noting the personal background of Lisi, and the controversy in the physics community surrounding the preprint. Mainstream and scientific press coverage included: The Daily Telegraph (14 November 2007),[9] New Scientist (15 November 2007),[24] Wired News (16 November 2007),[25] Le Monde (19 November 2007),[26] The Economist (22 November 2007),[27] The Daily Telegraph (22 January 2008),[28] Discover Magazine (26 February 2008),[29] Wired Magazine (27 February 2008),[30] Scientific American (1 March 2008),[4] Physics World (1 July 2008),[31] and The New Yorker (21 July 2008).[32]
Numerous blogs and forums also discussed the work including Sabine Hossenfelder's Backreaction,[33] Luboš Motl's The Reference Frame, which objects to the addition of bosons and fermions in Lisi's superconnection, and to the violation of the Coleman-Mandula theorem,[34] Peter Woit's Not Even Wrong,[35] Sean Carroll's Cosmic Variance,[36] Steinn Sigurðsson's Dynamics of Cats,[37] Physics Forums[38] Slashdot,[39]Digg,[40] and Reddit.[41] Woit, Smolin are generally supportive whereas Motl and Marcus du Sautoy are critical.
Jacques Distler's Musings is one of the strongest criticisms of Lisi's approach, claiming to demonstrate that, unlike the Standard Model, Lisi's model is nonchiral[42] — consisting of a generation and an anti-generation — and to prove that any alternative embedding in E8 must be similarly nonchiral.[12][43] The group blog, The n-Category Cafe, provides some of the more technical discussions with posts by Lisi, Urs Schreiber,[10] Kea,[44] and Jaques Distler.[44]
Lisi has made further presentations at International Loop Quantum Gravity Seminar on 13 November 2007[45] and responded to press enquiries on an FQXi forum in 20 November 2007[46] He presented his work at the TED Conference on 28 February 2008.[47]
Several arXiv preprints build on Lisi's work: Lee Smolin "The Plebanski action extended to a unification of gravity and Yang-Mills theory," 6 December 2007, proposes a symmetry breaking mechanism to go from an E8 symmetric action to Lisi's action for the standard model and gravity.[7] Roberto Percacci "Mixing internal and spacetime transformations: some examples and counterexamples",[48] and Bertram Kostant discusses in a colloquium presentation at UC Riverside.[49]
In the presentation "What's new at the arXiv?" on 20 May 2008, Simeon Warner stated that Lisi's paper is the most downloaded article on the arXiv.[6][50]
FQXi awarded Lisi a grant for further development of "E8 Theory" on 4 August 2008.[51][52]
[edit] References
- ^ a b Scott Dodd (2007-10-26). "= /community/data/articles/Lisi_Garrett.pdf Surfing the Folds of Spacetime" (PDF). FQXi article. http://fqxi.org/community/download.php?url = /community/data/articles/Lisi_Garrett.pdf. Retrieved on 2008-06-15.
- ^ a b c d e f g h i j k A. G. Lisi (2007). "An Exceptionally Simple Theory of Everything". arΧiv: 0711.0770.
- ^ Amber Dance (2008-04-01). "Outsider Science". Symmetry Magazine. http://www.symmetrymagazine.org/cms/?pid=1000607. Retrieved on 2008-06-15.
- ^ a b Collins, Graham P. (March 2008). ""Wipeout?"". Scientific American: 30–32. http://www.sciam.com/article.cfm?id=wipeout-theory. Retrieved on 2008-06-18.
- ^ "Citations for 0711.0770". arXiv. 2007-06-20. http://arxiv.org/cits/0711.0770. Retrieved on 2008-10-19.
- ^ a b Simeon Warner (2008-05-20). "What's new at the arXiv?". HEP Information Resource Summit. http://indico.desy.de/conferenceOtherViews.py?confId=800#2008-05-20. Retrieved on 2008-07-22. (The slide containing this statement was subsequently removed from the presentation file.)
- ^ a b c Lee Smolin (2007). "The Plebanski action extended to a unification of gravity and Yang-Mills theory". arΧiv: 0712.0977.
- ^ "Mathematicians Map E8". AIM. http://www.aimath.org/E8/. Retrieved on 2007-12-30.
- ^ a b Roger Highfield (2007-11-14). "Surfer dude stuns physicists with theory of everything". The Daily Telegraph. http://www.telegraph.co.uk/earth/main.jhtml?view=DETAILS&grid=&xml=/earth/2007/11/14/scisurf114.xml. Retrieved on 2008-06-15.
- ^ a b c d e Urs Schreiber (2008-05-10). "E8 Quillen Superconnection". The n-Category Cafe. http://golem.ph.utexas.edu/category/2008/05/e8_quillen_superconnection.html. Retrieved on 2008-06-15.
- ^ a b Jacques Distler (2007-12-09). "A Little More Group Theory". Musings. http://golem.ph.utexas.edu/~distler/blog/archives/001532.html. Retrieved on 2008-08-30.
- ^ a b Jacques Distler (2007-11-21). "A Little Group Theory". Musings. http://golem.ph.utexas.edu/~distler/blog/archives/001505.html. Retrieved on 2008-06-15.
- ^ Troy Gardner (2008-08-09). "Elementary Particle Explorer". Deferential Geometry. http://deferentialgeometry.org/epe/. Retrieved on 2008-09-04.
- ^ "The Big Bang: what will we find?". The Daily Telegraph. 2008-03-25. http://www.telegraph.co.uk/earth/main.jhtml?xml=/earth/2008/03/25/scicomments125.xml. Retrieved on 2008-06-15.
- ^ A. G. Lisi (2002). "Clifford Geometrodynamics". arΧiv: gr-qc/0212041.
- ^ A. G. Lisi (2005). "Clifford bundle formulation of BF gravity generalized to the standard model". arΧiv: gr-qc/0511120.
- ^ A. G. Lisi (2006). "Quantum mechanics from a universal action reservoir". arΧiv: physics/0605068.
- ^ A. G. Lisi (2007-06-09). "Pieces of E8". FQXi forum. http://fqxi.org/community/forum/topic/68. Retrieved on 2008-06-15.
- ^ A. G. Lisi (2007-07-21). "Standard model and gravity". inaugural FQXi conference. http://fqxi.org/conference/talkslides.html. Retrieved on 2008-06-15.
- ^ A. G. Lisi (2007-06-25). "Deferential Geometry". Loops '07 conference. http://www.matmor.unam.mx/eventos/loops07/cont_abs.html#lisi. Retrieved on 2008-06-15.
- ^ A. G. Lisi (2007-10-04). "An Exceptionally Simple Theory of Everything". Perimeter Institute talk. http://pirsa.org/07100001. Retrieved on 2008-06-15.
- ^ John Baez (2007-06-27). "This Week's Finds in Mathematical Physics (Week 253)". http://math.ucr.edu/home/baez/week253.html. Retrieved on 2008-06-15.
- ^ Sabine Hossenfelder (2007-08-06). "Garrett Lisi's Inspiration". Backreaction. http://backreaction.blogspot.com/2007/08/garrett-lisis-inspiration.html. Retrieved on 2008-06-15.
- ^ Zeeya Merali (2007-11-15). "Is mathematical pattern the theory of everything?". New Scientist. http://www.newscientist.com/channel/fundamentals/dn12891-is-mathematical-pattern-the-theory-of-everything.html. Retrieved on 2008-06-15.
- ^ John Borland (2007-11-16). "Surfer-Physicist Offers A New Way To Explain Everything". Wired News. http://blog.wired.com/wiredscience/2007/11/surfer-physicis.html. Retrieved on 2008-06-15.
- ^ Stéphane Foucart (2007-11-19). "= ARCHIVES&type_item=ART_ARCH_30J&objet_id=1013839&clef=ARC-TRK-D_01 The theory is mathematically and aesthetically superb". Le Monde. http://www.lemonde.fr/cgi-bin/ACHATS/acheter.cgi?offre = ARCHIVES&type_item=ART_ARCH_30J&objet_id=1013839&clef=ARC-TRK-D_01. Retrieved on 2008-06-16.
- ^ "Geometry is all". The Economist. 2007-11-22. http://www.economist.com/science/displaystory.cfm?story_id=10170958. Retrieved on 2008-06-15.
- ^ Marcus du Sautoy (2008-01-22). "Garrett Lisi: This surfer is no Einstein...". The Daily Telegraph. http://www.telegraph.co.uk/earth/main.jhtml?xml=/earth/2008/01/22/scieinstein122.xml. Retrieved on 2008-06-15.
- ^ "Could the Next Einstein Be a Surfer Dude?". Discover Magazine. 2008-02-26. http://discovermagazine.com/2008/mar/13-e-nste-n. Retrieved on 2008-06-15.
- ^ Kim Zetter (2008-02-27). "Surfer-Physicist's Unified Theory Leads to Fame, Backlash". Wired Magazine. http://www.wired.com/science/discoveries/news/2008/02/ted_lisi. Retrieved on 2008-06-15.
- ^ Stephen Maxfield (2008-07-01). "Symmetry's physical dimension". Physics World. http://physicsworld.com/cws/article/print/34784. Retrieved on 2008-07-10.
- ^ Benjamin Wallace-Wells (2008-07-21). "Surfing the Universe". The New Yorker. http://www.newyorker.com/reporting/2008/07/21/080721fa_fact_wallacewells.
- ^ Sabine Hossenfelder (2007-11-06). "A Theoretically Simple Exception of Everything". Backreaction. http://backreaction.blogspot.com/2007/11/theoretically-simple-exception-of.html. Retrieved on 2008-06-15.
- ^ Luboš Motl (2007-11-07). "Garrett Lisi: An exceptionally simple theory of everything". The Reference Frame. http://motls.blogspot.com/2007/11/exceptionally-simple-theory-of.html. Retrieved on 2008-06-15.
- ^ Peter Woit (2007-11-09). "An Exceptionally Simple Theory of Everything?". Not Even Wrong. http://www.math.columbia.edu/~woit/wordpress/?p=617. Retrieved on 2008-06-15.
- ^ Sean Carroll (2007-11-16). "Garrett Lisi’s Theory of Everything!". Cosmic Variance. http://cosmicvariance.com/2007/11/16/garrett-lisis-theory-of-everything/. Retrieved on 2008-06-15.
- ^ Steinn Sigurðsson (2007-11-20). "red boson, blue fermion". Dynamics of Cats. http://scienceblogs.com/catdynamics/2007/11/red_boson_blue_fermion.php. Retrieved on 2008-06-16.
- ^ "An Exceptionally Simple Theory of Everything!". Physics Forums. 2007-11-06. http://www.physicsforums.com/showthread.php?t=196498. Retrieved on 2008-06-15.,
- ^ "A New Theory of Everything?". Slashdot. 2007-11-15. http://science.slashdot.org/article.pl?sid=07/11/15/2322225. Retrieved on 2008-06-15.
- ^ "Surfer Dude Stuns Physicists With Theory of Everything". Digg. 2007-11-15. http://digg.com/general_sciences/Surfer_Dude_Stuns_Physicists_With_Theory_of_Everything_2. Retrieved on 2008-06-16.
- ^ "Surfer dude stuns physicists with theory of everything". Reddit. 2007-11-15. http://www.reddit.com/info/60msi/comments/. Retrieved on 2008-06-15.
- ^ Jacques Distler (2007-12-09). "A Little More Group Theory". Musings. http://golem.ph.utexas.edu/~distler/blog/archives/001532.html. Retrieved on 2008-11-15.
- ^ Jacques Distler (2008-09-14). "My Dinner with Garrett". Musings. http://golem.ph.utexas.edu/~distler/blog/archives/001795.html. Retrieved on 2008-11-15.
- ^ a b http://golem.ph.utexas.edu/category/2008/05/e8_quillen_superconnection.html#c016877
- ^ A. G. Lisi (2007-11-13). "A Connection With Everything". International Loop Quantum Gravity Seminar. http://relativity.phys.lsu.edu/ilqgs/. Retrieved on 2008-06-15.
- ^ A. G. Lisi (2007-11-20). "An Exceptionally Simple FAQ". FQXi forum. http://fqxi.org/community/forum/topic/107. Retrieved on 2008-06-15.
- ^ A. G. Lisi (2008-02-28). "Garrett Lisi: A beautiful new theory of everything". TED talks. http://www.ted.com/index.php/speakers/garrett_lisi.html. Retrieved on 2008-10-17.
- ^ Roberto Percacci (2008). "Mixing internal and spacetime transformations: some examples and counterexamples". arΧiv: 0803.0303.
- ^ Bertram Kostant (2008-02-12). "On Some Mathematics in Garrett Lisi's 'E8 Theory of Everything'". UC Riverside mathematics colloquium. http://math.ucr.edu/home/baez/kostant/. Retrieved on 2008-06-15.
- ^ Peter Woit (2008-05-28). "INSPIRE". Not Even Wrong. http://www.math.columbia.edu/~woit/wordpress/?p=693. Retrieved on 2008-08-05.
- ^ "E8 Theory". FQXi. 2008-08-04. http://www.fqxi.org/large-grants/awardee/details/2008/lisi. Retrieved on 2008-08-05.
- ^ "FQXi Grants". FQXi. http://www.fqxi.org/grants. Retrieved on 2008-08-08.
[edit] External links
- Deferential Geometry - Lisi's wiki, containing detailed mathematical background.
- Animation of E8 - a New Scientist video describing the theory using a visual representation.
- The Elementary Particle Explorer - an online E8 investigation tool for rotating and examining the particle assignments, charges, and interactions in the standard model and Lisi's E8 Theory.
- E8Flyer - An interactive E8 investigation tool based on the free Mathematica Notebook Player) (* see [1] for screen shots *)
- An Exceptionally Technical Discussion of AESToE - a thread at "Physics Forums," started by Garrett Lisi, devoted to discussing the mathematics used in the AESToE paper.
- A beautiful new theory of everything - Lisi presents his theory at TED.
|
|||||||||


