Kernel density estimation

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Kernel density estimation of 100 normally distributed random numbers using different smoothing bandwidths.

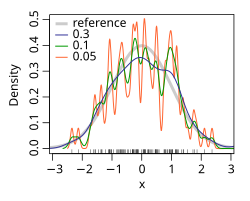
In statistics, kernel density estimation (or Parzen window method, named after Emanuel Parzen) is a non-parametric way of estimating the probability density function of a random variable. As an illustration, given some data about a sample of a population, kernel density estimation makes it possible to extrapolate the data to the entire population.

The Parzen window is also used in signal processing as a lag window, in such procedures as the Blackman-Tukey procedure.

A histogram can be thought of as a collection of point samples from a kernel density estimate for which the kernel is a uniform box the width of the histogram bin.

Contents

[edit] Definition

If x1, x2, ..., xN ~ ƒ is an independent and identically-distributed sample of a random variable, then the kernel density approximation of its probability density function is

\widehat{f}_h(x)=\frac{1}{Nh}\sum_{i=1}^N K\left(\frac{x-x_i}{h}\right)

where K is some kernel and h is a smoothing parameter called the bandwidth. Quite often K is taken to be a standard Gaussian function with mean zero and variance 1:[dubious – discuss]

K(x) = {1 \over \sqrt{2\pi} }\,e^{-\frac{1}{2}x^2}.

[edit] Intuition

Although less smooth density estimators such as the histogram density estimator can be made to be asymptotically consistent, others are often either discontinuous or converge at slower rates than the kernel density estimator. Rather than grouping observations together in bins, the kernel density estimator can be thought to place small "bumps" at each observation, determined by the kernel function. The estimator consists of a "sum of bumps" and is clearly smoother as a result (see below image).

Six Gaussians (red) and their sum (blue). The Parzen window density estimate f(x) is obtained by dividing this sum by 6, the number of Gaussians. The variance of the Gaussians was set to 0.5. Note that where the points are denser the density estimate will have higher values.

[edit] Properties

Let \scriptstyle R(f,\hat f(x)) be the L2 risk function for ƒ. Under weak assumptions on ƒ and K,

R(f,\hat f(x)) \approx \frac{1}{4}\sigma_k^4h^4\int(f''(x))^2\,dx + \frac{\int K^2(x)\,dx}{nh}\text{ where }\sigma_K^2 = \int x^2K(x)\,dx.

By minimizing the theoretical risk function, it can be shown that the optimal bandwidth is

h^* = \frac{c_1^{-2/5}c_2^{1/5}c_3^{-1/5}}{n^{1/5}}

where

c_1 = \int x^2K(x)\,dx
c_2 = \int K(x)^2\,dx
c_3 = \int (f''(x))^2\,dx.

When the optimal choice of bandwidth is chosen, the risk function is \scriptstyle R(f, \hat f(x))\, \approx\, \tfrac{c_4}{n^{4/5}} for some constant c4 > 0. It can be shown that, under weak assumptions, there cannot exist a non-parametric estimator that converges at a faster rate than the kernel estimator. Note that the n−4/5 rate is slower than the typical n−1 convergence rate of parametric methods.

It is possible to optimize the bandwidth by leave-one-out cross validation.[1]

[edit] Statistical implementation

  • In Matlab, kernel density estimation is implemented through the ksdensity function, but this function does not provide automatic data-driven bandwidth. A free Matlab software which implements an automatic bandwidth selection method is available from the Matlab repository [1] for 1 dimensional data and [2] for 2 dimensional data.
  • An example of implementing kernel density estimation in Mathematica is available here.
  • In Stata, it is implemented through kdensity; for example histogram x, kdensity.
  • In R, it is implemented through the density function (univariate), the kde2d function in the MASS package (bivariate), and the npudens function in the np package (multivariate allowing for numeric and categorical data types with a range of kernel functions and automatic bandwidth selectors).
  • In SAS, proc kde can be used to estimate univariate and bivariate kernel densities.
  • In SciPy, scipy.stats.gaussian_kde can be used to perform gaussian kernel density estimation in arbitrary dimensions, including bandwidth estimation.
  • In Perl, an implementation can be found in the Statistics-KernelEstimation module [3]
  • In Java, the Weka (machine learning) package provides weka.estimators.KernelEstimator[4], among others.
  • In Gnuplot, kernel desity esimation is implemented by the smooth kdensity option, the datafile can contain weigth and bandwidth for each point, or the bandwidth can be set automatically.

[edit] Example of Density Estimation in R programming language

This example is based on the Old Faithful Geyser, a tourist attraction located in Yellowstone National Park. This famous dataset containing 272 records consists of two variables, eruption duration (minutes) and waiting time until the next eruption (minutes). The data is taken from the datasets package of the R programming language.

We consider estimating the joint density of eruption duration and waiting times using the R np package that employs automatic (data-driven) bandwidth selection that is optimal for joint density estimates; see the np vignette for an introduction to the np package. The figure below shows the joint density estimate using a second order Gaussian kernel.

Estimated joint density.

[edit] Script for example

The following commands of the R programming language use the npudens() function to deliver optimal smoothing and to create the figure given above. These commands can be entered at the command prompt by using cut and paste.

library(np)
library(datasets)
data(faithful)

f <- npudens(~eruptions+waiting,data=faithful)

plot(f,view="fixed",neval=100,phi=30,main="",xtrim=-0.2)

[edit] See also

[edit] External links

[edit] References

  1. ^ Finn Årup Nielsen; Lars Kai Hansen (March 2002). "Modeling of activation data in the BrainMapTM: Detection of outliers". Human Brain Mapping 15 (3): 146–156. doi:10.1002/hbm.10012. PMID 11835605. http://www2.imm.dtu.dk/pubdb/views/publication_details.php?id=197. 
  • Li, Q. and Racine, J.S. Nonparametric Econometrics: Theory and Practice. Princeton University Press, 2007, ISBN 0691121613.
  • Parzen E. (1962). On estimation of a probability density function and mode, Ann. Math. Stat. 33, pp. 1065–1076.
  • Duda, R. and Hart, P. (1973). Pattern Classification and Scene Analysis. John Wiley & Sons. ISBN 0-471-22361-1.
  • Wasserman, L. (2005). All of Statistics: A Concise Course in Statistical Inference, Springer Texts in Statistics.
Retrieved from "http://en.wikipedia.org/wiki/Kernel_density_estimation"
Personal tools