Del in cylindrical and spherical coordinates

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This is a list of some vector calculus formulae of general use in working with various coordinate systems.

[edit] Note

  • This page uses standard physics notation. For spherical coordinates, θ is the angle between the z axis and the radius vector connecting the origin to the point in question. φ is the angle between the projection of the radius vector onto the x-y plane and the x axis. Some (American mathematics) sources reverse this definition.
  • The function atan2(y, x) is used instead of the mathematical function arctan(y/x) due to its domain and image. The classical arctan(y/x) has an image of (-π/2, +π/2), whereas atan2(y, x) is defined to have an image of (-π, π]. (The expressions for the Nabla in spherical coordinates may need to be corrected)
Table with the del operator in cylindrical, spherical and parabolic cylindrical coordinates
Operation Cartesian coordinates (x,y,z) Cylindrical coordinates (ρ,φ,z) Spherical coordinates (r,θ,φ) Parabolic cylindrical coordinates (σ,τ,z)
Definition
of
coordinates		 \begin{matrix} \rho & = & \sqrt{x^2+y^2} \\ \phi & = & \arctan(y/x) \\ z & = & z \end{matrix} \begin{matrix} x & = & \rho\cos\phi \\ y & = & \rho\sin\phi \\ z & = & z \end{matrix} \begin{matrix} x & = & r\sin\theta\cos\phi \\ y & = & r\sin\theta\sin\phi \\ z & = & r\cos\theta \end{matrix} \begin{matrix} x & = & \sigma \tau\\ y & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}
\begin{matrix} r & = & \sqrt{x^2+y^2+z^2} \\ \theta & = & \arctan{\left(\frac{\sqrt{x^2+y^2}}{z}\right)}\\ \phi & = & \arctan(y/x) \\ \end{matrix} \begin{matrix} r & = & \sqrt{\rho^2 + z^2} \\ \theta & = & \arctan{(\rho/z)}\\ \phi & = & \phi \end{matrix} \begin{matrix} \rho & = & r\sin(\theta) \\ \phi & = & \phi\\ z & = & r\cos(\theta) \end{matrix} \begin{matrix} \rho\cos\phi & = & \sigma \tau\\ \rho\sin\phi & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}
Definition
of
unit
vectors		 \begin{matrix} \boldsymbol{\hat \rho} & = & \frac{x}{\rho}\mathbf{\hat x}+\frac{y}{\rho}\mathbf{\hat y} \\ \boldsymbol{\hat\phi} & = & -\frac{y}{\rho}\mathbf{\hat x}+\frac{x}{\rho}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix} \begin{matrix} \mathbf{\hat x} & = & \cos\phi\boldsymbol{\hat \rho}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\phi\boldsymbol{\hat \rho}+\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix} \begin{matrix} \mathbf{\hat x} & = & \sin\theta\cos\phi\boldsymbol{\hat r}+\cos\theta\cos\phi\boldsymbol{\hat\theta}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\theta\sin\phi\boldsymbol{\hat r}+\cos\theta\sin\phi\boldsymbol{\hat\theta}+\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta \boldsymbol{\hat r}-\sin\theta \boldsymbol{\hat\theta} \\ \end{matrix} \begin{matrix} \boldsymbol{\hat \sigma} & = & \frac{\tau}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat x}-\frac{\sigma}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat y} \\ \boldsymbol{\hat\tau} & = & \frac{\sigma}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat x}+\frac{\tau}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}
\begin{matrix} \mathbf{\hat r} & = & \frac{x\mathbf{\hat x}+y\mathbf{\hat y}+z\mathbf{\hat z}}{r} \\ \boldsymbol{\hat\theta} & = & \frac{xz\mathbf{\hat x}+yz\mathbf{\hat y}-\rho^2\mathbf{\hat z}}{r \rho} \\ \boldsymbol{\hat\phi} & = & \frac{-y\mathbf{\hat x}+x\mathbf{\hat y}}{\rho} \end{matrix} \begin{matrix} \mathbf{\hat r} & = & \frac{\rho}{r}\boldsymbol{\hat \rho}+\frac{ z}{r}\mathbf{\hat z} \\ \boldsymbol{\hat\theta} & = & \frac{z }{r}\boldsymbol{\hat \rho}-\frac{\rho}{r}\mathbf{\hat z} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \end{matrix} \begin{matrix} \boldsymbol{\hat \rho} & = & \sin\theta\mathbf{\hat r}+\cos\theta\boldsymbol{\hat\theta} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta\mathbf{\hat r}-\sin\theta\boldsymbol{\hat\theta} \\ \end{matrix} \begin{matrix} \end{matrix}
A vector field 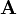\mathbf{A} A_x\mathbf{\hat x} + A_y\mathbf{\hat y} + A_z\mathbf{\hat z} A_\rho\boldsymbol{\hat \rho} + A_\phi\boldsymbol{\hat \phi} + A_z\boldsymbol{\hat z} A_r\boldsymbol{\hat r} + A_\theta\boldsymbol{\hat \theta} + A_\phi\boldsymbol{\hat \phi} A_\sigma\boldsymbol{\hat \sigma} + A_\tau\boldsymbol{\hat \tau} + A_\phi\boldsymbol{\hat z}
Gradient \nabla f {\partial f \over \partial x}\mathbf{\hat x} + {\partial f \over \partial y}\mathbf{\hat y} + {\partial f \over \partial z}\mathbf{\hat z} {\partial f \over \partial \rho}\boldsymbol{\hat \rho} + {1 \over \rho}{\partial f \over \partial \phi}\boldsymbol{\hat \phi} + {\partial f \over \partial z}\boldsymbol{\hat z} {\partial f \over \partial r}\boldsymbol{\hat r} + {1 \over r}{\partial f \over \partial \theta}\boldsymbol{\hat \theta} + {1 \over r\sin\theta}{\partial f \over \partial \phi}\boldsymbol{\hat \phi} \frac{1}{\sqrt{\sigma^{2} + \tau^{2}}} {\partial f \over \partial \sigma}\boldsymbol{\hat \sigma} + \frac{1}{\sqrt{\sigma^{2} + \tau^{2}}} {\partial f \over \partial \tau}\boldsymbol{\hat \tau} + {\partial f \over \partial z}\boldsymbol{\hat z}
Divergence \nabla \cdot \mathbf{A} {\partial A_x \over \partial x} + {\partial A_y \over \partial y} + {\partial A_z \over \partial z} {1 \over \rho}{\partial \left( \rho A_\rho \right) \over \partial \rho} + {1 \over \rho}{\partial A_\phi \over \partial \phi} + {\partial A_z \over \partial z} {1 \over r^2}{\partial \left( r^2 A_r \right) \over \partial r} + {1 \over r\sin\theta}{\partial \over \partial \theta} \left( A_\theta\sin\theta \right) + {1 \over r\sin\theta}{\partial A_\phi \over \partial \phi} \frac{1}{\sigma^{2} + \tau^{2}}{\partial A_\sigma \over \partial \sigma} + \frac{1}{\sigma^{2} + \tau^{2}}{\partial A_\tau \over \partial \tau} + {\partial A_z \over \partial z}


Curl \nabla \times \mathbf{A} \begin{matrix} \displaystyle\left({\partial A_z \over \partial y} - {\partial A_y \over \partial z}\right) \mathbf{\hat x} & + \\ \displaystyle\left({\partial A_x \over \partial z} - {\partial A_z \over \partial x}\right) \mathbf{\hat y} & + \\ \displaystyle\left({\partial A_y \over \partial x} - {\partial A_x \over \partial y}\right) \mathbf{\hat z} & \ \end{matrix} \begin{matrix} \displaystyle\left({1 \over \rho}{\partial A_z \over \partial \phi} - {\partial A_\phi \over \partial z}\right) \boldsymbol{\hat \rho} & + \\ \displaystyle\left({\partial A_\rho \over \partial z} - {\partial A_z \over \partial \rho}\right) \boldsymbol{\hat \phi} & + \\ \displaystyle{1 \over \rho}\left({\partial \left( \rho A_\phi \right) \over \partial \rho} - {\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat z} & \ \end{matrix} \begin{matrix} \displaystyle{1 \over r\sin\theta}\left({\partial \over \partial \theta} \left( A_\phi\sin\theta \right) - {\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat r} & + \\ \displaystyle{1 \over r}\left({1 \over \sin\theta}{\partial A_r \over \partial \phi} - {\partial \over \partial r} \left( r A_\phi \right) \right) \boldsymbol{\hat \theta} & + \\ \displaystyle{1 \over r}\left({\partial \over \partial r} \left( r A_\theta \right) - {\partial A_r \over \partial \theta}\right) \boldsymbol{\hat \phi} & \ \end{matrix} \begin{matrix} \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}{\partial A_z \over \partial \tau} - {\partial A_\tau \over \partial z}\right) \boldsymbol{\hat \sigma} & - \\ \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}{\partial A_z \over \partial \sigma}- {\partial A_\sigma \over \partial z}\right) \boldsymbol{\hat \tau} & + \\ \displaystyle\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}\left({\partial \left( \rho A_\phi \right) \over \partial \rho} - {\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat z} & \ \end{matrix}
Laplace operator 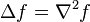\Delta f = \nabla^2 f {\partial^2 f \over \partial x^2} + {\partial^2 f \over \partial y^2} + {\partial^2 f \over \partial z^2} {1 \over \rho}{\partial \over \partial \rho}\left(\rho {\partial f \over \partial \rho}\right) + {1 \over \rho^2}{\partial^2 f \over \partial \phi^2} + {\partial^2 f \over \partial z^2} {1 \over r^2}{\partial \over \partial r}\!\left(r^2 {\partial f \over \partial r}\right) \!+\!{1 \over r^2\!\sin\theta}{\partial \over \partial \theta}\!\left(\sin\theta {\partial f \over \partial \theta}\right) \!+\!{1 \over r^2\!\sin^2\theta}{\partial^2 f \over \partial \phi^2} \frac{1}{\sigma^{2} + \tau^{2}} \left( \frac{\partial^{2} f}{\partial \sigma^{2}} + \frac{\partial^{2} f}{\partial \tau^{2}} \right) + \frac{\partial^{2} f}{\partial z^{2}}
Vector Laplacian \Delta \mathbf{A} = \nabla^2 \mathbf{A} \Delta A_x \mathbf{\hat x} + \Delta A_y \mathbf{\hat y} + \Delta A_z \mathbf{\hat z} \begin{matrix} \displaystyle\left(\Delta A_\rho - {A_\rho \over \rho^2} - {2 \over \rho^2}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat \rho} & + \\ \displaystyle\left(\Delta A_\phi - {A_\phi \over \rho^2} + {2 \over \rho^2}{\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat\phi} & + \\ \displaystyle\left(\Delta A_z \right) \boldsymbol{\hat z} & \ \end{matrix} \begin{matrix} \left(\Delta A_r - {2 A_r \over r^2} - {2 \over r^2\sin\theta}{\partial \left(A_\theta \sin\theta\right) \over \partial\theta} - {2 \over r^2\sin\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat r} & + \\ \left(\Delta A_\theta - {A_\theta \over r^2\sin^2\theta} + {2 \over r^2}{\partial A_r \over \partial \theta} - {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat\theta} & + \\ \left(\Delta A_\phi - {A_\phi \over r^2\sin^2\theta} + {2 \over r^2\sin\theta}{\partial A_r \over \partial \phi} + {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat\phi} & \end{matrix}
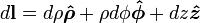Differential displacement d\mathbf{l} = dx\mathbf{\hat x} + dy\mathbf{\hat y} + dz\mathbf{\hat z} d\mathbf{l} = d\rho\boldsymbol{\hat \rho} + \rho d\phi\boldsymbol{\hat \phi} + dz\boldsymbol{\hat z} d\mathbf{l} = dr\mathbf{\hat r} + rd\theta\boldsymbol{\hat \theta} + r\sin\theta d\phi\boldsymbol{\hat \phi} d\mathbf{l} = \sqrt{\sigma^{2} + \tau^{2}} d\sigma\boldsymbol{\hat \sigma} + \sqrt{\sigma^{2} + \tau^{2}} d\tau\boldsymbol{\hat \tau} + dz\boldsymbol{\hat z}
Differential normal area \begin{matrix}d\mathbf{S} = &dy\,dz\,\mathbf{\hat x} + \\ &dx\,dz\,\mathbf{\hat y} + \\ &dx\,dy\,\mathbf{\hat z}\end{matrix} \begin{matrix} d\mathbf{S} = & \rho\, d\phi\, dz\,\boldsymbol{\hat \rho} + \\ & d\rho \,dz\,\boldsymbol{\hat \phi} + \\ & \rho \,d\rho d\phi \,\mathbf{\hat z} \end{matrix} \begin{matrix} d\mathbf{S} = & r^2 \sin\theta \,d\theta \,d\phi \,\mathbf{\hat r} + \\ & r\sin\theta \,dr\,d\phi \,\boldsymbol{\hat \theta} + \\ & r\,dr\,d\theta\,\boldsymbol{\hat \phi} \end{matrix} \begin{matrix} d\mathbf{S} = & \sqrt{\sigma^{2} + \tau^{2}}, d\tau\, dz\,\boldsymbol{\hat \sigma} + \\ & \sqrt{\sigma^{2} + \tau^{2}} d\sigma\,dz\,\boldsymbol{\hat \tau} + \\ & \sigma^{2} + \tau^{2} d\sigma, d\tau \,\mathbf{\hat z} \end{matrix}
Differential volume dV = dx\,dy\,dz \, dV = \rho\, d\rho\, d\phi\, dz\, dV = r^2\sin\theta \,dr\,d\theta\, d\phi\, dV = \left( \sigma^{2} + \tau^{2} \right) d\sigma d\tau dz,
Non-trivial calculation rules:
  1. \operatorname{div\ grad\ } f = \nabla \cdot (\nabla f) = \nabla^2 f = \Delta f (Laplacian)
  2. \operatorname{curl\ grad\ } f = \nabla \times (\nabla f) = \mathbf{0}
  3. \operatorname{div\ curl\ } \mathbf{A} = \nabla \cdot (\nabla \times \mathbf{A}) = 0
  4. \operatorname{curl\ curl\ } \mathbf{A} = \nabla \times (\nabla \times \mathbf{A}) = \nabla (\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A} (using Lagrange's formula for the cross product)
  5. \Delta f g = f \Delta g + 2 \nabla f \cdot \nabla g + g \Delta f

[edit] See also

Retrieved from "http://en.wikipedia.org/wiki/Del_in_cylindrical_and_spherical_coordinates"
Personal tools