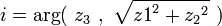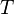Orbital elements

From Wikipedia, the free encyclopedia

In celestial mechanics, the elements of an orbit are the parameters needed to specify that orbit uniquely. Orbital elements are generally considered in classical two-body systems, where a Kepler orbit is used (derived from Newton's laws of motion and Newton's law of universal gravitation). There are many different ways to mathematically describe the same orbit, but certain schemes each consisting of a set of six parameters are commonly used in astronomy and orbital mechanics.

A real orbit (and its elements) changes over time due to gravitational perturbations by other objects and the effects of relativity. A Keplerian orbit is merely a mathematical approximation at a particular time.

[edit] Number of parameters needed

Given an inertial frame of reference and an arbitrary epoch (a specified point in time), exactly six parameters are necessary to unambiguously define an arbitrary and unperturbed orbit.

This is because the problem contains six degrees of freedom. These correspond to the three spatial dimensions which define position (the x, y, z in a Cartesian coordinate system), plus the velocity in each of these dimensions. These can be described as orbital state vectors, but this is often an inconvenient way to represent an orbit, which is why Keplerian elements (described below) are commonly used instead.

Sometimes the epoch is considered a "seventh" orbital parameter, rather than part of the reference frame.

If the epoch is defined to be at the moment when one of the elements is zero, the number of unspecified elements is reduced to five. (The sixth parameter is still necessary to define the orbit; it is merely numerically set to zero by convention or "moved" into the definition of the epoch with respect to real-world clock time.)

[edit] Keplerian elements

In this diagram, the orbital plane (yellow) intersects a reference plane (gray). For earth-orbiting satellites, the reference plane is usually the earth's equatorial plane, and for satellites in solar orbits it is the ecliptic plane. The intersection is called the line of nodes, as it connects the center of mass with the ascending and descending nodes. This plane, together with the Vernal Point, (♈) establishes a reference frame.

The traditional orbital elements are the six Keplerian elements, after Johannes Kepler and his laws of planetary motion.

Two elements define the shape and size of the ellipse:

Eccentricity ( $e\,\!$ ) - shape of the ellipse, describing how flattened it is compared with a circle. (not marked in diagram)
Semimajor axis ( $a\,\!$ ) - similar to the radius of a circle, its length is the distance between the geometric center of the orbital ellipse with the periapsis (point of closest approach to the central body), passing through the focal point where the center of mass resides.

Two define the orientation of the orbital plane in which the ellipse is embedded:

Inclination - vertical tilt of the ellipse with respect to the reference plane, measured at the ascending node (where the orbit passes upward through the reference plane). (green angle 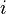$i\,\!$ in diagram)
Longitude of the ascending node - horizontally orients the ascending node of the ellipse (where the orbit passes upward through the reference plane) with respect to the reference frame's vernal point. (green angle 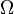$\Omega\,\!$ in diagram)

And finally:

Argument of periapsis defines the orientation of the ellipse (in which direction it is flattened compared to a circle) in the orbital plane, as an angle measured from the ascending node to the semimajor axis. (violet angle $\omega\,\!$ in diagram)
Mean anomaly at epoch ( $M_o\,\!$ ) defines the position of the orbiting body along the ellipse at a specific time (the "epoch").

The mean anomaly is a mathematically convenient "angle" which varies linearly with time, but which does not correspond to a real geometric angle. It can be converted into the true anomaly $\nu\,\!$ , which does represent the real geometric angle in the plane of the ellipse, between periapsis (closest approach to the central body) and the position of the orbiting object at any given time. Thus, the true anomaly is shown as the red angle $\nu\,\!$ in the diagram, and the mean anomaly is not shown.

The angles of inclination, longitude of the ascending node, and argument of periapsis can also be described as the Euler angles defining the orientation of the orbit relative to the reference coordinate system.

Note that non-elliptical orbits also exist; an orbit is a parabola if it has an eccentricity of 1, and it is a hyperbola if it has an eccentricity greater than 1.

[edit] Alternative parametrizations

Keplerian elements can be obtained from orbital state vectors (x-y-z coordinates for position and velocity) by manual transformations or with computer software.^[1]

Other orbital parameters can be computed from the Keplerian elements such as the period, apoapsis and periapsis. (When orbiting the earth, the last two terms are known as the apogee and perigee.) It is common to specify the period instead of the semi-major axis in Keplerian element sets, as each can be computed from the other provided the standard gravitational parameter, GM, is given for the central body.

Instead of the the mean anomaly at epoch, the mean anomaly 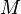$M\,\!$ , mean longitude, true anomaly $\nu_o\,\!$ , or (rarely) the eccentric anomaly might be used.

Using, for example, the "mean anomaly" instead of "mean anomaly at epoch" means that time $t$ must be specified as a "seventh" orbital element. Sometimes it is assumed that mean anomaly is zero at the epoch (by choosing the appropriate definition of the epoch), leaving only the five other orbital elements to be specified.

[edit] Euler angle transformations

The angles $Ω, i,ω$ are the Euler angles ( $α,β,γ$ with the notations of that article) characterizing the orientation of the coordinate system

$\hat{x},\hat{y},\hat{z}$

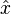with $\hat{x},\hat{y}$ in the orbital plane and with $\hat{x}$ in the direction to the pericenter.

The transformation from the euler angles $Ω, i,ω$ to $\hat{x},\hat{y},\hat{z}$ is:

$x_1= \cos \Omega \cdot \cos \omega - \ sin \Omega \cdot \cos i \cdot \sin \omega$

$x_2= \sin \Omega \cdot \cos \omega + \cos \Omega \cdot \cos i \cdot \sin \omega$

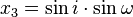
$x_3= \sin i \cdot \sin \omega$

$y_1=-\cos \Omega \cdot \sin \omega - \sin \Omega \cdot \cos i \cdot \cos \omega$

$y_2=-\sin \Omega \cdot \sin \omega + \cos \Omega \cdot \cos i \cdot \cos \omega$

$y_3= \sin i \cdot \cos \omega$

$z_1= \sin i \cdot \sin \Omega$

$z_2=-\sin i \cdot \cos \Omega$

z 3 = cos i

The transformation from $\hat{x},\hat{y},\hat{z}$ to Euler angles $Ω, i,ω$ is:

$\Omega= \operatorname{arg}(\ -z_2\ ,\ z_1\ )$

$i = \operatorname{arg}(\ z_3\ ,\ \sqrt{{z 1}^2 + {z_2}^2}\ )$

$\omega= \operatorname{arg}(\ y_3\ ,\ x_3\ )$

where $\operatorname{arg}(x\ ,\ y)$ signifies the polar argument that can be computed with the standard function ATAN2(y,x) (or in double precision DATAN2(y,x)) available in for example the programming language FORTRAN.

[edit] Perturbations and elemental variance

Unperturbed, two-body orbits are always conic sections, so the Keplerian elements define an ellipse, parabola, or hyperbola. Real orbits have perturbations, so a given set of Keplerian elements accurately describes an orbit only at the epoch. Evolution of the orbital elements takes place due to the gravitational pull of bodies other than the primary, the nonsphericity of the primary, atmospheric drag, relativistic effects, radiation pressure, electromagnetic forces, and so on.

Keplerian elements can often be used to produce useful predictions at times near the epoch. Alternatively, real trajectories can be modeled as a sequence of Keplerian orbits that osculate ("kiss" or touch) the real trajectory. They can also be described by the so-called planetary equations, differential equations which come in different forms developed by Lagrange, Gauss, Delaunay, Poincaré, or Hill.

[edit] Two-line elements

Main article: Two-line elements

Keplerian elements parameters can be encoded as text in a number of formats. The most common of them is the NASA/NORAD "two-line elements"(TLE) format[1] , originally designed for use with 80-column punched cards, but still in use because it is the most common format, and works as well as any other.
Depending on the application and object orbit, the data derived from TLEs older than 30 days can become unreliable. Orbital positions can be calculated from TLEs through the SGP/SGP4/SDP4/SGP8/SDP8 algorithms.^[2]

Line 1
Column Characters Description
-----  ---------- -----------
 1        1       Line No. Identification
 3        5       Catalog No.
 8        1       Security Classification
10        8       International Identification
19       14       YRDOY.FODddddd
34        1       Sign of first time derivative
35        9       1st Time Derivative
45        1       Sign of 2nd Time Derivative
46        5       2nd Time Derivative
51        1       Sign of 2nd Time Derivative Exponent
52        1       Exponent of 2nd Time Derivative
54        1       Sign of Bstar/Drag Term
55        5       Bstar/Drag Term
60        1       Sign of Exponent of Bstar/Drag Term
61        1       Exponent of Bstar/Drag Term
63        1       Ephemeris Type
65        4       Element Number
69        1       Check Sum, Modulo 10

Line 2
Column Characters Description
-----  ---------- -----------
 1       1        Line No. Identification
 3       5        Catalog No.
 9       8        Inclination
18       8        Right Ascension of Ascending Node
27       7        Eccentricity with assumed leading decimal
35       8        Argument of the Perigee
44       8        Mean Anomaly
53      11        Revolutions per Day (Mean Motion)
64       5        Revolution Number at Epoch
69       1        Check Sum Modulo 10

Example of a two line element:^[3]

1 27651U 03004A   07083.49636287  .00000119  00000-0  30706-4 0  2692
2 27651 039.9951 132.2059 0025931 073.4582 286.9047 14.81909376225249

[edit] See also

[edit] References

^ For example, with VEC2TLE
^ Explanatory Supplement to the Astronomical Almanac. 1992. K. P. Seidelmann, Ed., University Science Books, Mill Valley, California.
^ SORCE - Orbit Data