Cyclomatic complexity

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Cyclomatic complexity (or conditional complexity) is a software metric (measurement). It was developed by Thomas J. McCabe Sr. in 1976 and is used to measure the complexity of a program. It directly measures the number of linearly independent paths through a program's source code.

The concept, although not the method, is somewhat similar to that of general text complexity measured by the Flesch-Kincaid Readability Test.

Cyclomatic complexity is computed using the control flow graph of the program: the nodes of the graph correspond to indivisible groups of commands of a program, and a directed edge connects two nodes if the second command might be executed immediately after the first command.

Cyclomatic complexity may also be applied to individual functions, modules, methods or classes within a program.

Contents

[edit] Description

The cyclomatic complexity of a section of source code is the count of the number of linearly independent paths through the source code. For instance, if the source code contained no decision points such as IF statements or FOR loops, the complexity would be 1, since there is only a single path through the code. If the code had a single IF statement containing a single condition there would be two paths through the code, one path where the IF statement is evaluated as TRUE and one path where the IF statement is evaluated as FALSE.

Mathematically, the cyclomatic complexity of a structured program[1] is defined with reference to a directed graph containing the basic blocks of the program, with an edge between two basic blocks if control may pass from the first to the second (the control flow graph of the program). The complexity is then defined as:[2]

M = E − N + 2P

where

M = cyclomatic complexity
E = the number of edges of the graph
N = the number of nodes of the graph
P = the number of connected components.

An alternative formulation is to use a graph in which each exit point is connected back to the entry point. In this case, the graph is said to be strongly connected, and the cyclomatic complexity of the program is equal to the cyclomatic number of its graph (also known as the first Betti number), which is defined as:[2]

M = E − N + P

This may be seen as calculating the number of linearly independent cycles that exist in the graph, i.e. those cycles that do not contain other cycles within themselves. Note that because each exit point loops back to the entry point, there is at least one such cycle for each exit point.

For a single program (or subroutine or method), P is always equal to 1. Cyclomatic complexity may, however, be applied to several such programs or subprograms at the same time (e.g., to all of the methods in a class), and in these cases P will be equal to the number of programs in question, as each subprogram will appear as a disconnected subset of the graph.

It can be shown that the cyclomatic complexity of any structured program with only one entrance point and one exit point is equal to the number of decision points (i.e., 'if' statements or conditional loops) contained in that program plus one.[2][3]

Cyclomatic complexity may be extended to a program with multiple exit points; in this case it is equal to:

π - s + 2

where π is the number of decision points in the program, and s is the number of exit points.[3][4]

[edit] Formal definition

 This section does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (March 2009)

Formally, cyclomatic complexity can be defined as a relative Betti number, the size of a relative homology group:

M := b_1(G,t) := \operatorname{rank}\,H_1(G,t)

which is read as “the first homology of the graph G, relative to the terminal nodes t”. This is a technical way of saying “the number of linearly independent paths through the flow graph from an entry to an exit”, where:

  • “linearly independent” corresponds to homology, and means one does not double-count backtracking;
  • “paths” corresponds to first homology: a path is a 1-dimensional object;
  • “relative” means the path must begin and end at an entry or exit point.

This corresponds to the intuitive notion of cyclomatic complexity, and can be calculated as above.

Alternatively, one can compute this via absolute Betti number (absolute homology – not relative) by identifying (gluing together) all terminal nodes on a given component (or equivalently, draw paths connecting the exits to the entrance), in which case (calling the new, augmented graph \tilde G, which is ), one obtains:

M = b_1(\tilde G) = \operatorname{rank}\,H_1(\tilde G)

This corresponds to the characterization of cyclomatic complexity as “number of loops plus number of components”.

[edit] Etymology / Naming

The name Cyclomatic Complexity may at first seem confusing, as this metric does not only count cycles (loops) in the program. It is motivated by the number of different cycles in the program control flow graph, after having added an imagined branch back from the exit node to the entry node.[2]

[edit] Applications

[edit] Limiting complexity during development

One of McCabe's original applications was to limit the complexity of routines during program development; he recommended that programmers should count the complexity of the modules they are developing, and split them into smaller modules whenever the cyclomatic complexity of the module exceeded 10.[2] This practice was adopted by the NIST Structured Testing methodology, with an observation that since McCabe's original publication, the figure of 10 had received substantial corroborating evidence, but that in some circumstances it may be appropriate to relax the restriction and permit modules with a complexity as high as 15. As the methodology acknowledged that there were occasional reasons for going beyond the agreed-upon limit, it phrased its recommendation as: "For each module, either limit cyclomatic complexity to [the agreed-upon limit] or provide a written explanation of why the limit was exceeded."[5]

[edit] Implications for Software Testing

Another application of cyclomatic complexity is in determining the number of test cases that are necessary to achieve thorough test coverage of a particular module.

It is useful because of two properties of the cyclomatic complexity, M, for a specific module:

  • M is an upper bound for the number of test cases that are necessary to achieve a complete branch coverage.
  • M is a lower bound for the number of paths through the control flow graph (CFG). Assuming each test case takes one path, the number of cases needed to achieve path coverage is equal to the number of paths that can actually be taken. But some paths may be impossible, so although the number of paths through the CFG is clearly an upper bound on the number of test cases needed for path coverage, this latter number (of possible paths) is sometimes less than M.

All three of the above numbers may be equal: branch coverage 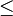\leq cyclomatic complexity 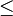\leq number of paths.

For example, consider a program that consists of two sequential if-then-else statements.

if( c1 )
   f1();
else
   f2();
 
if( c2 )
   f3();
else
   f4();

In this exampe, two test cases are sufficient to achieve a complete branch coverage, while four are necessary for complete path coverage. The cyclomatic complexity of the program is 3 (as the strongly-connected graph for the program contains 9 edges, 7 nodes and 1 connected component).

In general, in order to fully test a module all execution paths through the module should be exercised. This implies a module with a high complexity number requires more testing effort than a module with a lower value since the higher complexity number indicates more pathways through the code. This also implies that a module with higher complexity is more difficult for a programmer to understand since the programmer must understand the different pathways and the results of those pathways.

Unfortunately, it is not always practical to test all possible paths through a program. Considering the example above, each time an additional if-then-else statement is added, the number of possible paths doubles. As the program grew in this fashion, it would quickly reach the point where testing all of the paths was impractical.

One common testing strategy, espoused for example by the NIST Structured Testing methodology, is to use the cyclomatic complexity of a module to determine the number of white-box tests that are required to obtain sufficient coverage of the module. In almost all cases, according to such a methodology, a module should have at least as many tests as its cyclomatic complexity; in most cases, this number of tests is adequate to exercise all the relevant paths of the function.[5]

[edit] Cohesion

One would also expect that a module with higher complexity would tend to have lower cohesion (less than functional cohesion) than a module with lower complexity. The possible correlation between higher complexity measure with a lower level of cohesion is predicated on a module with more decision points generally implementing more than a single well defined function. A 2005 study showed stronger correlations between complexity metrics and an expert assessment of cohesion in the classes studied than the correlation between the expert's assessment and metrics designed to calculate cohesion.[6]

However there are certain types of modules that one would expect to have a high complexity number, such as user interface (UI) modules containing source code for data validation and error recovery.[citation needed]

[edit] Correlation to number of defects

A number of studies have investigated cyclomatic complexity's correlation to the number of defects contained in a module. Most such studies find a strong positive correlation between cyclomatic complexity and defects: modules that have the highest complexity tend to also contain the most defects. For example, a 2008 study by metric-monitoring software supplier Enerjy analyzed classes of open-source Java applications and divided them into two sets based on how commonly faults were found in them. They found strong correlation between cyclomatic complexity and their faultiness, with classes with a combined complexity of 11 having a probability of being fault-prone of just 0.28, rising to 0.98 for classes with a complexity of 74.[7]

However, studies that control for program size (i.e., comparing modules that have different complexities but similar size, typically measured in lines of code) are generally less conclusive, with many finding no significant correlation, while others do find correlation. Some researchers who have studied the area question the validity of the methods used by the studies finding no correlation.[8]

Les Hatton claimed recently (Key note at TAIC-PART 2008, Windsor, UK, Sept 2008) that McCabe Cyclomatic Complexity has the same prediction ability as lines of code.[citation needed]

[edit] Notes

  1. ^ Here "structured" means in particular "with a single exit (return statement) per function".
  2. ^ a b c d e McCabe (December 1976). "A Complexity Measure". IEEE Transactions on Software Engineering: 308-320. http://classes.cecs.ucf.edu/eel6883/berrios/notes/Paper%204%20(Complexity%20Measure).pdf. 
  3. ^ a b Belzer, Kent, Holzman and Williams (1992). Encyclopedia of Computer Science and Technology. CRC Press. pp. 367-368. 
  4. ^ Harrison (October 1984). "Applying Mccabe's complexity measure to multiple-exit programs". Software: Practice and Experience (J Wiley & Sons). 
  5. ^ a b McCabe, Watson (1996). "Structured Testing: A Testing Methodology Using the Cyclomatic Complexity Metric". http://hissa.nist.gov/HHRFdata/Artifacts/ITLdoc/235/title.htm. 
  6. ^ Stein et al (2005). "Exploring the relationship between cohesion and complexity". Journal of Computer Science 1 (2): 137-144. 
  7. ^ Rich Sharpe. "McCabe Cyclomatic Complexity: the proof in the pudding". Enerjy. http://www.enerjy.com/blog/?p=198. 
  8. ^ Kan (2003). Metrics and Models in Software Quality Engineering. Addison-Wesley. pp. 316-317. ISBN 0201729156. 

[edit] See also

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Cyclomatic_complexity"
Personal tools