Googol
From Wikipedia, the free encyclopedia
A googol is the large number 10100, that is, the digit 1 followed by one hundred zeros (in decimal representation). The term was coined in 1938[1] by Milton Sirotta (1929–1980), nephew of American mathematician Edward Kasner. Kasner popularized the concept in his book Mathematics and the Imagination (1940).
Googol is of the same order of magnitude as the factorial of 70 (70! being approximately 1.198 googol, or 10 to the power 100.0784), and its only prime factors are 2 and 5 (100 of each). In binary it would take up 333 bits. A googol has no particular significance in mathematics, but is useful when comparing with other very large quantities such as the number of subatomic particles in the visible universe or the number of possible chess games. Edward Kasner created it to illustrate the difference between an unimaginably large number and infinity, and in this role it is sometimes used in teaching mathematics.
A googol can be written in conventional notation as follows:
- 1 googol
- = 10100
- = 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
Its official English number name is ten duotrigintillion on the short scale, ten thousand sexdecillion on the long scale, or ten sexdecilliard on the Peletier long scale.
Contents |
[edit] Googolplex
A googolplex is the number one followed by one googol zeroes, or ten raised to the power of one googol:
- 10googol = 10(10100).
In the documentary Cosmos, physicist and broadcast personality Carl Sagan estimated that writing a googolplex in base-10 numerals (i.e., "10,000,000,000...") would be physically impossible, since doing so would require more space than the known universe occupies.
[edit] Googol and comparable large numbers
A googol is greater than the number of atoms in the observable universe, which has been variously estimated from 1079 up to 1081[2][3].
Less than a googol Planck times have elapsed since the Big Bang (the current figure stands at around 8×1060 Planck times). Similarly, the size of the observable universe is about 9×10185 cubic Planck lengths.
From the previous figures it can be seen that a list of positions of every particle at every possible instant of time, at the maximum possible accuracy, would contain well over a googol entries (of the order of 10325), but still far less than a googolplex.
Avogadro's number, 6.02214179 × 1023, is exactly the number of 12C atoms in 12 grams (0.012 kg) of unbound 12C in its ground state. It is perhaps the most widely known large number from chemistry and physics. Avogadro's number is less than the fourth root of a googol.
Black holes are presumed to evaporate because they faintly give off Hawking radiation; if so, a supermassive black hole would take about a googol years to evaporate.[4]
A googol is roughly equal to the factorial of 70; this number is 1.1987... × 10100. It follows that there are more than a googol ways to arrange 70 objects into a sequence.
The Shannon number, 10120, a rough lower bound on the number of possible chess games, is more than a googol.
A googol is considerably less than the number described in the ancient Archimedes' story of The Sand Reckoner, namely
But it should be noted that the system invented by Archimedes is reminiscent of a positional numeral system with base 108, so that Archimedes' number could be written
that is, one googol in base 108.
[edit] In popular culture
- Googol was the answer to the million-pound question: "A number one followed by 100 zeros is known by what name?" on Who Wants to Be a Millionaire? when Major Charles Ingram attempted to defraud the quiz show on 10 September 2001. The other options were a megatron, a gigabit or a nanomole.[5]
- Googol is one of the 336 vocabulary words in the board game Balderdash, and their definition on the back of the card is "The number one followed by 100 zeros."
- In the January 23, 1963 Peanuts strip, Lucy asks Schroeder what the chances are of them getting married, and Schroeder responds "Oh, I'd say about 'googol' to one."
- In an episode of the animated series Teenage Mutant Ninja Turtles: Fast Forward, the "Gaminator" video games system is said to have a "3-googolhertz processor."
- "A googolplex is precisely as far from infinity as is the number one." — Carl Sagan, Cosmos
- The company name Google is a misspelling of the word "Googol" made by founders Larry Page and Sergey Brin, as described in the book The Google Story by David A. Vise.
- Was a question in the 1995 film, The Computer Wore Tennis Shoes, when the two colleges were answering against each other. "What is a googol?" was the question. Norwood Gills answered with "One, followed by a hundred zeros".
- In Back to the Future III, Emmett Brown states that Clara was "One in a googolplex"
- In Steve Martin's comedy album Comedy Is Not Pretty!, Martin talks about buying a googolphonic stereo system (which he erroneously describes as having, "the highest number of speakers before infinity...") after not being satisfied with his stereophonic, quadraphonic, then dodecaphonic systems.
[edit] See also
[edit] References
- ^ Kasner, Edward and James Newman, Mathematics and the Imagination, 1940, Simon and Schuster, New York. ISBN 0-486-41703-4
- ^ Estimate of the number of atoms in the Universe; 1078 up to 1081
- ^ Another estimate of the number of atoms in the Universe; 4 × 1079
- ^ On the dark side, p.4
- ^ Millionaire's route to the top prize
|
|||||||||||||||||||
[edit] External links
- "Googolgono" History of Google and Googol.
- Eric W. Weisstein, Googol at MathWorld.
- googol at PlanetMath.
- "Tridecabillion" by Paul Niquette
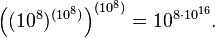
![\left[\left((10)^{(10)}\right)^{10}\right]_{10^8}=\left[10^{100}\right]_{10^8},](http://upload.wikimedia.org/math/5/9/b/59bf3ad009f6e4fe002dacf16c554e06.png)

