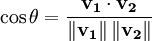Vector space model

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Vector space model (or term vector model) is an algebraic model for representing text documents (and any objects, in general) as vectors of identifiers, such as, for example, index terms. It is used in information filtering, information retrieval, indexing and relevancy rankings. Its first use was in the SMART Information Retrieval System.

Contents

[edit] Definitions

A document is represented as a vector. Each dimension corresponds to a separate term. If a term occurs in the document, its value in the vector is non-zero. Several different ways of computing these values, also known as (term) weights, have been developed. One of the best known schemes is tf-idf weighting (see the example below).

The definition of term depends on the application. Typically terms are single words, keywords, or longer phrases. If the words are chosen to be the terms, the dimensionality of the vector is the number of words in the vocabulary (the number of distinct words occurring in the corpus).

[edit] Applications

Relevancy rankings of documents in a keyword search can be calculated, using the assumptions of document similarities theory, by comparing the deviation of angles between each document vector and the original query vector where the query is represented as same kind of vector as the documents.

In practice, it is easier to calculate the cosine of the angle between the vectors instead of the angle:

\cos{\theta} = \frac{\mathbf{v_1} \cdot \mathbf{v_2}}{\left\| \mathbf{v_1} \right\| \left \| \mathbf{v_2} \right\|}

A cosine value of zero means that the query and document vector were orthogonal and had no match (i.e. the query term did not exist in the document being considered). See cosine similarity for further information.

[edit] Example: tf-idf weights

In the classic vector space model proposed by Salton, Wong and Yang [1] the term specific weights in the document vectors are products of local and global parameters. The model is known as term frequency-inverse document frequency model. The weight vector for document d is \mathbf{v}_d = [w_{1,d}, w_{2,d}, \ldots, w_{N,d}]^T, where

w_{t,d} = \mathrm{tf}_t \cdot \log{\frac{|D|}{|\{t \in d\}|}}

and

  • tft is term frequency of term t in document d (a local parameter)
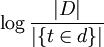  • \log{\frac{|D|}{|\{t \in d\}|}} is inverse document frequency (a global parameter). | D | is the total number of documents in the document set; 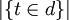|\{t \in d\}| is the number of documents containing the term t.

In a simpler Term Count Model the term specific weights do not include the global parameter. Instead the weights are just the counts of term occurrences: wt,d = tft.

[edit] Limitations

The vector space model has the following limitations:

  1. Long documents are poorly represented because they have poor similarity values (a small scalar product and a large dimensionality)
  2. Search keywords must precisely match document terms; word substrings might result in a "false positive match"
  3. Semantic sensitivity; documents with similar context but different term vocabulary won't be associated, resulting in a "false negative match".
  4. The order in which the terms appear in the document is lost in the vector space representation.

[edit] Models based on and extending the vector space model

Models based on and extending the vector space model include:

  • Generalized vector space model
  • (enhanced) Topic-based Vector Space Model [1] (eTVSM) — Extends the vector space model by removing the constraint that the term-vectors be orthogonal. In contrast to the generalized vector space model the (enhanced) Topic-based Vector Space Model does not depend on concurrence-based similarities between terms. The enhancement of the enhanced Topic-based Vector Space Model (compared to the not enhanced one) is a proposal on how to derive term-vectors from an Ontology.
  • Latent semantic analysis
  • DSIR model
  • Term Discrimination

[edit] Further reading

[edit] See also

[edit] References

  1. ^ G. Salton , A. Wong , C. S. Yang, A vector space model for automatic indexing, Communications of the ACM, v.18 n.11, p.613-620, Nov. 1975
Retrieved from "http://en.wikipedia.org/wiki/Vector_space_model"
Personal tools