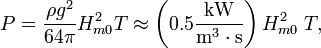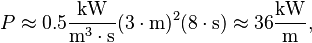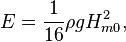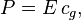Wave power
From Wikipedia, the free encyclopedia
| Renewable energy |
|---|
| Biofuel Biomass Geothermal Hydro power Solar power Tidal power Wave power Wind power |
Wave power is the transport of energy by ocean surface waves, and the capture of that energy to do useful work — for example for electricity generation, water desalination, or the pumping of water (into reservoirs). Wave power is a renewable energy source.
Though often co-mingled, wave power is distinct from the diurnal flux of tidal power and the steady gyre of ocean currents. Wave power generation is not currently a widely employed commercial technology although there have been attempts at using it since at least 1890.[1] The world's first commercial wave farm is based in Portugal,[2] at the Aguçadora Wave Park, which consists of three 750 kilowatt Pelamis devices.[3]
Contents |
[edit] Physical concepts

A = At deep water. The orbital motion of fluid particles decreases rapidly with increasing depth below the surface.
B = At shallow water (ocean floor is now at B). The elliptical movement of a fluid particle flattens with decreasing depth.
1 = Propagation direction.
2 = Wave crest.
3 = Wave trough.
Waves are generated by wind passing over the sea: as long as the waves propagate slower than the wind speed just above the waves, there is an energy transfer from the wind to the most energetic waves. Both air pressure differences between the upwind and the lee side of a wave crest, as well as friction on the water surface by the wind shear stress causes the growth of the waves.[4] The wave height increases with increases in (see Ocean surface wave):
- wind speed,
- time duration of the wind blowing,
- fetch — the distance of open water that the wind has blown over, and
- water depth (in case of shallow water effects, for water depths less than half the wavelength).[5]
In general, large waves are more powerful. Specifically, wave power is determined by wave height, wave speed, wavelength, and water density.
Wave size is determined by wind speed and fetch (the distance over which the wind excites the waves) and by the depth and topography of the seafloor (which can focus or disperse the energy of the waves). A given wind speed has a matching practical limit over which time or distance will not produce larger waves. This limit is called a "fully developed sea."
Oscillatory motion is highest at the surface and diminishes exponentially with depth. However, for standing waves (clapotis) near a reflecting coast, wave energy is also present as pressure oscillations at great depth, producing microseisms.[4] These pressure fluctuations at greater depth are too small to be interesting from the point of view of wave power.
The waves propagate on the ocean surface, and the wave energy is also transported horizontally with the group velocity. The mean transport rate of the wave energy through a vertical plane of unit width, parallel to a wave crest, is called the wave energy flux (or wave power, which must not be confused with the actual power generated by a wave power device).
[edit] Wave power formula
In deep water, if the water depth is larger than half the wavelength, the wave energy flux is
where
- P the wave energy flux per unit wave crest length (kW/m);
- Hm0 is the significant wave height (meter), as measured by wave buoys and predicted by wave forecast models. By definition,[6] Hm0 is four times the standard deviation of the water surface elevation;
- T is the wave period (second);
- ρ is the mass density of the water (kg/m3), and
- g is the acceleration by gravity (m/s2).
The above formula states that wave power is proportional to the wave period and to the square of the wave height. When the significant wave height is given in meters, and the wave period in seconds, the result is the wave power in kilowatts (kW) per meter wavefront length.[7][8]
Example: Consider moderate ocean swells, in deep water, a few kilometers off a coastline, with a wave height of 3 meters and a wave period of 8 seconds. Using the formula to solve for power, we get
meaning there are 36 kilowatts of power potential per meter of coastline.
In major storms, the largest waves offshore are about 15 meters high and have a period of about 15 seconds. According to the above formula, such waves carry about 1.7 MW/m of power across each meter of wavefront.
An effective wave power device captures as much as possible of the wave energy flux. As a result the waves will be of lower height in the region behind the wave power device.
[edit] Wave energy and wave energy flux
In a sea state, the average energy density per unit area of gravity waves on the water surface is proportional to the wave height squared, according to linear wave theory:[4][6]
where E is the mean wave energy density per unit horizontal area (J/m2), the sum of kinetic and potential energy density per unit horizontal area. The potential energy density is equal to the kinetic energy,[4] both contributing half to the wave energy density E, as can be expected from the equipartition theorem. In ocean waves, surface tension effects are negligible for wavelengths above a few decimetres.
As the waves propagate, their energy is transported. The energy transport velocity is the group velocity. As a result, the wave energy flux, through a vertical plane of unit width perpendicular to the wave propagation direction, is equal to:[10][4]
with cg the group velocity (m/s). Due to the dispersion relation for water waves under the action of gravity, the group velocity depends on the wavelength λ, or equivalently, on the wave period T. Further, the dispersion relation is a function of the water depth h. As a result, the group velocity behaves differently in the limits of deep and shallow water, and at intermediate depths:[4][6]
| Properties of gravity waves on the surface of deep water, shallow water and at intermediate depth, according to linear wave theory | |||||
|---|---|---|---|---|---|
| quantity | symbol | units | deep water ( h > ½ λ ) |
shallow water ( h < 0.05 λ ) |
intermediate depth ( all λ and h ) |
| phase velocity |  |
m / s |  |
 |
 |
| group velocity[A 2] |  |
m / s |  |
 |
 |
| ratio |  |
- |  |
 |
 |
| wavelength |  |
m |  |
 |
for given period T, the solution of: |
| general | |||||
| wave energy density |  |
J / m2 |  |
||
| wave energy flux |  |
W / m |  |
||
| angular frequency |  |
rad / s | 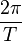 |
||
| wavenumber |  |
rad / m |  |
||
Deep water corresponds with a water depth larger than half the wavelength, which is the common situation in the sea and ocean. In deep water, longer period waves propagate faster and transport their energy faster. The deep-water group velocity is half the phase velocity. In shallow water, for wavelengths larger than twenty times the water depth, as found quite often near the coast, the group velocity is equal to the phase velocity.[5]
[edit] Modern technology
Wave power devices are generally categorized by the method used to capture the energy of the waves. They can also be categorized by location and power take-off system. Method types are point absorber or buoy; surfacing following or attenuator; terminator, lining perpendicular to wave propagation; oscillating water column; and overtopping. Locations are shoreline, nearshore and offshore. Types of power take-off include: hydraulic ram, elastomeric hose pump, pump-to-shore, hydroelectric turbine, air turbine,[11] and linear electrical generator. Some of these designs incorporate parabolic reflectors as a means of increasing the wave energy at the point of capture.
These are descriptions of some wave power systems:
- In the United States, the Pacific Northwest Generating Cooperative is funding the building of a commercial wave-power park at Reedsport, Oregon.[12] The project will utilize the PowerBuoy technology Ocean Power Technologieswhich consists of modular, ocean-going buoys. The rising and falling of the waves moves the buoy-like structure creating mechanical energy which is converted into electricity and transmitted to shore over a submerged transmission line. A 40 kW buoy has a diameter of 12 feet (4 m) and is 52 feet (16 m) long, with approximately 13 feet of the unit rising above the ocean surface. Using the three-point mooring system, they are designed to be installed one to five miles (8 km) offshore in water 100 to 200 feet (60 m) deep.
- An example of a surface following device is the Pelamis Wave Energy Converter. The sections of the device articulate with the movement of the waves, each resisting motion between it and the next section, creating pressurized oil to drive a hydraulic ram which drives a hydraulic motor.[13] The machine is long and narrow (snake-like) and points into the waves; it attenuates the waves, gathering more energy than its narrow profile suggests. Its articulating sections drive internal hydraulic generators (through the use of pumps and accumulators).
- With the Wave Dragon wave energy converter large "arms" focus waves up a ramp into an offshore reservoir. The water returns to the ocean by the force of gravity via hydroelectric generators.
- The AquaBuOY, made by Finavera Renewables Inc., wave energy device: Energy transfer takes place by converting the vertical component of wave kinetic energy into pressurized seawater by means of two-stroke hose pumps. Pressurized seawater is directed into a conversion system consisting of a turbine driving an electrical generator. The power is transmitted to shore by means of a secure, undersea transmission line. A commercial wave power production facility utilizing the AquaBuOY technology is beginning initial construction in Portugal.[14] The company has 250 MW of projects planned or under development on the west coast of North America.[15]
- The SeaRaser, build by Alvin Smith; which uses a entirely new technique (pumping) for gathering the wave energy. [16]
- A device called CETO, currently being tested off Fremantle, Western Australia,[17] consists of a single piston pump attached to the sea floor, with a float tethered to the piston. Waves cause the float to rise and fall, generating pressurized water, which is piped to an onshore facility to drive hydraulic generators or run reverse osmosis water desalination.[18]
- Another type of wave buoys,using special polymeres, is being developed by SRI [19]
[edit] Challenges
These are some of the challenges to deploying wave power devices:
- Efficiently converting wave motion into electricity; generally speaking, wave power is available in low-speed, high forces, and the motion of forces is not in a single direction. Most readily-available electric generators operate at higher speeds, and most readily-available turbines require a constant, steady flow.
- Constructing devices that can survive storm damage and saltwater corrosion; likely sources of failure include seized bearings, broken welds, and snapped mooring lines. Knowing this, designers may create prototypes that are so overbuilt that materials costs prohibit affordable production.
- High total cost of electricity; wave power will only be competitive when the total cost of generation is reduced. The total cost includes the primary converter, the power takeoff system, the mooring system, installation & maintenance cost, and electricity delivery costs.
- Impacts on the marine environment, such as noise pollution, could have negative impact if not monitored, although the noise and visible impact of each design varies greatly.[8]
- In terms of socio-economic challenges, wave farms can result in displacement of commercial and recreational fishermen from productive fishing grounds, can change the pattern of beach sand nourishment, and may represent hazards to safe navigation.[20]
- In the US, development of wave farms is currently hindered by a maze of state and federal regulatory hurdles and limited R&D funding.
[edit] Wave farms
The world's first commercial wave farm opened in 2008 at the Aguçadora Wave Park near Póvoa de Varzim in Portugal. It uses three Pelamis P-750 machines with a total installed capacity of 2.25MW.[3][21] A second phase of the project is now planned to increase the installed capacity to 21MW using a further 25 Pelamis machines.[22]
Funding for a 3MW wave farm in Scotland was announced on February 20, 2007 by the Scottish Executive, at a cost of over 4 million pounds, as part of a £13 million funding packages for marine power in Scotland. The farm will be the world's largest with a capacity of 3MW generated by four Pelamis machines.[23]
Funding has also been announced for the development of a Wave hub off the north coast of Cornwall, England. The Wave hub will act as giant extension cable, allowing arrays of wave energy generating devices to be connected to the electricity grid. The Wave hub will initially allow 20MW of capacity to be connected with potential expansion to 40MW. Four device manufacturers have so far expressed interest in connecting to the Wave hub.
The scientists have calculated that wave energy gathered at Wave Hub will be enough to power up to 7,500 households. Savings that the Cornwall wave power generator will bring are significant: about 300,000 tons of carbon dioxide in the next 25 years.[24]
A CETO wave farm of the coast of Western Australia has been operating to prove commercial viability and after preliminary environmental approval is poised for further development. One benefit of CETO is that the buoys that capture the wave motion are submersed and therefore, are not a visual pollutant. Furthermore, the underwater deployment makes them less prone to storm damage.
[edit] Discussion of Salter's Duck
While historic references to the power of waves do exist, the modern scientific pursuit of wave energy was begun in the 1970s by Professor Stephen Salter of the University of Edinburgh, Scotland in response to the Oil Crisis. His 1974 invention became known as Salter's Duck or Nodding Duck, although it was officially referred to as the Edinburgh Duck. In small scale controlled tests, the Duck's curved cam-like body can stop 90% of wave motion and can convert 90% of that to electricity.[25] The machine has never gone to sea, primarily because its complex hydraulic system is not well suited to incremental implementation, and the costs and risks of a full-scale test would be high. Most of the designs being tested currently absorb far less of the available wave power, and as a result their Mass to Power Ratios remain far away from the theoretical maximum.
According to sworn testimony before the House of Parliament, The UK Wave Energy program was shut down on March 19, 1982, in a closed meeting,[26] the details of which remain secret. The members of the meeting were recruited largely from the nuclear and fossil fuels industries, and the wave programme manager, Clive Grove-Palmer, was excluded.
An analysis of Salter's Duck resulted in a miscalculation of the estimated cost of energy production by a factor of 10,[27] an error which was only recently identified. Some wave power advocates believe that this error, combined with a general lack of enthusiasm for renewable energy in the 1980s (after oil prices fell), hindered the advancement of wave power technology.[28]
[edit] Potential
Deep water wave power resources are truly enormous, between 1 TW and 10 TW, but it is not practical to capture all of this.[29] The useful world-wide resource has been estimated to be greater than 2 TW.[30][31] Locations with the most potential for wave power include; the western seaboard of Europe, the northern coast of the UK and the Pacific coastlines of North and South America, Southern Africa, Australia and New Zealand. The north and south temperate zones have the best sites for capturing wave power. The prevailing westerlies in these zones blow strongest in winter.
The UK has an estimated recoverable resource of between 50–90TWh of electricity a year, this is roughly 15–25% of the current UK electricity demand.[32]
[edit] Patents
- U.S. Patent 3,928,967 — Apparatus and method of extracting wave energy - The original "Salter's Duck" patent
- U.S. Patent 4,134,023 — Apparatus for use in the extraction of energy from waves on water - Salter's method for improving "duck" efficiency
- U.S. Patent 6,194,815 — Piezoelectric rotary electrical energy generator
- U.S. Patent Application 20040217597 — Wave energy converters utilizing pressure differences
[edit] See also
[edit] Notes
- ^ For a small-amplitude sinusoidal wave
 with wave amplitude
with wave amplitude  the wave energy density per unit horizontal area is
the wave energy density per unit horizontal area is  or
or  using the wave height
using the wave height  for sinusoidal waves. In terms of the variance of the surface elevation
for sinusoidal waves. In terms of the variance of the surface elevation  the energy density is
the energy density is  . Turning to random waves, the last formulation of the wave energy equation in terms of
. Turning to random waves, the last formulation of the wave energy equation in terms of  is also valid (Holthuijsen, 2007, p. 40), due to Parseval's theorem. Further, the significant wave height is defined as
is also valid (Holthuijsen, 2007, p. 40), due to Parseval's theorem. Further, the significant wave height is defined as  , leading to the factor 1⁄16 in the wave energy density per unit horizontal area.
, leading to the factor 1⁄16 in the wave energy density per unit horizontal area. - ^ For determining the group velocity the angular frequency ω is considered as a function of the wavenumber k, or equivalently, the period T as a function of the wavelength λ.
[edit] References
- ^ Christine Miller (August 2004). "Wave and Tidal Energy Experiments in San Francisco and Santa Cruz". http://www.outsidelands.org/wave-tidal3.php. Retrieved on 2008-08-16.
- ^ Emily Ford. "Wave power scientist enthused by green energy". The Times. http://www.timesonline.co.uk/tol/life_and_style/career_and_jobs/careers_in/careers_in_science/article4111684.ece. Retrieved on 2008-10-15.
- ^ a b Alok Jha (25 September 2008). "Making waves: UK firm harnesses power of the sea ... in Portugal". The Guardian. http://www.guardian.co.uk/technology/2008/sep/25/greentech.alternativeenergy. Retrieved on 2008-10-09.
- ^ a b c d e f Phillips, O.M. (1977). The dynamics of the upper ocean (2nd edition ed.). Cambridge University Press. ISBN 0 521 29801 6.
- ^ a b R. G. Dean and R. A. Dalrymple (1991). Water wave mechanics for engineers and scientists. Advanced Series on Ocean Engineering. 2. World Scientific, Singapore. ISBN 978-9810204204. See page 64–65.
- ^ a b c Goda, Y. (2000). Random Seas and Design of Maritime Structures. World Scientific. ISBN 978 981 02 3256 6.
- ^ "Wave Power". University of Strathclyde. http://www.esru.strath.ac.uk/EandE/Web_sites/01-02/RE_info/wave%20power.htm. Retrieved on 2008-11-02.
- ^ a b "Wave Energy Potential on the U.S. Outer Continental Shelf" (PDF). United States Department of the Interior. http://www.ocsenergy.anl.gov/documents/docs/OCS_EIS_WhitePaper_Wave.pdf. Retrieved on 2008-10-17.
- ^ Holthuijsen, Leo H. (2007). Waves in oceanic and coastal waters. Cambridge: Cambridge University Press. ISBN 0521860288.
- ^ Reynolds, O. (1877). "On the rate of progression of groups of waves and the rate at which energy is transmitted by waves". Nature 16: 343–44.
Lord Rayleigh (J. W. Strutt) (1877). "On progressive waves". Proceedings of the London Mathematical Society 9: 21–26. doi:. Reprinted as Appendix in: Theory of Sound 1, MacMillan, 2nd revised edition, 1894. - ^ Embedded Shoreline Devices and Uses as Power Generation Sources Kimball, Kelly, November 2003
- ^ "Agreement to Develop Wave Power Park in Oregon". www.renewableeneregyaccess.com. http://www.renewableenergyaccess.com/rea/news/story?id=47546. Retrieved on 2008-10-15.
- ^ Jenny Haworth (24 September 2008). "If Portugal can rule the waves, why not Scotland?". The Scotsman. http://news.scotsman.com/opinion/If-Portugal-can-rule-the.4520629.jp. Retrieved on 2008-10-09.
- ^ Wave Energy: Figueira da Foz, Portugal Finavera Renewables
- ^ Wave Energy Device Deployed
- ^ SeaRaser
- ^ Stephen Cauchi (October 5, 2008). "New wave of power in renewable energy market". The Age. http://www.theage.com.au/national/new-wave-of-power-in-renewable-energy-market-20081004-4tyd.html. Retrieved on 2008-10-10.
- ^ "CETO Overview". carnegiecorp.com.au. http://www.carnegiecorp.com.au/index.php?url=/ceto/ceto-overview. Retrieved on 2008-11-03.
- ^ SRI Demonstrates Ocean Wave-Powered Generator off California Coast, SRI International, 08.12.2008
- ^ Steven Hackett. "Economic and Social Considerations for Wave Energy Development in California. In P. Nelson and L. Engeman (eds.), Developing Wave Energy in Coastal California: Socio-Economic and Environmental Effects. Report CEC-500-2008-083". California Energy Commission. http://www.resources.ca.gov/copc/docs/ca_wec_effects.pdf. Retrieved on 2008-12-14.
- ^ "Portugal Goverenment". http://www.portugal.gov.pt/portal/pt/comunicacao/agenda/20080923.htm. Retrieved on 2008-09-24.
- ^ Joao Lima. "Babcock, EDP and Efacec to Collaborate on Wave Energy Projects". Bloomberg Television. http://www.bloomberg.com/apps/news?pid=20601081&sid=aSsaOB9qbiKE&refer=australia. Retrieved on 2008-09-24.
- ^ "Orkney to get 'biggest' wave farm". BBC News. http://news.bbc.co.uk/2/hi/uk_news/scotland/6377423.stm. Retrieved on 2008-10-22.
- ^ "Go-ahead for £28m Cornish wave farm". The Guardian. http://www.guardian.co.uk/environment/2007/sep/17/renewableenergy.uknews. Retrieved on 2008-10-12.
- ^ "Edinburgh Wave Energy Project" (PDF). University of Edinburgh. http://www.mech.ed.ac.uk/research/wavepower/EWPP%20archive/duck%20efficiency%20&%20survival%20notes.pdf. Retrieved on 2008-10-22.
- ^ "Memorandum submitted by Professor S H Salter, Department of Mechanical Engineering, University of Edinburgh". Parliament of the United Kingdom. http://www.parliament.the-stationery-office.co.uk/pa/cm200001/cmselect/cmsctech/291/1031409.htm. Retrieved on 2008-10-22.
- ^ "Water Power Devices". Earth Science Australia. http://www.earthsci.org/mineral/energy/wavpwr/wavepwr.html. Retrieved on 2008-10-22.
- ^ "The untimely death of Salter's Duck". Green Left Weekly. http://www.greenleft.org.au/1992/64/2832. Retrieved on 2008-10-22.
- ^ Engineering Committee on Oceanic Resources — Working Group on Wave Energy Conversion (2003), John Brooke, ed., Wave Energy Conversion, Elsevier, pp. 7, ISBN 0080442129, http://books.google.com/books?id=UGAXRwoLZY4C&dq=John+Brooke,+ed.,+Wave+Energy+Conversion&source=gbs_summary_s&cad=0
- ^ Tom Thorpe. "An Overview of Wave Energy Technologies: Status, Performance and Costs" (PDF). wave-energy.net. http://www.wave-energy.net/Library/An%20Overview%20of%20Wave%20Energy.pdf. Retrieved on 2008-10-13.
- ^ Cruz J.; Gunnar M., Barstow S., Mollison D. (2008), Joao Cruz, ed., Green Energy and Technology, Ocean Wave Energy, Springer Science+Business Media, pp. 93, ISBN 978-3-540-74894-6
- ^ "Pelamis Wave Power". pelamiswave.com. http://www.pelamiswave.com/index.php. Retrieved on 2008-10-13.
[edit] Further reading
- Cruz, Joao (2008), Ocean Wave Energy - Current Status and Future Prospects, Springer, ISBN 3540748946, 431 pp.
- McCormick, Michael (2007), Ocean Wave Energy Conversion, Dover, ISBN 0486462455, 256 pp.
- Twidell, John; Weir, Anthony D.; Weir, Tony (2006), Renewable Energy Resources, Taylor & Francis, ISBN 0419253300, 601 pp.
[edit] External links
| Wikimedia Commons has media related to: Wave power |
| Wikimedia Commons has media related to: Renewable energy |
[edit] News articles and compilations
- Kate Galbraith (September 22, 2008). "Power From the Restless Sea Stirs the Imagination". New York Times. http://www.nytimes.com/2008/09/23/business/23tidal.html?em. Retrieved on 2008-10-09.
- "Wave Power: The Coming Wave" from the Economist, June 5, 2008
- "Is wave power commercially viable?"
- "The untimely death of Salter's Duck"
- "Ocean Power Fights Current Thinking"
- "Wave energy in New Zealand"
- "How it works: Wave power station"
- Waves power future from the Corvallis Gazette Times, February 5, 2005
- EU Wavetrain project — A series of full-text, on-line scientific publications on physical concepts.
- Make the Waves Operate a Motor-Boat Bilge-Pump, Popular Science monthly, February 1919, Unnumbered page, Scanned by Google Books: http://books.google.com/books?id=7igDAAAAMBAJ&pg=PT24
[edit] Wave climate and forecasts
- Information on the long-term statistics of ocean waves can be found at the KNMI wave atlas.
- The US National Oceanic and Atmospheric Administration provides imagery and forecasts of wave height on a global scale. On-line NOAA animation of a user-specified region-of-interest can be set to either wave height or wave period forecasts.
|
||||||||||||||||||||