Taxicab geometry

From Wikipedia, the free encyclopedia

Manhattan distance versus Euclidean distance: The red, blue, and yellow lines have the same length (12) in both Euclidean and taxicab geometry. In Euclidean geometry, the green line has length 6×√2 ≈ 8.48, and is the unique shortest path. In taxicab geometry, the green line's length is still 12, making it no shorter than any other path shown.

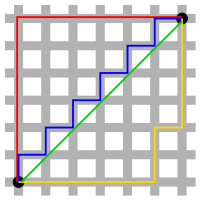
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the (absolute) differences of their coordinates. The taxicab metric is also known as rectilinear distance, L₁ distance or L¹ norm (see L^p space), city block distance, Manhattan distance, or Manhattan length, with corresponding variations in the name of the geometry.^[1] The last name alludes to the grid layout of most streets on the island of Manhattan, which causes the shortest path a car could take between two points in the city to have length equal to the points' distance in taxicab geometry.

[edit] Formal description

The taxicab distance between two points in a Euclidean space with fixed Cartesian coordinate system is the sum of the lengths of the projections of the line segment between the points onto the coordinate axes. For example, in the plane, the taxicab distance between the point P₁ with coordinates (x₁, y₁) and the point P₂ at (x₂, y₂) is |x₁ - x₂| + |y₁ - y₂|.

Taxicab distance depends on the rotation of the coordinate system, but does not depend on its reflection about a coordinate axis or its translation. Taxicab geometry satisfies all of Hilbert's axioms except for the side-angle-side axiom, as one can generate two triangles each with two sides and the angle between them the same, and have them not be congruent.

Circles in discrete and continuous taxicab geometry

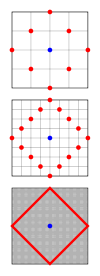
A circle is a set of points with a fixed distance, called the radius, from a point called the center. In taxicab geometry, distance is determined by a different metric than in Euclidean geometry, and the shape of circles changes as well. Taxicab circles are squares with sides oriented at a 45° angle to the coordinate axes. The image to the right shows why this is true, by showing in red the set of all points with a fixed distance from a center, shown in blue. As the size of the city blocks diminishes, the points become more numerous and become a rotated square in a continuous taxicab geometry. While each side would have length √2r using a Euclidean metric, where r is the circle's radius, its length in taxicab geometry is 2r. Thus, a circle's circumference is 8r. The formula for the unit circle in taxicab geometry is |x| + |y| = 1 in Cartesian coordinates and r = 1 / (|sinθ| + |cosθ|) in polar coordinates.

A circle of radius r for the Chebyshev distance (L_∞ metric) on a plane is also a square with side length 2r parallel to the coordinate axes, so planar Chebyshev distance can be viewed as equivalent by rotation and scaling to planar taxicab distance. However, this equivalence between L₁ and L_∞ metrics does not generalize to higher dimensions.

The use of Manhattan distance leads to a strange concept: when the resolution of the Taxicab geometry is made larger, approaching infinity (the size of division of the axis approaches 0), it seems intuitive that the Manhattan distance would approach the Euclidean metric (), but it does not. This is essentially a consequence of being forced to adhere to single-axis movement: when following the Manhattan metric, one cannot move diagonally (in more than one axis simultaneously).

Whenever each pair in a collection of these circles has a nonempty intersection, there exists an intersection point for the whole collection; therefore, the Manhattan distance forms an injective metric space.

A circle of radius 1 (using this distance) is the von Neumann neighborhood of its center.

[edit] Measures of distances in chess

In chess, the distance between squares on the chessboard for rooks is measured in Manhattan distance; kings and queens use Chebyshev distance, and bishops use the Manhattan distance (between squares of the same color) on the chessboard rotated 45 degrees, i.e., with its diagonals as coordinate axes. To reach from one square to another, only kings require the number of moves equal to the distance; rooks, queens and bishops require one or two moves (on an empty board, and assuming that the move is possible at all in the bishop's case).

[edit] See also

• Normed vector space
• Metric
• Orthogonal convex hull
• Hamming distance

[edit] Notes

[edit] References

• Eugene F. Krause (1987). Taxicab Geometry. Dover. ISBN 0-486-25202-7. 

[edit] External links

• City Block Distance, by Kardi Teknomo
• city-block metric on PlanetMath
• Eric W. Weisstein, Taxicab Metric at MathWorld.
• Manhattan distance. Paul E. Black, Dictionary of Algorithms and Data Structures, NIST
• Taxi! - AMS column about Taxicab geometry