Eyeglass prescription
From Wikipedia, the free encyclopedia

An eyeglass prescription is a written order by an optometrist or ophthalmologist to an optician for eyeglasses. It specifies the refractive power to which the eyeglasses are to be made in order to correct blurred vision due to refractive errors, including myopia, hyperopia, astigmatism, and presbyopia. It is typically determined using a phoropter or an automated refractor.
[edit] Abbreviations and terms
Similar to medical prescriptions, eyeglass prescriptions are written on paper pads that frequently contain a number of different abbreviations and terms:
- D.V. is an abbreviation for "distance vision". This specifies the part of the prescription designed primarily to improve far vision. In a bifocal lens, this generally indicates what is to be placed in the top segment.
- N.V. is an abbreviation for "near vision". This may represent a single-vision lens prescription to improve near work, or the reading portion of a bifocal lens. Some prescription forms use "ADD" in place of "N.V." with a single box to indicate the additional refractive power to be added to the spherical of each eye.
- O.D. is an abbreviation for oculus dexter, Latin for "right eye." (Some eyeglass prescriptions simply say "left" and "right" instead of "O.S." and "O.D.") Oculus means "eye" (as in "oculist," an old term for an eye doctor).
- O.S. is an abbreviation for oculus sinister, Latin for "left eye".
- O.U. is an abbreviation for oculi uterque, Latin for "both eyes".
- A spherical correction corrects refractive error of the eye with a single convergent or divergent refractive power in all meridians.
- A cylindrical correction corrects astigmatic refractive error of the eye by adding or subtracting power cylindrically in a meridian specified by the prescribed axis.
- The Axis indicates the angle in degrees of one of two major meridians the prescribed cylindrical power is in. Which major meridian is referenced is indicated by the cylindrical correction being in plus or minus notation. The axis is measured on an imaginary semicircle with a horizontal baseline that starts with zero degrees in the 3 o'clock (or east) direction, and increases to 180 degrees in a counter-clockwise direction.
Most eyeglass prescriptions will contain values here. The "spherical" and "cylindrical" columns contain lens powers in diopters (see below).
- Prism and Base are usually left empty, as they are not seen in most prescriptions. Prism refers to a displacement of the image through the lens, and is used to treat muscular imbalance or other conditions (see vergence dysfunction) that cause errors in eye orientation. Prism correction is measured in "prism diopters", and Base refers to the direction of displacement.
- PD is the distance between pupils, or Pupillary Distance, usually given in millimeters, and written as two values if the prescription is for bifocals or progressive lenses - these are the pupillary distances for the upper and lower lens. They differ due to pupillary convergence when looking at nearby objects.
[edit] Background
Blur is the subjective experience or perception of a defocus aberration within the eye. Blur may appear differently depending on the amount and type of refractive error. The following are some examples of blurred images that may result from refractive errors:
Blur is corrected by focusing light on the retina. This may be done with eyeglasses or contact lenses, or by altering the shape of various eye structures via refractive surgery or special contact lenses.
Eyeglasses sometimes have unwanted effects including magnification or reduction, distortion, color fringes, altered depth perception, etc. Although many people think of lenses as magnifiers, the lenses within eyeglasses improve vision primarily by reducing blur. Depending on the optical setup, they may also produce magnification or reduction of images which may or may not be intentional or desirable.
[edit] Lens power
The values indicated in the "sphere" and "cylinder" columns of an eyeglass prescription specify the optical power of the lenses in diopters, abbreviated D. The higher the number of diopters, the more the lens refracts or bends light. A diopter is the reciprocal of the focal length in meters. If a lens has a focal length of 1/3 meters, it is a 3 diopter lens.
A +10 diopter lens, which has a focal length of 10 centimeters, would make a good magnifying glass. Eyeglass lenses are usually much weaker, because eyeglasses do not work by magnifying; they work by correcting focus. The eye itself has a refractive power of 60 diopters.
Stacking lenses combines their power. A +1 diopter lens combined with a +2 diopter lens forms a +3 diopter system.
Lenses come in positive (plus) and negative (minus) powers. Given that a positive power lens will magnify an object and a negative power lens will reduce it, it is often possible to tell whether a lens is positive or negative by looking through it.
Positive eyeglass lenses can concentrate sunlight.
This series of pictures shows the shadow cast by a pair of 1 diopter drugstore "reading glasses" outdoors in sunlight as we hold it farther and farther away from a wall. As the distance from the wall increases, the shadow of the frame seems to thicken and the bright area in the center gets smaller and brighter. It slowly changes from being "eyeglass-shaped" to circular.
Negative lenses spread sunlight instead of concentrating it.
A negative lens combined with a positive lens removes some of its power. A -2 lens combined with a +5 lens forms a +3 diopter system.
A -3 lens stacked on top of a +3 lens looks almost like flat glass, because the combined power is 0.
In science textbooks, positive lenses are usually diagrammed as convex on both sides; negative lenses are usually diagrammed as concave on both sides. In a real optical system, the best optical quality is usually achieved where most rays of light are roughly normal (i.e., at a right angle) to the lens surface. In the case of an eyeglass lens, this means that the lens should be roughly shaped like a cup with the hollow side toward the eye, so most eyeglass lenses are menisci in shape.
[edit] Spherical lenses and spherical correction
'Usually:
- the "spherical" component is the main correction
- the "cylindrical" component is "fine tuning."'
Depending on the optical setup, lenses can act as magnifiers, lenses can introduce blur, and lenses can correct blur.
Whatever the setup, spherical lenses act equally in all meridians: they magnify, introduce blur, or correct blur the same amount in every direction.
An ordinary magnifying glass is a kind of spherical lens. In a simple spherical lens, each surface is a portion of a sphere. When a spherical lens acts as a magnifier, it magnifies equally in all meridians. Here, note that the magnified letters are magnified both in height and in width.
Similarly, when a spherical lens puts an optical system out of focus and introduces blur, it blurs equally in all meridians:
Here is how this kind of blur looks when viewing an eye chart. This kind of blur involves no astigmatism at all; it is equally blurred in all meridians.
[edit] Amount of refractive error and degree of blur
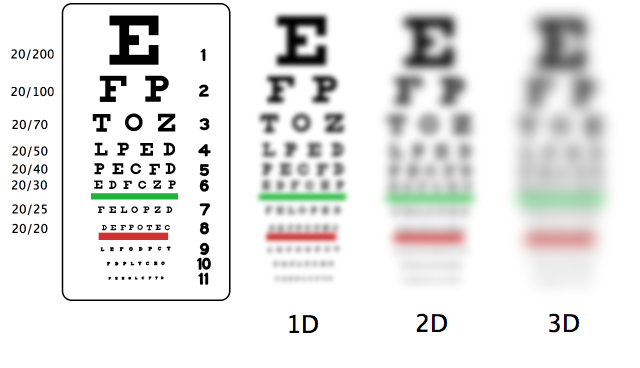
The leftmost image above shows a Snellen eye chart as it might be seen by a person who needs no correction, or by a person who is wearing eyeglasses or contacts that properly correct any refractive errors he or she has.
The images labelled 1D, 2D, and 3D give a very rough impression of the degree of blur that might be seen by someone who has one, two, or three diopters of refractive error. For example, a nearsighted person who needs a -2.0 diopter corrective lens will see something like the 2D image when viewing a standard eye chart at the standard 20-foot distance without glasses.
A very rough rule of thumb is that there is a loss of about one line on an eye chart for each additional 0.25 to 0.5 diopters of refractive error.
The top letter on many eye charts represents 20/200 vision. Many people cannot read even this top letter without glasses. The definition of legal blindness is not based on vision without glasses. The U. S. Social Security administration, for example, states that "we consider you to be legally blind if your vision cannot be corrected to better than 20/200 in your better eye." In other words, what matters in evaluating legal blindness, and for many other purposes, is corrected acuity—which line of the chart can be read with proper lenses. One purpose in which uncorrected vision makes a difference is for receiving a driver's licence that is good without lenses; a person who needs lenses may receive one that requires him to wear the said lenses.
[edit] Cylindrical lenses and cylindrical correction
Some kinds of magnifying glasses, made specifically for reading wide columns of print, are cylindrical lenses. For a simple cylindrical lens, the surfaces of the lens are portions of a cylinder's surface. Consider how this would refract light. When a cylindrical lens acts as a magnifier, it magnifies only in one direction. For example, the magnifier shown magnifies letters only in height, not in width.
Similarly when a cylindrical lens puts an optical system out of focus and introduces blur, it blurs only in one direction.
This is the kind of blur that results from uncorrected astigmatism. The letters are smeared out directionally, as if an artist had rubbed his thumb across a charcoal drawing. A cylindrical lens of the right power can correct this kind of blur. When viewing an eye chart, this is how this kind of blur might appear:
Compare it to the kind of blur that is equally blurred in all directions.
When an eye doctor measures an eye—a procedure known as refraction—usually he begins by finding the best spherical correction. If there is astigmatism, the next step is to compensate it by adding the right amount of cylindrical correction.
[edit] Axis
Spherical lenses have a single power in all meridians of the lens, such as +1.00 D, or −2.50 D.
Astigmatism, however, causes a directional blur. Here are two examples of the kind of blur you get from astigmatism. The letters are smeared out directionally, as if an artist had rubbed his or her thumb across a charcoal drawing.
A cylindrical lens of the right power and orientation can correct this kind of blur. The second example is a little bit more blurred, and needs a stronger cylindrical lens.
But notice that in addition to being smeared more, the second example is smeared out in a different direction.
A spherical lens is the same in all directions; you can turn it around, and it doesn't change the way it magnifies, or the way it blurs:
A cylindrical lens has refractive power in one direction, like a bar reading magnifier. The rotational orientation of that power is indicated in a prescription with an axis notation.
The axis in a prescription describes orientation of the axis of the cylindrical lens. The direction of the axis is in degrees measured anti-clockwise from the horizontal line through the centers of the pupils when viewed from front side of the glasses (i.e. when viewed from the point of view the person making the measurement). It varies from 1 to 180 degrees.
In the illustration below, viewed from the point of view of the person making the measurement, the axis is 20 degees if written in minus notation or 110 deg (at 90 degrees to the negative axis) if written in plus notation.
The total power of a cylindrical lens varies from zero in the axis meridian to its maximal value in the power meridian, 90 degrees away. in the example above the axis meridian is located in the 20th meridian, and the power meridian is located in the 110th meridian.
The total power of a lens with a spherical and cylindrical correction changes accordingly: in the meridian specified by "axis" in the prescription, the power is equal to the value listed under "sphere". As you move around the clock face, the power in a given meridian will get steadily closer to the sum of the values given for sphere and cylinder until you reach the meridian 90 deg from the meridian specified by "axis", where the power is equal to the sum of "sphere" and "cylinder".
[edit] Spherical Equivalent Refraction
Ophthalmologists and optometrists use the term Spherical Equivalent Refraction (SER) to refer to an eye's effective focusing power if only spherical aberration was present. SER can be defined as:
SER = (SPHERE) + 0.5 * (CYLINDER)
[edit] Distant vision and near vision
The DV portion of the prescription describes the corrections for distant vision. For most people under forty years of age, this is the only part of the prescription that is filled in. The NV or near-vision portion of the prescription is blank because a separate correction for near vision is not needed.
The NV portion is used in prescriptions for bifocals.
In younger people, the lens of the eye is still flexible enough to accommodate over a wide range of distances. With age, the lens hardens and becomes less and less able to accommodate.
This is called "presbyopia"; the presby- root means "old" or "elder". (It is the same root as in the words priest and presbyterian.)
The hardening of the lens is a continuous process, not something that suddenly happens in middle age. It is occurring all along. All that happens around middle age is that the process progresses to the point where it starts to interfere with reading. Therefore almost everybody needs glasses for reading from the age of 40-45.
Because young children have a wider range of accommodation than adults, they sometimes examine objects by holding them much closer to the eye than an adult would.
This chart (which is approximate) shows that a schoolchild has over ten diopters of accommodation, while a fifty-year-old has only two. This means that a schoolchild is able to focus on an object about 10 cm. (4") from the eye, a task for which an adult needs a magnifying glass with a rated power of about 3.5X.
The NV correction due to presbyopia can be predicted using the parameter age only. The accuracy of such a prediction is sufficient in many practical cases, especially when the total correction is less than 3 diopters. See also the following calculator for computing this correction.
[edit] Variations in prescription writing
There is a surprising amount of variation in the way prescriptions are written; the layout and terminology used is not uniform.
When no correction is needed, the spherical power will sometimes be written as "0.00" and sometimes as "Plano" or "Pl". The lens, although not flat, is optically equivalent to a flat piece of glass, and has no refractive power.
When cylindrical correction is needed, the mathematics used to denote the combination of spherical and cylindrical power in a lens can be notated two different ways to indicate the same correction. One is called the plus-cylinder notation and the other the minus-cylinder notation.
These two prescriptions are equivalent:
| Spherical | Cylindrical | Axis |
|---|---|---|
| +2.00 | +1.00 | 090 |
| +3.00 | −1.00 | 180 |
Both of them specify a power of +2.00 diopters at the 90th (vertical) meridian and +3.00 diopters at the 180th (horizontal) meridian.
The first one specifies a +2.00 spherical component, which, by itself, would give a power of +2.00 diopters in all meridians, and adds a +1.00 cylindrical component at 180 degrees (perpendicular to the axis indicated on the prescription, as explained under Axis). The result is +2.00 diopters at the 90th meridian and 2.00 + 1.00 = +3.00 diopters at the 180th meridian.
The second specifies a +3.00 spherical component, which by itself would give a power of +3.00 diopters in all meridians, and adds a -1.00 cylindrical component at 90 degrees. The result is 3.00 − 1.00 = +2.00 diopters at the 90th meridian and +3.00 diopters at the 180th meridian.
In practice, Optometrists tend to use minus-cylinder notation, whereas Ophthalmologists tend to prescribe using plus-cylinder notation.