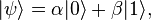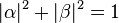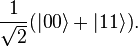bit computer computers computing cryptography cubit design entanglement future math myblog mythmeme physics przeczytać pseudo-telepathy qnd quantum quantum-computing quantum_computing qubit sci/fi science sciences security technology

My tags:

From Wikipedia, the free encyclopedia

A qubit is not to be confused with a cubit, which is an ancient measure of length.

A quantum bit or qubit ['kju.bɪt] (sometimes also qbit) is a unit of quantum information. That information is described by a state vector in a two-level quantum-mechanical system, which is formally equivalent to a two-dimensional vector space over the complex numbers. In addition, the qubit should have these properties^[1]

• scalability (long coherence time)
• can be initialized
• controlled unitary transformations (eg, Rabi oscillations)
• measurable (it has a readout)
• scalable

Contents 1 Bit versus qubit 2 Representation 3 Qubit states 4 Entanglement 4.1 Quantum register 5 Variations of the qubit 6 Physical representation 7 Qubit storage 8 Origin of the term 9 References 10 External links

[edit] Bit versus qubit

A bit is the basic unit of computer information. Regardless of its physical realization, a bit is always understood to be either a 0 or a 1. An analogy to this is a light switch—the down position can represent 0 (normally equated to off) and the up position can represent 1 (normally equated to on).

A qubit has some similarities to a classical bit, but is overall very different. Like a bit, a qubit can have two possible values—normally a 0 or a 1. The difference is that whereas a bit must be either 0 or 1, a qubit can be 0, 1, or a superposition of both.

[edit] Representation

The states a qubit may be measured in are known as basis states (or vectors). As is the tradition with any sort of quantum states, Dirac, or bra-ket notation is used to represent them. This means that the two computational basis states are conventionally written as and (pronounced "ket 0" and "ket 1").

[edit] Qubit states

A pure qubit state is a linear superposition of those two states. This means that the qubit can be represented as a linear combination of and  :

where α and β are probability amplitudes and can in general both be complex numbers.

When we measure this qubit in the standard basis, the probability of outcome is | α | ² and the probability of outcome is | β | ². Because the absolute squares of the amplitudes equate to probabilities, it follows that α and β must be constrained by the equation

simply because this ensures you must measure either one state or the other.

The state space of a single qubit register can be represented geometrically by the Bloch sphere. This is a two-dimensional space which has an underlying geometry of the surface of a sphere. This essentially means that the single qubit register space has two local degrees of freedom. Represented on such a sphere, a classical bit could lie on only one of the poles.

[edit] Entanglement

An important distinguishing feature between a qubit and a classical bit is that multiple qubits can exhibit quantum entanglement. Entanglement is a nonlocal property that allows a set of qubits to express higher correlation than is possible in classical systems. Take, for example, two entangled qubits in the Bell state

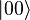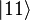In this state, called an equal superposition, there are equal probabilities of measuring either or , as .

Imagine that these two entangled qubits are separated, with one each given to Alice and Bob. Alice makes a measurement of her qubit, obtaining—with equal probabilities—either or . Because of the qubits' entanglement, Bob must now get the exact same measurement as Alice; i.e., if she measures a , Bob must measure the same, as 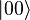is the only state where Alice's qubit is a .

Entanglement also allows multiple states (such as the Bell state mentioned above) to be acted on simultaneously, unlike classical bits that can only have one value at a time. Entanglement is a necessary ingredient of any quantum computation that cannot be done efficiently on a classical computer.

Many of the successes of quantum computation and communication, such as quantum teleportation and superdense coding, make use of entanglement, suggesting that entanglement is a resource that is unique to quantum computation.

[edit] Quantum register

A number of entangled qubits taken together is a qubit register. Quantum computers perform calculations by manipulating qubits within a register.

[edit] Variations of the qubit

Similar to the qubit, a qutrit is a unit of quantum information in a 3-level quantum system. This is analogous to the unit of classical information trit. The term "qudit" is used to denote a unit of quantum information in a d-level quantum system.

[edit] Physical representation

Any two-level system can be used as a qubit. Multilevel systems can be used as well, if they possess two states that can be effectively decoupled from the rest (e.g., ground state and first excited state of a nonlinear oscillator). There are various proposals. Several physical implementations which approximate two-level systems to various degrees were successfully realized. Similarly to a classical bit where the state of a transistor in a processor, the magnetization of a surface in a hard disk and the presence of current in a cable can all be used to represent bits in the same computer, an eventual quantum computer is likely to use various combinations of qubits in its design.

The following is an incomplete list of physical implementations of qubits, and the choices of basis are by convention only.

Physical support	Name	Information support
Single photon (Fock states)	Polarization encoding	Polarization of light	Horizontal	Vertical
	Photon number	Photon number	Vacuum	Single photon state
	Time-bin encoding	Time of arrival	Early	Late
Coherent state of light	Squeezed light	Quadrature	Amplitude-squeezed state	Phase-squeezed state
Electrons	Electronic spin	Spin	Up	Down
	Electron number	Charge	No electron	One electron
Nucleus	Nuclear spin addressed through NMR	Spin	Up	Down
Optical lattices	Atomic spin	Spin	Up	Down
Josephson junction	Superconducting charge qubit	Charge	Uncharged superconducting island (Q=0)	Charged superconducting island (Q=2e, one extra Cooper pair)
	Superconducting flux qubit	Current	Clockwise current	Counterclockwise current
	Superconducting phase qubit	Energy	Ground state	First excited state
Singly charged quantum dot pair	Electron localization	Charge	Electron on left dot	Electron on right dot
Quantum dot	Dot spin	Spin	Down	Up

[edit] Qubit storage

In a paper entitled: “Solid-state quantum memory using the ³¹P nuclear spin,” published in the October 23, 2008 issue of the journal Nature^[2], an international team of scientists that included researchers with the U.S. Department of Energy’s Lawrence Berkeley National Laboratory (Berkeley Lab) reported the first relatively long (1.75 segs.) and coherent transfer of a superposition state in an electron spin 'processing' qubit to a nuclear spin 'memory' qubit. This event can be considered the first relatively consistent quantum Data storage, a vital step towards the development of quantum computing.

[edit] Origin of the term

The origin of the term qubit is attributed to a paper by Benjamin Schumacher.^[3] In the acknowledgments of his paper, Schumacher states that the term qubit was invented in jest, during a conversation with William Wootters. The paper describes a way of compressing states emitted by a quantum source of information so that they require fewer physical resources to store. This procedure is now known as Schumacher compression.

[edit] References

[edit] External links

• An update on qubits in the Oct 2005 issue of Scientific American
• Qubit.org cofounded by one of the pioneers in quantum computation, David Deutsch

v • d • e Quantum computing General Qubit • Quantum computer • Quantum information • Quantum programming • Quantum virtual machine • Timeline of quantum computing • Topological computing Quantum communication Quantum channel • Quantum cryptography • Quantum teleportation • LOCC • Entanglement distillation Quantum algorithms Universal quantum simulator • Deutsch-Jozsa algorithm • Grover's search • Shor's factorization • Simon's Algorithm • (BQP) Quantum computing models Quantum circuit (quantum gate) • One-way quantum computer (cluster state) • Adiabatic quantum computation Decoherence prevention Quantum error correction • Topological quantum computer Physical implementations Quantum optics Linear optics QC • Cavity QED Ultracold atoms Trapped ion quantum computer • Optical lattice Spin-based Nuclear magnetic resonance (NMR) quantum computing • Kane QC • Loss-DiVincenzo (quantum dot) QC Other Superconducting quantum computing (Charge qubit • Flux qubit) • Nitrogen-vacancy center