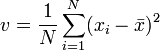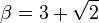Beta distribution
From Wikipedia, the free encyclopedia
Probability density function |
|
Cumulative distribution function |
|
| Parameters | α > 0 shape (real) β > 0 shape (real) |
|---|---|
| Support | ![x \in [0; 1]\!](http://upload.wikimedia.org/math/b/e/4/be450cd15463fbfc4e95de5eb88b6e90.png) |
| Probability density function (pdf) | 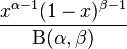 |
| Cumulative distribution function (cdf) |  |
| Mean |  |
| Median | |
| Mode |  for α > 1,β > 1 for α > 1,β > 1 |
| Variance |  |
| Skewness |  |
| Excess kurtosis | see text |
| Entropy | see text |
| Moment-generating function (mgf) |  |
| Characteristic function |  |
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parameterized by two positive shape parameters, typically denoted by α and β. It is the special case of the Dirichlet distribution with only two parameters. Since the Dirichlet distribution is the conjugate prior of the multinomial distribution, the beta distribution is the conjugate prior of the binomial distribution. In Bayesian statistics, it can be seen as the posterior distribution of the parameter p of a binomial distribution after observing α − 1 independent events with probability p and β − 1 with probability 1 − p, if the prior distribution of p was uniform.
Contents |
[edit] Characterization
[edit] Probability density function
The probability density function of the beta distribution is:
where Γ is the gamma function. The beta function, B, appears as a normalization constant to ensure that the total probability integrates to unity.
[edit] Cumulative distribution function
The cumulative distribution function is
where Bx(α,β) is the incomplete beta function and Ix(α,β) is the regularized incomplete beta function.
[edit] Properties
[edit] Moments
The expected value, second moment and variance of a beta random variable X with parameters α and β are given by the formulae:
The skewness is
The kurtosis excess is:
In general, the kth raw moment is given by
which can also be written in a recursive form as
[edit] Quantities of information
Given two beta distributed random variables, X ~ Beta(α, β) and Y ~ Beta(α', β'), the information entropy of X is
where ψ is the digamma function.
The cross entropy is
It follows that the Kullback-Leibler divergence between these two beta distributions is
[edit] Shapes
The beta density function can take on different shapes depending on the values of the two parameters:
 is the uniform [0,1] distribution
is the uniform [0,1] distribution is U-shaped (red plot)
is U-shaped (red plot) or
or  is strictly decreasing (blue plot)
is strictly decreasing (blue plot)
 or
or  is strictly increasing (green plot)
is strictly increasing (green plot)
 is strictly convex
is strictly convex is a straight line
is a straight line is strictly concave
is strictly concave
 is unimodal (purple & black plots)
is unimodal (purple & black plots)
Moreover, if α = β then the density function is symmetric about 1/2 (red & purple plots).
[edit] Parameter estimation
Let
be the sample mean and
be the sample variance. The method-of-moments estimates of the parameters are
If the distribution is required over an interval other than [0, 1], say ![\scriptstyle [\ell,h]](http://upload.wikimedia.org/math/6/a/6/6a61ed6e17822a3dea738dd370552cbe.png) , then replace
, then replace 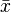 with
with  and
and 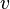 with
with  in the above equations.[1][2]
in the above equations.[1][2]
[edit] Related distributions
- If X has a beta distribution, then T=X/(1-X) has a "beta distribution of the second kind", also called the beta prime distribution.
- The connection with the binomial distribution is mentioned below.
- The Beta(1,1) distribution is identical to the standard uniform distribution.
- If X and Y are independently distributed Gamma(α, θ) and Gamma(β, θ) respectively, then X / (X + Y) is distributed Beta(α,β).
- If X and Y are independently distributed Beta(α,β) and F(2β,2α) (Snedecor's F distribution with 2β and 2α degrees of freedom), then Pr(X ≤ α/(α+xβ)) = Pr(Y > x) for all x > 0.
- The beta distribution is a special case of the Dirichlet distribution for only two parameters.
- The Kumaraswamy distribution resembles the beta distribution.
- If
![X \sim {\rm U}(0, 1]\,](http://upload.wikimedia.org/math/7/4/8/7487f663a469da4699b115cf58b4ce93.png) has a uniform distribution, then
has a uniform distribution, then 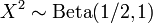 or for the 4 parameter case,
or for the 4 parameter case,  which is a special case of the Beta distribution called the power-function distribution.
which is a special case of the Beta distribution called the power-function distribution. - Binomial opinions in subjective logic are equivalent to Beta distributions.
[edit] Applications
Beta(i, j) with integer values of i and j is the distribution of the i-th order statistic (the i-th smallest value) of a sample of i + j − 1 independent random variables uniformly distributed between 0 and 1. The cumulative probability from 0 to x is thus the probability that the i-th smallest value is less than x, in other words, it is the probability that at least i of the random variables are less than x, a probability given by summing over the binomial distribution with its p parameter set to x. This shows the intimate connection between the beta distribution and the binomial distribution.
Beta distributions are used extensively in Bayesian statistics, since beta distributions provide a family of conjugate prior distributions for binomial (including Bernoulli) and geometric distributions. The Beta(0,0) distribution is an improper prior and sometimes used to represent ignorance of parameter values.
The beta distribution can be used to model events which are constrained to take place within an interval defined by a minimum and maximum value. For this reason, the beta distribution — along with the triangular distribution — is used extensively in PERT, critical path method (CPM) and other project management / control systems to describe the time to completion of a task. In project management, shorthand computations are widely used to estimate the mean and standard deviation of the beta distribution:
where a is the minimum, c is the maximum, and b is the most likely value.
These approximations are exact only for particular values of α and β, specifically when[3]:
or vice versa.
These are notably poor approximations for most other beta distributions exhibiting average errors of 40% in the mean and 549% in the variance[4][5][6]
[edit] Information Theory
We introduce one exemplary use of beta distribution in information theory, particularly for the information theoretic performance analysis for a communication system. In sensor array systems, the distribution of two vector production is used for the performance estimation in frequent. Assume that s and v are vectors the (M-1)-dimensional nullspace of h with isotropic i.i.d. where s, v and h are in CM and the elements of h are i.i.d complex Gaussian random values. Then, the production of s and v with absolute of the result |sHv| is beta(1,M-2) distributed.
[edit] Rule of succession
A classic application of the beta distribution is the rule of succession, introduced in the 18th century by Pierre-Simon Laplace in the course of treating the sunrise problem: it states that, given s successes in n conditionally independent Bernoulli trials with probability p, that p should be estimated as  , as this is the expected value of the beta distribution, starting with a uniform prior and observing s successes in n trials.
, as this is the expected value of the beta distribution, starting with a uniform prior and observing s successes in n trials.
[edit] Four parameters
A beta distribution with the two shape parameters α and β is supported on the range [0,1]. It is possible to alter the location and scale of the distribution by introducing two further parameters representing the minimum and maximum values of the distribution.[7]
[edit] References
- ^ Engineering Statistics Handbook
- ^ Brighton Webs Ltd. Data & Analysis Services for Industry & Education
- ^ Grubbs, Frank E. (1962). Attempts to Validate Certain PERT Statistics or ‘Picking on PERT’. Operations Research 10(6), p. 912-915.
- ^ Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1986-1091.
- ^ Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595-609.
- ^ DRMI Newsletter, Issue 12, April 8, 2005
- ^ Beta4 distribution
[edit] External links
- Eric W. Weisstein, Beta Distribution at MathWorld.
- "Beta Distribution" by Fiona Maclachlan, the Wolfram Demonstrations Project, 2007.
- Beta Distribution - Overview and Example, xycoon.com
- Beta Distribution, brighton-webs.co.uk

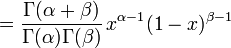










 is strictly
is strictly  is a straight line
is a straight line is strictly
is strictly