Bin packing problem
From Wikipedia, the free encyclopedia
 |
Please help improve this article or section by expanding it. Further information might be found on the talk page. (November 2008) |
 |
This article is in need of attention from an expert on the subject. WikiProject Computer Science or the Computer Science Portal may be able to help recruit one. (November 2008) |
In computational complexity theory, the bin packing problem is a combinatorial NP-hard problem. In it, objects of different volumes must be packed into a finite number of bins of capacity V in a way that minimizes the number of bins used.
There are many variations of this problem, such as 2D packing, linear packing, packing by weight, packing by cost, and so on. They have many applications, such as filling up containers, loading trucks with weight capacity, and creating file backup in removable media.
Since it is NP-hard, the most efficient known algorithms use heuristics to accomplish results which, though very good in most cases, may not be the optimal solution. For example, the first fit algorithm provides a fast but often nonoptimal solution, involving placing each item into the first bin in which it will fit. It requires Θ(n log n) time, where n is the number of elements to be packed. The algorithm can be made much more effective by first sorting the list of elements into decreasing order (sometimes known as the first-fit decreasing algorithm), although this does not guarantee an optimal solution, and for longer lists may increase the running time of the algorithm.
Contents |
[edit] Formal statement
Given a bin size V and a list 
of sizes of the items to pack, find an integer B and a B-partition 
of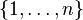 
such that 
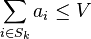for all 
A solution is optimal if it has minimal B. The B-value for an optimal solution is denoted OPT below.
[edit] Analysis of heuristic algorithms
The best fit decreasing and first fit decreasing strategies are among the simplest heuristic algorithms for solving the bin packing problem. They have been shown to use no more than 11/9 OPT + 1 bins (where OPT is the number of bins given by the optimal solution).[1] The simpler of these, the First Fit Decreasing strategy, operates by first sorting the items to be inserted in decreasing order by volume, and then inserting each item into the first bin in the list with sufficient remaining space. The sorting step is relatively expensive, but without it we only achieve the looser bound of 17/10 OPT + 2. Recently, it was proved that the bound 11/9 OPT + 6/9 for FFD is tight.[2] MFFD[3] (a variant of FFD) uses no more than 71/60 OPT + 1 bins[4] (i.e. bounded by about 1.18×opt, compared to about 1.22×opt for FFD).
Although these simple strategies are often good enough, efficient approximation algorithms have been demonstrated[5][6] that can solve the bin packing problem within any fixed percentage of the optimal solution for sufficiently large inputs (this is called an asymptotic polynomial-time approximation scheme). This is an advantage the problem has over many other common NP-hard problems, some of which cannot be approximated within any constant factor at all.
[edit] See also
- Knapsack problem
- Packing problem
- Partition problem
- Multiprocessor scheduling problem
- Subset sum problem
[edit] Notes
- ^ M. Yue, "A simple proof of the inequality FFD(L) ≤ (11/9)OPT(L) + 1, for all L, for the FFD bin-packing algorithm", Acta Mathematicae Applicatae Sinica 7 (1991), pp. 321–331.
- ^ György Dósa, "The Tight Bound of First Fit Decreasing Bin-Packing Algorithm Is FFD(I)≤(11/9)OPT(I)+6/9", ESCAPE 2007, Springer LNCS 4614 (2007), pp. 1–11.
- ^ Michael R. Garey and David S. Johnson, "A 71/60 theorem for bin packing", Journal of Complexity, Vol. 1 (1985), pp. 65–106.
- ^ Yue Minyi and Zhang Lei, "A simple proof of the inequality MFFD(L) ≤ 71/60 OPT(L) + 1, L for the MFFD bin-packing algorithm", Acta Mathematicae Applicatae Sinica 11 (1995), pp. 318–330.
- ^ Vijay V. Vazirani, Approximation Algorithms. Springer. ISBN 3-540-65367-8. p. 74.
- ^ W. F. de la Vega and G. S. Lueker, “Bin Packing Can Be Solved within 1+ε in Linear Time,” Combinatorica 1,4, pp. 349-355, 1981.
[edit] References
- Michael R. Garey and David S. Johnson (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. A4.1: SR1, p. 226.
- David S. Johnson, Alan J. Demers, Jeffrey D. Ullman, M. R. Garey, Ronald L. Graham. Worst-Case Performance Bounds for Simple One-Dimensional Packing Algorithms. SICOMP, Volume 3, Issue 4. 1974.
- Lodi A., Martello S., Vigo, D. (2002) Recent advances on two-dimensional bin packing problems. Discrete Appl. Math., Volume 123, p. 379-396
