Packing problem

	Covering-Packing Dualities
Minimum Set Cover	Maximum Set Packing
Minimum Vertex Cover	Maximum Matching
Minimum Edge Cover	Maximum Independent Set

	Part of a series on:
	Puzzles
	Types Guessing game Riddle; Situation puzzle; ; Logic puzzle Dissection puzzle; Induction puzzle; Logic grid puzzle; Self-reference puzzle; ; Mechanical puzzle Combination puzzle; Construction puzzle; Disentanglement puzzle; Lock puzzle; Folding puzzle; Stick puzzle; ; Picture puzzle Hidden object game; Jigsaw puzzle; Reveal the picture game; Sliding puzzle; Tiling puzzle; ; Puzzle video game; Tour puzzle Chess problem; Logic maze; Maze; Transport puzzle; ; Word puzzle Crossword puzzle; ; Metapuzzle;
	Topics Brain teaser; Dilemma; Enigma; Optical illusion; Packing problem; Paradox; Problem solving; Puzzlehunt; Syllogism; Thinking outside the box;
	Lists List of impossible puzzles; List of maze video games; List of Nikoli puzzle types; List of puzzle topics; List of puzzle video games;
	v • d • e

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Packing problems are one area where mathematics meets puzzles (recreational mathematics). Many of these problems stem from real-life problems with packing items.

In a packing problem, you are given:

one or more (usually two- or three-dimensional) containers
several 'goods', some or all of which must be packed into this container

Usually the packing must be without gaps or overlaps, but in some packing problems the overlapping (of goods with each other and/or with the boundary of the container) is allowed but should be minimised. In others, gaps are allowed, but overlaps are not (usually the total area of gaps has to be minimised).

[edit] Problems

There are many different types of packing problems. Usually they involve finding the maximum number of a certain shape that can be packed into a larger, perhaps different shape.

[edit] Packing infinite space

Many of these problems, when the container size is increased in all directions, become equivalent to the problem of packing objects as densely as possible in infinite Euclidean space. This problem is relevant to a number of scientific disciplines, and has received significant attention. The Kepler conjecture postulated an optimal solution for spheres hundreds of years before it was proven correct by Hales. Many other shapes have received attention, including ellipsoids, tetrahedra, icosahedra, and unequal-sphere dimers.

[edit] Spheres into an Euclidean ball

The problem of packing $k$ disjoint open unit balls inside a ball has a simple and complete answer in the $n$ -dimensional Euclidean space if $\scriptstyle k\leq n+1$ , and in an infinite dimensional Hilbert space with no restrictions. It is maybe worth describing it in detail here, to give a flavor of the general problem. 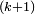In this case, it is available a configuration of $k$ pairwise tangent unit balls (so the centers are the vertices $a 1,.., a k$ of a regular $\scriptstyle(k+1)$ dimensional symplex with edge 2; this is easily realized starting from an orthonormal basis). A small computation shows that the distance of each vertex from the baricenter is 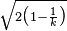$\scriptstyle\sqrt{2\big(1-\frac{1}{k} \big)}$ . Moreover, any other point of the space necessarily has a larger distance from at least one of the $\scriptstyle k$ vertices. 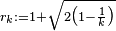In terms of inclusions of balls, this reads: the $\scriptstyle k$ open unit balls centered in $\scriptstyle a_1,..,a_k$ are included in a ball of radius $\scriptstyle r_k:=1+\sqrt{2\big(1-\frac{1}{k}\big)}$ , which is minimal for this configuration. 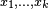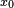To show that the configuration is also optimal, let $\scriptstyle x_1,...,x_k$ be the centers of $\scriptstyle k$ disjoint open unit balls contained in a ball of radius $\scriptstyle r$ centered in a point $\scriptstyle x_0$ . 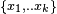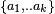Consider the map from the finite set $\scriptstyle\{x_1,..x_k\}$ into $\scriptstyle\{a_1,..a_k\}$ taking $\scriptstyle x_j$ in the corresponding $\scriptstyle a_j$ for each 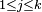$\scriptstyle 1\leq j\leq k$ . 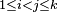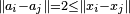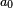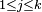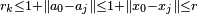Since for all $\scriptstyle 1\leq i<j\leq k$ there holds $\scriptstyle \|a_i-a_j\|=2\leq\|x_i-x_j\|$ this map is 1-Lipschitz and by the Kirszbraun theorem it extends to a 1-Lipschitz map globally defined; in particular, there exists a point $\scriptstyle a_0$ such that for all $\scriptstyle1\leq j\leq k$ one has $\scriptstyle\|a_0-a_j\|\leq\|x_0-x_j\|$ , so that also $\scriptstyle r_k\leq1+\|a_0-a_j\|\leq 1+\|x_0-x_j\|\leq r$ . This shows that there are $\scriptstyle k$ disjoint unit open balls in a ball of radius $\scriptstyle r$ if and only if $\scriptstyle r\geq r_k$ . 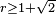Notice that in an infinite dimensional Hilbert space this implies that there are infinitely many disjoint open unit balls inside a ball of radius $\scriptstyle r$ if and only if $\scriptstyle r\geq 1+\sqrt{2}$ . 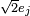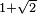For instance, the unit balls centered in $\scriptstyle\sqrt{2}e_j$ , where $\scriptstyle\{e_j\}_j$ is an orthonormal basis, are disjoint and included in a ball of radius $\scriptstyle 1+\sqrt{2}$ centered in the origin. Moreover, for $\scriptstyle r<1+\sqrt{2}$ , the maximum number of disjoint open unit balls inside a ball of radius r is $\scriptstyle\big\lfloor \frac{2}{2-(r-1)^2}\big\rfloor$ .

[edit] Sphere in cuboid

A classic problem is the sphere packing problem, where one must determine how many spherical objects of given diameter d can be packed into a cuboid of size a × b × c.

[edit] Packing circles

There are many other problems involving packing circles into a particular shape of the smallest possible size.

[edit] Hexagonal packing

Circles (and their counterparts in other dimensions) can never be packed with 100% efficiency in dimensions larger than one (in a one dimensional universe, circles merely consist of two points). That is, there will always be unused space if you are only packing circles. The most efficient way of packing circles, hexagonal packing produces approximately 90% efficiency. [1]

[edit] Circles in circle

Some of the more non-trivial circle packing problems are packing unit circles into the smallest possible larger circle.

Minimum solutions:^{[citation needed]}

Number of circles	Circle radius
1	1
2	2
3	2.154...
4	2.414...
5	2.701...
6	3
7	3
8	3.304...
9	3.613...
10	3.813...
11	3.923...
12	4.029...
13	4.236...
14	4.328...
15	4.521...
16	4.615...
17	4.792...
18	4.863...
19	4.863...
20	5.122...

[edit] Circles in square

Pack n unit circles into the smallest possible square.

Minimum solutions:^{[citation needed]}

Number of circles	Square size
1	2
2	3.414...
3	3.931...
4	4
5	4.828...
6	5.328...
7	5.732...
8	5.863...
9	6
10	6.747...
11	7.022...
12	7.144...
13	7.463...
14	7.732...
15	7.863...
16	8
17	8.532...
18	8.656...
19	8.907...
20	8.978...

[edit] Circles in isosceles right triangle

Pack n unit circles into the smallest possible isosceles right triangle (lengths shown are length of leg)

Minimum solutions:^{[citation needed]}

Number of circles	Length
1	3.414...
2	4.828...
3	5.414...
4	6.242...
5	7.146...
6	7.414...
7	8.181...
8	8.692...
9	9.071...
10	9.414...
11	10.059...
12	10.422...
13	10.798...
14	11.141...
15	11.414...

[edit] Circles in equilateral triangle

Pack n unit circles into the smallest possible equilateral triangle (lengths shown are side length).

Minimum solutions:^{[citation needed]}

Number of circles	Length
1	3.464...
2	5.464...
3	5.464...
4	6.928...
5	7.464...
6	7.464...
7	8.928...
8	9.293...
9	9.464...
10	9.464...
11	10.730...
12	10.928...
13	11.406...
14	11.464...
15	11.464...

[edit] Circles in regular hexagon

Pack n unit circles into the smallest possible regular hexagon (lengths shown are side length).

Minimum solutions:^{[citation needed]}

Number of circles	Length
1	1.154...
2	2.154...
3	2.309...
4	2.666...
5	2.999...
6	3.154...
7	3.154...
8	3.709...
9	4.011...
10	4.119...
11	4.309...
12	4.309...
13	4.618...
14	4.666...
15	4.961...

[edit] Packing squares

[edit] Squares in square

A problem is the square packing problem, where one must determine how many squares of side 1 you can pack into a square of side a. Obviously, here if a is an integer, the answer is a², but the precise, or even asymptotic, amount of wasted space for a a non-integer is open.

Proven minimum solutions:^{[citation needed]}

Number of squares

Square size

1

2

3

2

4

2

5

2.707 (2 + 2^−1/2)

6

3

7

3

8

3

9

3

10

3.707 (3 + 2^−1/2)

Other known results:

If you can pack n² − 2 squares in a square of side a, then a ≥ n.^{[citation needed]}
The naive approach (side matches side) leaves wasted space of less than 2a + 1.^{[citation needed]}
The wasted space is asymptotically o(a^7/11).^{[citation needed]}
The wasted space is not asymptotically o(a^1/2).^{[citation needed]}

Walter Stromquist proved that 11 unit squares cannot be packed in a square of side less than 2 + 4×5^−1/2.^{[citation needed]}

[edit] Squares in circle

Pack n squares in the smallest possible circle.

Minimum solutions:^{[citation needed]}

Number of squares	Circle radius
1	0.707...
2	1.118...
3	1.288...
4	1.414...
5	1.581...
6	1.688...
7	1.802...
8	1.978...
9	2.077...
10	2.121...
11	2.215...
12	2.236...

[edit] Tiling

In this type of problem there are to be no gaps, nor overlaps. Most of the time this involves packing rectangles or polyominoes into a larger rectangle or other square-like shape.

[edit] Rectangles in rectangle

There are significant theorems on tiling rectangles (and cuboids) in rectangles (cuboids) with no gaps or overlaps:

Klarner's theorem: An a × b rectangle can be packed with 1 × n strips iff n | a or n | b.

de Bruijn's theorem: A box can be packed with a harmonic brick a × a b × a b c if the box has dimensions a p × a b q × a b c r for some natural numbers p, q, r (i.e., the box is a multiple of the brick.)

When tiling polyominoes, there are two possibilities. One is to tile all the same polyomino, the other possibility is to tile all the possible n-ominoes there are into a certain shape.

[edit] All the same polyominoes in a rectangle

[edit] Different polyominoes

A classic puzzle of this kind is pentomino, where the task is to arrange all twelve pentominoes into rectangles sized 3×20, 4×15, 5×12 or 6×10.

[edit] See also

[edit] References

P. Erdös and R. L. Graham, On Packing Squares with Equal Squares, J. Combin. Theory Ser. A 19 (1975) 119–123.
Eric W. Weisstein, Klarner's Theorem at MathWorld.
Eric W. Weisstein, de Bruijn's Theorem at MathWorld.

[edit] External links

Many puzzle books as well as mathematical journals contain articles on packing problems.

Journal of Recreational Mathematics — easy read, many articles.
Log Stacker
Links to various MathWorld articles on packing
MathWorld notes on packing squares.
Erich's Packing Center
"Box Packing" by Ed Pegg, Jr., the Wolfram Demonstrations Project, 2007.

Packing problem

From Wikipedia, the free encyclopedia

Contents

[edit] Problems

[edit] Packing infinite space

[edit] Spheres into an Euclidean ball

[edit] Sphere in cuboid

[edit] Packing circles

[edit] Hexagonal packing

[edit] Circles in circle

[edit] Circles in square

[edit] Circles in isosceles right triangle

[edit] Circles in equilateral triangle

[edit] Circles in regular hexagon

[edit] Packing squares

[edit] Squares in square

[edit] Squares in circle

[edit] Tiling

[edit] Rectangles in rectangle

[edit] All the same polyominoes in a rectangle

[edit] Different polyominoes

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages

Covering problems	Packing problems
Covering-Packing Dualities
Minimum Set Cover	Maximum Set Packing
Minimum Vertex Cover	Maximum Matching
Minimum Edge Cover	Maximum Independent Set