Binomial coefficient
From Wikipedia, the free encyclopedia

In mathematics, the binomial coefficient  is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n.
is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n.
In combinatorics,  is interpreted as the number of k-element subsets (the k-combinations) of an n-element set, that is the number of ways that k things can be 'chosen' from a set of n things. Hence,
is interpreted as the number of k-element subsets (the k-combinations) of an n-element set, that is the number of ways that k things can be 'chosen' from a set of n things. Hence,  is often read as "n choose k" and is called the choose function of n and k.
is often read as "n choose k" and is called the choose function of n and k.
[edit] Definition
Given a non-negative integer n and an integer k, the binomial coefficient is defined to be the natural number
and
where n! denotes the factorial of n.
Alternatively, a recursive definition can be written as
where
The notation  was introduced by Andreas von Ettingshausen in 1826,[1] although the numbers were already known centuries before that (see Pascal's triangle). Alternative notations include C(n, k), nCk or
was introduced by Andreas von Ettingshausen in 1826,[1] although the numbers were already known centuries before that (see Pascal's triangle). Alternative notations include C(n, k), nCk or  , in all of which the C stands for combinations or choices.
, in all of which the C stands for combinations or choices.
The binomial coefficients are the coefficients of the series expansion of a power of a binomial, hence the name:
If the exponent n is a nonnegative integer then this infinite series is actually a finite sum as all terms with k > n are zero, but if the exponent n is negative or a non-integer, then it is an infinite series. (See the articles on combination and on binomial theorem).
[edit] Combinatorial interpretation
The importance of the binomial coefficients (and the motivation for the alternate name 'choose') lies in the fact that  is the number of ways that k objects can be chosen from among n objects, regardless of order. More formally,
is the number of ways that k objects can be chosen from among n objects, regardless of order. More formally,
 is the number of k-element subsets of an n-element set.
is the number of k-element subsets of an n-element set. 
In fact, this property is often chosen as an alternative definition of the binomial coefficient, since from (1a) one may derive (1) as a corollary by a straightforward combinatorial proof. For a colloquial demonstration, note that in the formula
the numerator gives the number of ways to fill the k slots using the n options, where the slots are distinguishable from one another. Thus a pizza with mushrooms added before sausage is considered to be different from a pizza with sausage added before mushrooms. The denominator eliminates these repetitions because if the k slots are indistinguishable, then all of the k! ways of arranging them are considered identical.
In the context of computer science, it also helps to see  as the number of strings consisting of ones and zeros with k ones and n−k zeros. For each k-element subset, K, of an n-element set, N, the indicator function, 1K : N→{0,1}, where 1K(x) = 1 whenever x in K and 0 otherwise, produces a unique bit string of length n with exactly k ones by feeding 1K with the n elements in a specific order.[2]
as the number of strings consisting of ones and zeros with k ones and n−k zeros. For each k-element subset, K, of an n-element set, N, the indicator function, 1K : N→{0,1}, where 1K(x) = 1 whenever x in K and 0 otherwise, produces a unique bit string of length n with exactly k ones by feeding 1K with the n elements in a specific order.[2]
[edit] Example
The calculation of the binomial coefficient is conveniently arranged like this: ((((5/1)·6)/2)·7)/3 = (((5·6)/2)·7)/3 = ((30/2)·7)/3 = (15·7)/3 = 105/3 = 35, alternately dividing and multiplying with increasing integers. Each division produces an integer result which is itself a binomial coefficient.
[edit] Derivation from binomial expansion
For exponent 1, (1 + x)1 is 1 + x. For exponent 2, (1 + x)2 is (1 + x)·(1 + x), which forms terms as follows. The first factor supplies either a 1 or an x; likewise for the second factor. Thus to form 1, the only possibility is to choose 1 from both factors; To form x2, the only possibility is to choose x from both factors. However, the x term can be formed by 1 from the first and x from the second factor, or x from the first and 1 from the second factor; thus it acquires a coefficient of 2. Proceeding to exponent 3, (1 + x)3 reduces to (1 + x)2·(1 + x), where we already know that (1 + x)2 = 1 + 2x + x2, giving an initial expansion of (1 + x)·(1 + 2x + x2). Again the extremes, 1 and x3 arise in a unique way. However, the x term is either 1·2x or x·1, for a coefficient of 3; likewise x2 arises in two ways, summing the coefficients 2 and 1 to give 3.
This suggests an induction. Thus for exponent n, each term of (1+x)n has n − k factors of 1 and k factors of x. If k is 0 or n, the term xk arises in only one way, and we get the terms 1 and xn. So  and
and  If k is neither 0 nor n, then the term xk arises in (1 + x)n = (1 + x)·(1 + x)n−1 in two ways, from 1·xk and from x·xk−1, summing the coefficients
If k is neither 0 nor n, then the term xk arises in (1 + x)n = (1 + x)·(1 + x)n−1 in two ways, from 1·xk and from x·xk−1, summing the coefficients  to give
to give  . This is the origin of Pascal's triangle, discussed below.
. This is the origin of Pascal's triangle, discussed below.
Another perspective is that to form xk from n factors of (1+x), we must choose x from k of the factors and 1 from the rest. To count the possibilities, consider all n! permutations of the factors. Represent each permutation as a shuffled list of the numbers from 1 to n. Select a 1 from the first n − k factors listed, and an x from the remaining k factors; in this way each permutation contributes to the term xk. For example, the list 〈4,1,2,3〉 selects 1 from factors 4 and 1, and selects x from factors 2 and 3, as one way to form the term x2 like this: "(1 + x)·(1 + x )·(1 + x )·(1 + x)". But the distinct list 〈1,4,3,2〉 makes exactly the same selection; the binomial coefficient formula must remove this redundancy. The n − k factors for 1 have (n − k)! permutations, and the k factors for x have k! permutations. Therefore n!/(n − k)!k! is the number of distinct ways to form the term xk.
A simpler explanation follows: One can pick a random element out of n in exactly n ways, a second random element in n − 1 ways, and so forth. Thus, k elements can be picked out of n in n·(n − 1)···(n − k + 1) ways. In this calculation, however, each order-independent selection occurs k! times, as a list of k elements can be permuted in so many ways. Thus eq. (1) is obtained.
[edit] Pascal's triangle
Pascal's rule is the important recurrence relation
which can be used to prove by mathematical induction that  is a natural number for all n and k, (equivalent to the statement that k! divides the product of k consecutive integers), a fact that is not immediately obvious from formula (1).
is a natural number for all n and k, (equivalent to the statement that k! divides the product of k consecutive integers), a fact that is not immediately obvious from formula (1).
Pascal's rule also gives rise to Pascal's triangle:
-
0: 1 1: 1 1 2: 1 2 1 3: 1 3 3 1 4: 1 4 6 4 1 5: 1 5 10 10 5 1 6: 1 6 15 20 15 6 1 7: 1 7 21 35 35 21 7 1 8: 1 8 28 56 70 56 28 8 1
Row number n contains the numbers  for k = 0,…,n. It is constructed by starting with ones at the outside and then always adding two adjacent numbers and writing the sum directly underneath. This method allows the quick calculation of binomial coefficients without the need for fractions or multiplications. For instance, by looking at row number 5 of the triangle, one can quickly read off that
for k = 0,…,n. It is constructed by starting with ones at the outside and then always adding two adjacent numbers and writing the sum directly underneath. This method allows the quick calculation of binomial coefficients without the need for fractions or multiplications. For instance, by looking at row number 5 of the triangle, one can quickly read off that
- (x + y)5 = 1 x5 + 5 x4y + 10 x3y2 + 10 x2y3 + 5 x y4 + 1 y5.
The differences between elements on other diagonals are the elements in the previous diagonal, as a consequence of the recurrence relation (3) above.
[edit] Combinatorics and statistics
Binomial coefficients are of importance in combinatorics, because they provide ready formulas for certain frequent counting problems:
- There are
 ways to choose k elements from a set of n elements. See Combination.
ways to choose k elements from a set of n elements. See Combination. - There are
 ways to choose k elements from a set of n if repetitions are allowed. See Multiset.
ways to choose k elements from a set of n if repetitions are allowed. See Multiset. - There are
 strings containing k ones and n zeros.
strings containing k ones and n zeros. - There are
 strings consisting of k ones and n zeros such that no two ones are adjacent.
strings consisting of k ones and n zeros such that no two ones are adjacent. - The Catalan numbers are

- The binomial distribution in statistics is

- The formula for a Bézier curve.
[edit] Identities involving binomial coefficients
When n is an integer
This follows from (2) by using (1 + x)n = xn·(1 + x−1)n. It is reflected in the symmetry of Pascal's triangle. A combinatorial interpretation of this formula is as follow: when forming a subset of k elements (from a set of size n), it is equivalent to consider the number of ways you can pick k elements and the number of ways you can exclude n − k elements.
Another formula is
it is obtained from (2) using x = 1. This is equivalent to saying that the elements in one row of Pascal's triangle always add up to two raised to an integer power. A combinatorial interpretation of this fact involving double counting is given by counting subsets of size 0, size 1, size 2, and so on up to size n of a set S of n elements. Since we count the number of subsets of size i for 0 ≤ i ≤ n, this sum must be equal to the number of subsets of S, which is known to be 2n.
The formula
follows from (2), after differentiating with respect to x and then substituting x = 1.
Furthermore,
for all 0 < k < n if and only if n is prime.
We can prove this as follows: When p is prime, p divides
 for all 0 < k < p
for all 0 < k < p
because it is a natural number and the numerator has a prime factor p but the denominator does not have a prime factor p. So  ≡0 (mod p)
≡0 (mod p)
When n is composite, let p be the smallest prime factor of n and let k = n/p. Then 0 < p < n and
otherwise the numerator k(n−1)(n−2)×...×(n−p+1) has to be divisible by n = k×p, this can only be the case when (n−1)(n−2)×...×(n−p+1) is divisible by p. But n is divisible by p, so p does not divide n−1, n−2, ..., n−p+1 and because p is prime, we know that p does not divide (n−1)(n−2)×...×(n−p+1) and so the numerator cannot be divisible by n.
is found by expanding (1 + x)m (1 + x)n−m = (1 + x)n with (2). As  is zero if k > n, the sum is finite for integer n and m. Equation (7a) generalizes equation (3). It holds for arbitrary, complex-valued m and n, the Chu-Vandermonde identity.
is zero if k > n, the sum is finite for integer n and m. Equation (7a) generalizes equation (3). It holds for arbitrary, complex-valued m and n, the Chu-Vandermonde identity.
A related formula is
While equation (7a) is true for all values of m, equation (7b) is true for all values of j.
From expansion (7a) using n=2m, k = m, and (4), one finds
Denote by F(n + 1) the Fibonacci numbers. We obtain a formula about the diagonals of Pascal's triangle
This can be proved by induction using (3).
Also using (3) and induction, one can show that
Again by (3) and induction, one can show that for k = 0, ... , n−1
as well as
which is itself a special case of the result that for any integer k = 1, ..., n − 1,
which can be shown by differentiating (2) k times and setting x = −1.
The infinite series
is convergent for n ≥ 2. It is the limiting case of the finite sum
This formula is proved by mathematical induction on k.
Using (8) one can derive
and
[edit] Identities with combinatorial proofs
Many identities involving binomial coefficients can be proved by combinatorial means. For example, the following identity for nonnegative integers  (which reduces to (6) when q = 1):
(which reduces to (6) when q = 1):
can be given a double counting proof as follows. The left side counts the number of ways of selecting a subset of [n] of at least q elements, and marking q elements among those selected. The right side counts the same parameter, because there are  ways of choosing a set of q marks and they occur in all subsets that additionally contain some subset of the remaining elements, of which there are 2n − q.
ways of choosing a set of q marks and they occur in all subsets that additionally contain some subset of the remaining elements, of which there are 2n − q.
The identity (8) also has a combinatorial proof. The identity reads
Suppose you have 2n empty squares arranged in a row and you want to mark (select) n of them. There are  ways to do this. On the other hand, you may select your n squares by selecting k squares from among the first n and n − k squares from the remaining n squares. This gives
ways to do this. On the other hand, you may select your n squares by selecting k squares from among the first n and n − k squares from the remaining n squares. This gives
Now apply (4) to get the result.
[edit] Generating functions
The binomial coefficients can also be derived from the labelled case of the Fundamental Theorem of Combinatorial Enumeration. This is done by defining C(n,k) to be the number of ways of partitioning [n] into two subsets, the first of which has size k. These partitions form a combinatorial class with the specification
Hence the exponential generating function B of the sum function of the binomial coefficients is given by
This immediately yields
as expected. We mark the first subset with  in order to obtain the binomial coefficients themselves, giving
in order to obtain the binomial coefficients themselves, giving
This yields the bivariate generating function
Extracting coefficients, we find that
or
again as expected. This derivation closely parallels that of the Stirling numbers of the first and second kind, motivating the binomial-style notation that is used for these numbers.
[edit] Divisors of binomial coefficients
The prime divisors of  can be interpreted as follows: if p is a prime number and pr is the highest power of p which divides
can be interpreted as follows: if p is a prime number and pr is the highest power of p which divides  , then r is equal to the number of natural numbers j such that the fractional part of k/pj is bigger than the fractional part of n/pj. In particular,
, then r is equal to the number of natural numbers j such that the fractional part of k/pj is bigger than the fractional part of n/pj. In particular,  is always divisible by n/gcd(n,k).
is always divisible by n/gcd(n,k).
A somewhat surprising result by David Singmaster (1974) is that any integer divides almost all binomial coefficients. More precisely, fix an integer d and let f(N) denote the number of binomial coefficients  with n < N such that d divides
with n < N such that d divides  . Then
. Then
Since the number of binomial coefficients  with n < N is N(N+1) / 2, this implies that the density of binomial coefficients divisible by d goes to 1.
with n < N is N(N+1) / 2, this implies that the density of binomial coefficients divisible by d goes to 1.
[edit] Bounds for binomial coefficients
The following bounds for  hold:
hold:

[edit] Generalizations
[edit] Generalization to multinomials
Binomial coefficients can be generalized to multinomial coefficients. They are defined to be the number:
where
While the binomial coefficients represent the coefficients of (x+y)n, the multinomial coefficients represent the coefficients of the polynomial
- (x1 + x2 + ... + xr)n.
See multinomial theorem. The case r = 2 gives binomial coefficients:
The combinatorial interpretation of multinomial coefficients is distribution of n distinguishable elements over r (distinguishable) containers, each containing exactly ki elements, where i is the index of the container.
Multinomial coefficients have many properties similar to these of binomial coefficients, for example the recurrence relation:
and symmetry:
where (σi) is a permutation of (1,2,...,r).
[edit] Generalization to negative integers
If 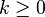 , then
, then  extends to all n.
extends to all n.
The binomial coefficient extends to k < 0 via
Notice in particular, that
This gives rise to the Pascal Hexagon or Pascal Windmill. [3]
[edit] Generalization to real and complex argument
The binomial coefficient  can be defined for any complex number z and any natural number k as follows:
can be defined for any complex number z and any natural number k as follows:
This generalization is known as the generalized binomial coefficient and is used in the formulation of the binomial theorem and satisfies properties (3) and (7).f
Alternatively, the infinite product (cf. Gamma function, alternative definition)
may be used to generalize the binomial coefficient. This formula discloses that asymptotically  and
and  as
as  .
.
The derivative of the generalized binomial coefficient is given by
 .
.
[edit] Interpolation
For k fixed, the expression  is a polynomial in z of degree k with rational coefficients.
is a polynomial in z of degree k with rational coefficients.
p(z) is the unique polynomial of degree k satisfying p(0) = p(1) = ... = p(k − 1) = 0 and p(k) = 1.
Using Stirling numbers of the first kind the series expansion around any arbitrarily chosen point z0 is
For the particular choice z0 = 0 this reduces to
Any polynomial p(z) of degree d can be written in the form
The explicit representation is
This is important in the theory of difference equations and finite differences, and can be seen as a discrete analog of Taylor's theorem. It is closely related to Newton's polynomial. Alternating sums of this form may be expressed as the Nörlund–Rice integral.
In particular, one can express the product of binomial coefficients as such a linear combination:
where the connection coefficients are multinomial coefficients. In terms of labelled combinatorial objects, the connection coefficients represent the number of ways to assign m+n-k labels to a pair of labelled combinatorial objects of weight m and n respectively, that have had their first k labels identified, or glued together, in order to get a new labelled combinatorial object of weight m+n-k. (That is, to separate the labels into 3 portions to be applied to the glued part, the unglued part of the first object, and the unglued part of the second object.) In this regard, binomial coefficients are to exponential generating series what falling factorials are to ordinary generating series.
[edit] Partial Fraction Decomposition
The partial fraction decomposition of the inverse is given by
 and
and 
[edit] Newton's binomial series
Newton's binomial series, named after Sir Isaac Newton, is one of the simplest Newton series:
The identity can be obtained by showing that both sides satisfy the differential equation (1+z) f'(z) = α f(z).
The radius of convergence of this series is 1. An alternative expression is
where the identity
is applied.
The formula for the binomial series was etched onto Newton's gravestone in Westminster Abbey in 1727.
[edit] Two real or complex valued arguments
The binomial coefficient is generalized to two real or complex valued arguments using gamma function or Beta function via
This definition inherits these following additional properties from Γ:
moreover,
 .
.
[edit] Generalization to q-series
The binomial coefficient has a q-analog generalization known as the Gaussian binomial.
[edit] Generalization to infinite cardinals
The definition of the binomial coefficient can be generalized to infinite cardinals by defining:
where A is some set with cardinality α. One can show that the generalized binomial coefficient is well-defined, in the sense that no matter what set we choose to represent the cardinal number α,  will remain the same. For finite cardinals, this definition coincides with the standard definition of the binomial coefficient.
will remain the same. For finite cardinals, this definition coincides with the standard definition of the binomial coefficient.
Assuming the Axiom of Choice, one can show that  for any infinite cardinal α.
for any infinite cardinal α.
[edit] Binomial coefficient in programming languages
The notation 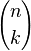 is convenient in handwriting but inconvenient for typewriters and computer terminals. Many programming languages do not offer a standard subroutine for computing the binomial coefficient, but for example the J programming language uses the exclamation mark: k ! n .
is convenient in handwriting but inconvenient for typewriters and computer terminals. Many programming languages do not offer a standard subroutine for computing the binomial coefficient, but for example the J programming language uses the exclamation mark: k ! n .
Naive implementations, such as the following snippet in C:
int choose(int n, int k) {
return factorial(n) / (factorial(k) * factorial(n - k));
}
are prone to overflow errors, severely restricting the range of input values. A direct implementation of the first definition works well:
unsigned long long choose(unsigned n, unsigned k) {
if (k > n)
return 0;
if (k > n/2)
k = n-k; // Take advantage of symmetry
long double accum = 1;
for (unsigned i = 1; i <= k; i++)
accum = accum * (n-k+i) / i;
return accum + 0.5; // avoid rounding error
}
Another way to compute the binomial coefficient when using large numbers is to recognize that
lnΓ(n) is a special function that is easily computed and is standard in some programming languages such as using LogGamma in Mathematica or gammaln in Matlab. Roundoff error may cause the returned value to not be an integer.
[edit] See also
- Combination
- Central binomial coefficient
- Binomial transform
- Table of Newtonian series
- List of factorial and binomial topics
- Multiplicities of entries in Pascal's triangle
- Binomial theorem
- Binomial series
[edit] Notes
- ^ Nicholas J. Higham, Handbook of writing for the mathematical sciences, SIAM. ISBN 0898714206, p. 25
- ^ PlanetMath: binomial coefficient
- ^ Hilton, Holton and Pedersen (1997). Mathematical Reflections. Springer. ISBN 0-387-94770-1.
[edit] References
- This article incorporates material from the following PlanetMath articles, which are licensed under the GFDL: Binomial Coefficient, Bounds for binomial coefficients, Proof that C(n,k) is an integer, Generalized binomial coefficients.
- Knuth, Donald E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms' (Third ed.). Addison-Wesley. pp. 52–74. ISBN 0-201-89683-4.
- Graham, Ronald L.; Knuth, Donald E .; Patashnik, Oren (1989), Concrete Mathematics, Addison Wesley, pp. 153–242, ISBN 0-201-14236-8
- Singmaster, David (1974). "Notes on binomial coefficients. III. Any integer divides almost all binomial coefficients". J. London Math. Soc. (2) 8: 555–560. doi:.
- Bryant, Victor (1993). Aspects of combinatorics. Cambridge University Press.
- Arthur T. Benjamin; Jennifer Quinn, Proofs that Really Count: The Art of Combinatorial Proof , Mathematical Association of America, 2003.



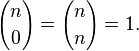




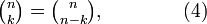





















![\sum_{k=0}^{n} {n \choose k} = n! [z^n] \exp (2z) = 2^n,](http://upload.wikimedia.org/math/f/0/0/f00fca362ff0fd83e6d388b28857706b.png)


![{n \choose k} = n! [u^k] [z^n] \exp uz \exp z =
n! [z^n] \frac{z^k}{k!} \exp z](http://upload.wikimedia.org/math/6/7/7/67750cc47b792757979b1497b888fca7.png)
![\frac{n!}{k!} [z^{n-k}] \exp z =
\frac{n!}{k! \, (n-k)!},](http://upload.wikimedia.org/math/1/c/b/1cbeb2e959939d095ba549acc1b45b0f.png)























