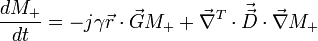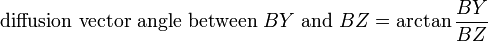Diffusion MRI

From Wikipedia, the free encyclopedia

  (Redirected from Diffusion tensor imaging)
Jump to: navigation, search
DTI Color Map

Diffusion MRI is a magnetic resonance imaging (MRI) method that produces in vivo images of biological tissues weighted with the local microstructural characteristics of water diffusion.

More precisely, the image-intensities at each position are attenuated, depending on the strength (b-value) and direction of the so-called magnetic diffusion gradient, as well as on the local microstructure in which the water molecules diffuse. The more attenuated the image is at a given position, the more diffusion there is in the direction of the diffusion gradient. In order to measure the tissue's complete diffusion profile, one needs to repeat the MR scans, applying different directions (and possibly strengths) of the diffusion gradient for each scan.

Traditionally, in diffusion-weighted imaging (DWI), three gradient-directions are applied, sufficient to estimate the trace of the diffusion tensor or 'average diffusivity', a putative measure of edema. Clinically, trace-weighted images have proven to be very useful to diagnose vascular strokes in the brain, by early detection (within a couple of minutes) of the hypoxic edema.

More extended diffusion tensor imaging (DTI) scans derive neural tract directional information from the data using 3D or multidimensional vector algorithms based on three, six, or more gradient directions, sufficient to compute the diffusion tensor. The diffusion model is a rather simple model of the diffusion process, assuming homogeneity and linearity of the diffusion within each image-voxel. From the diffusion tensor, diffusion anisotropy measures such as the Fractional Anisotropy (FA), can be computed. Moreover, the principal direction of the diffusion tensor can be used to infer the white-matter connectivity of the brain (i.e. tractography; trying to see which part of the brain is connected to which other part).

Recently, more advanced models of the diffusion process have been proposed that aim to overcome the weaknesses of the diffusion tensor model. Amongst others, these include q-space imaging and generalized diffusion tensor imaging.

Contents

[edit] Bloch-Torrey Equation

In 1956, H.C. Torrey mathematically showed how the Bloch equation for magnetization would change with the addition of diffusion.[1] Torrey modified Bloch's original description of transverse magnetization to include diffusion terms and the application of a spatially varying gradient. The Bloch-Torrey equation neglecting relaxation is:

\frac{dM_+}{dt}=-j \gamma \vec r \cdot \vec G M_+ + \vec \nabla^T \cdot \vec {\vec D} \cdot \vec \nabla M_+

For the simplest case where the diffusion is isotropic the diffusion tensor is

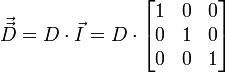\vec {\vec D} = D \cdot \vec I = D \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix},

which means that the Bloch-Torrey equation will have the solution

M_+(\vec r,t)=M_0e^{-\frac{1}{3}D\gamma ^2G^2t^3}e^{-j\gamma \vec r \cdot \int_0^tdt' \vec G(t')}.

This demonstrates a cubic dependence of transverse magnetization on time. Anisotropic diffusion will have a similar solution method, but with a more complex diffusion tensor.

[edit] Diffusion-weighted imaging

Diffusion-weighted imaging is an MRI method that produces in vivo magnetic resonance images of biological tissues weighted with the local characteristics of water diffusion.

DWI is a modification of regular MRI techniques, and is an approach which utilizes the measurement of Brownian motion of molecules. Regular MRI acquisition utilizes the behaviour of protons in water to generate contrast between clinically relevant features of a particular subject. The versatile nature of MRI is due to this capability of producing contrast, called weighting. In a typical T1-weighted image, water molecules in a sample are excited with the imposition of a strong magnetic field. This causes many of the protons in water molecules to precess simultaneously, producing signals in MRI. In T2-weighted images, contrast is produced by measuring the loss of coherence or synchrony between the water protons. When water is in an environment where it can freely tumble, relaxation tends to take longer. In certain clinical situations, this can generate contrast between an area of pathology and the surrounding healthy tissue.

In diffusion-weighted images, instead of a homogeneous magnetic field, the homogeneity is varied linearly by a pulsed field gradient. Since precession is proportional to the magnet strength, the protons begin to precess at different rates, resulting in dispersion of the phase and signal loss. Another gradient pulse is applied in the same direction but with opposite magnitude to refocus or rephase the spins. The refocusing will not be perfect for protons that have moved during the time interval between the pulses, and the signal measured by the MRI machine is reduced. This reduction in signal due to the application of the pulse gradient can be related to the amount of diffusion that is occurring through the following equation:

\frac{S}{S_0} = e^{-\gamma^2 G^2 \delta^2 \left( \Delta - \delta /3 \right) D} = e^{-b D}\,

where S0 is the signal intensity without the diffusion weighting, S is the signal with the gradient, γ is the gyromagnetic ratio, G is the strength of the gradient pulse, δ is the duration of the pulse, Δ is the time between the two pulses, and finally, D is the diffusion constant.

By rearranging the formula to isolate the diffusion-coefficient, it is possible to obtain an idea of the properties of diffusion occurring within a particular voxel (volume picture element). These values, called apparent diffusion coefficient (ADC) can then be mapped as an image, using diffusion as the contrast.

The first successful clinical application of DWI was in imaging the brain following stroke in adults. Areas which were injured during a stroke showed up "darker" on an ADC map compared to healthy tissue. At about the same time as it became evident to researchers that DWI could be used to assess the severity of injury in adult stroke patients, they also noticed that ADC values varied depending on which way the pulse gradient was applied. This orientation-dependent contrast is generated by diffusion anisotropy, meaning that the diffusion in parts of the brain has directionality. This may be useful for determining structures in the brain which could restrict the flow of water in one direction, such as the myelinated axons of nerve cells (which is affected by multiple sclerosis). However, in imaging the brain following a stroke, it may actually prevent the injury from being seen. To compensate for this, it is necessary to apply a mathematical operator, called a tensor, to fully characterize the motion of water in all directions. This tensor is called a diffusion tensor: 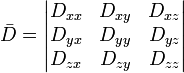\bar{D} = \begin{vmatrix} D_{xx} & D_{xy} & D_{xz} \\ D_{yx} & D_{yy} & D_{yz} \\ D_{zx} & D_{zy} & D_{zz} \end{vmatrix}

Diffusion-weighted images are very useful to diagnose vascular strokes in the brain. Diffusion tensor imaging is being developed for studying the diseases of the white matter of the brain as well as for studies of other body tissues (see below).

[edit] Diffusion tensor imaging

Diffusion tensor imaging (DTI) is a magnetic resonance imaging (MRI) technique that enables the measurement of the restricted diffusion of water in tissue in order to produce neural tract images instead of using this data solely for the purpose of assigning contrast or colors to pixels in a cross sectional image. The idea of using diffusion data to aid in the production of images of neural tracts was first proposed by Aaron Filler & colleagues in March 1991,[2] and several months later the first DTI image showing neural tracts curving through the brain was produced.[3][4] The tensor data for these initial images was obtained using the following sets of formulas:

(\text{vector length})^2 = BX^2 + BY^2 + BZ^2 \,
\text{diffusion vector angle between }BX\text{ and }BY = \arctan \frac{BY}{BX}
\text{diffusion vector angle between }BX\text{ and }BZ = \arctan \frac{BZ}{BX}
\text{diffusion vector angle between }BY\text{ and }BZ = \arctan \frac{BY}{BZ}

The first DTI image showing neural tracts curving through the brain in Macaca fascicularis (Filler et al 1992)

The principal application is in the imaging of white matter where the location, orientation, and anisotropy of the tracts can be measured. The architecture of the axons in parallel bundles, and their myelin sheaths, facilitate the diffusion of the water molecules preferentially along their main direction. Such preferentially oriented diffusion is called anisotropic diffusion.

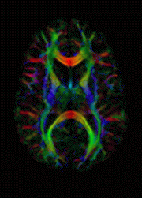
Tractographic reconstruction of neural connections via DTI

The imaging of this property is an extension of diffusion MRI. If a series of diffusion gradients (i.e. magnetic field variations in the MRI magnet) are applied that can determine at least 3 directional vectors (use of 6 different gradients is the minimum and additional gradients improve the accuracy for "off-diagonal" information), it is possible to calculate, for each voxel, a tensor (i.e. a symmetric positive definite 3 ×3 matrix) that describes the 3-dimensional shape of diffusion. The fiber direction is indicated by the tensor’s main eigenvector. This vector can be color-coded, yielding a cartography of the tracts' position and direction (red for left-right, blue for superior-inferior, and green for anterior-posterior). The brightness is weighted by the fractional anisotropy which is a scalar measure of the degree of anisotropy in a given voxel. Mean Diffusivity (MD) or Trace is a scalar measure of the total diffusion within a voxel. These measures are commonly used clinically to localize white matter lesions that do not show up on other forms of clinical MRI.

Diffusion tensor imaging data can be used to perform tractography within white matter. Fiber tracking algorithms can be used to track a fiber along its whole length (e.g. the corticospinal tract, through which the motor information transit from the motor cortex to the spinal cord and the peripheral nerves). Tractography is a useful tool for measuring deficits in white matter, such as in aging. Its estimation of fiber orientation and strength is increasingly accurate, and it has widespread potential implications in the fields of cognitive neuroscience and neurobiology.

Some clinical applications of DTI are in the tract-specific localization of white matter lesions such as trauma and in defining the severity of diffuse traumatic brain injury. The localization of tumors in relation to the white matter tracts (infiltration, deflection), has been one the most important initial applications. In surgical planning for some types of brain tumors, surgery is aided by knowing the proximity and relative position of the corticospinal tract and a tumor.

The use of DTI for the assessment of white matter in development, pathology and degeneration has been the focus of over 2,500 research publications since 2005. It promises to be very helpful in distinguishing Alzheimer's disease from other types of dementia. Applications in brain research cover e.g. connectionistic investigation of neural networks in vivo.[5]

DTI also has applications in the characterization of skeletal and cardiac muscle. The sensitivity to fiber orientation also appears to be helpful in the arena of sports medicine where it greatly aids imaging of structure and injury in muscles and tendons.

A recent study at Barnes-Jewish Hospital and Washington University School of Medicine of healthy persons and both newly affected and chronically-afflicted individuals with optic neuritis caused by multiple sclerosis (MS) showed that DTI can be used to assess the course of the condition's effects on the eye's optic nerve and the vision because it can assess axial diffusivity of water flow in the area.

[edit] See also

[edit] Notes

  1. Filler AG, Winn HR, Howe FA, Griffith JR, Bell BA, Deacon TW. Axonal transport of superparamagnetic metal oxide particles: Potential for magnetic resonance assessments of axoplasmic flow in clinical neuroscience. In: Proceedings, Society of Magnetic Resonance in Medicine, 10th Annual Meeting, San Francisco, Book of Abstracts, 10:985 (1991).
  2. Filler AG, Tsuruda JS, Richards TL, Howe FA: Images, apparatus, algorithms and methods. Patent application no. GB9216383.1, UK Patent Office, (1992) - now U.S. Patent No. 5,560,360.
  3. Richards TL, Heide AC, Tsuruda JS, Alvord EC: Vector analysis of diffusion images in experimental allergic encephalomyelitis. Presented at Society for Magnetic Resonance in Medicine, Berlin, SMRM Proceedings 11:412, (1992).
  4. Filler AG, Tsuruda JS, Richards TL, Howe FA: Image Neurography and Diffusion Anisotropy Imaging. US 5,560,360, Unites States Patent Office, (1993).

[edit] References

  1. ^ Torrey, "Bloch Equations with Diffusion Terms", Physical Review, Vol 104, p. 563-565, 1956.
  2. ^ Filler AG, Winn HR, Howe FA, Griffith JR, Bell BA, Deacon TW. Axonal transport of superparamagnetic metal oxide particles: Potential for magnetic resonance assessments of axoplasmic flow in clinical neuroscience. In: Proceedings, Society of Magnetic Resonance in Medicine, 10th Annual Meeting, San Francisco, Book of Abstracts, 10:985 (1991).
  3. ^ Filler AG, Tsuruda JS, Richards TL, Howe FA: Images, apparatus, algorithms and methods. GB 9216383, UK Patent Office, 1992.
  4. ^ Richards TL, Heide AC, Tsuruda JS, Alvord EC: Vector analysis of diffusion images in experimental allergic encephalomyelitis. Presented at Society for Magnetic Resonance in Medicine, Berlin, SMRM Proceedings 11:412, 1992 (abstr).
  5. ^ L. Minati, D. Aquino, Probing neural connectivity through Diffusion Tensor Imaging (DTI), In: R. Trappl (Ed.) Cybernetics and Systems 2006:263-68, 2006

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Diffusion_MRI#Diffusion_tensor_imaging"
Personal tools