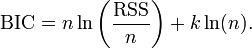Bayesian information criterion
From Wikipedia, the free encyclopedia
In statistics, the Bayesian information criterion (BIC) or Schwarz Criterion (also SBC, SBIC) is a criterion for model selection among a class of parametric models with different numbers of parameters. Choosing a model to optimize BIC is a form of regularization.
When estimating model parameters using maximum likelihood estimation, it is possible to increase the likelihood by adding additional parameters, which may result in overfitting. The BIC resolves this problem by introducing a penalty term for the number of parameters in the model. This penalty for additional parameters is stronger than that of the AIC.
The BIC was developed by Gideon E. Schwarz, who gave a Bayesian argument for adopting it.[1] It is very closely related to the Akaike information criterion.
Contents |
[edit] Mathematically
The BIC is an asymptotic result derived under the assumptions that the data distribution is in the exponential family. Let:
- x = the observed data;
- n = the number of data points in x, the number of observations, or equivalently, the sample size;
- k = the number of free parameters to be estimated. If the estimated model is a linear regression, k is the number of regressors, including the constant;
- p(x|k) = the likelihood of the observed data given the number of parameters;
- L = the maximized value of the likelihood function for the estimated model.
The formula for the BIC is[2]:
Under the assumption that the model errors or disturbances are normally distributed, this becomes (up to an additive constant, which depends only on n and not on the model):
where RSS is the residual sum of squares from the estimated model. Note that the term for 
used in this specialization is equal to the rescaled normal loglikelihood up to an additive constant that depends only on n
Given any two estimated models, the model with the lower value of BIC is the one to be preferred. The BIC is an increasing function of RSS and an increasing function of k. That is, unexplained variation in the dependent variable and the number of explanatory variables increase the value of BIC. Hence, lower BIC implies either fewer explanatory variables, better fit, or both. The BIC penalizes free parameters more strongly than does the Akaike information criterion.
It is important to keep in mind that the BIC can be used to compare estimated models only when the numerical values of the dependent variable are identical for all estimates being compared. The models being compared need not be nested, unlike the case when models are being compared using an F or likelihood ratio test.
[edit] Characteristics of the Bayesian information criterion
- It is independent of the prior.
- It can measure the efficiency of the parameterized model in terms of predicting the data.
- It penalizes the complexity of the model where complexity refers to the number of parameters in model.
- It is exactly equal to the minimum description length criterion but with negative sign.
- It can be used to choose the number of clusters according to the intrinsic complexity present in a particular dataset.
- It is closely related to other penalized likelihood criteria such as RIC and the Akaike information criterion.
[edit] Applications
BIC has been widely used for model identification in time series and linear regression. It can, however, be applied quite widely to any set of maximum likelihood-based models. However, it should be noted that in many applications (for example, selecting a black body or power law spectrum for an astronomical source), BIC simply reduces to maximum likelihood selection because the number of parameters is equal for the models of interest.
[edit] Notes
[edit] References
- Liddle, A.R., "Information criteria for astrophysical model selection", http://xxx.adelaide.edu.au/PS_cache/astro-ph/pdf/0701/0701113v2.pdf
- McQuarrie, A. D. R., and Tsai, C.-L., 1998. Regression and Time Series Model Selection. World Scientific.
[edit] See also
- Akaike information criterion
- Bayesian model comparison
- Deviance information criterion
- Jensen-Shannon divergence
- Kullback-Leibler divergence
- Model selection
