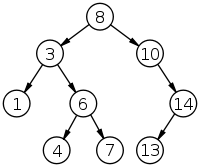
Binary search tree
From Wikipedia, the free encyclopedia
In computer science, a binary search tree (BST) is a binary tree data structure which has the following properties:
- Each node (item in the tree) has a distinct value.
- Both the left and right subtrees must also be binary search trees.
- The left subtree of a node contains only values less than the node's value.
- The right subtree of a node contains only values greater than the node's value.
The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient.
Binary search trees can choose to allow or disallow duplicate values, depending on the implementation.
Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays.
Contents |
[edit] Operations
Operations on a binary tree require comparisons between nodes. These comparisons are made with calls to a comparator, which is a subroutine that computes the total order (linear order) on any two values. This comparator can be explicitly or implicitly defined, depending on the language in which the BST is implemented.
[edit] Searching
Searching a binary tree for a specific value can be a recursive or iterative process. This explanation covers a recursive method.
We begin by examining the root node. If the tree is null, the value we are searching for does not exist in the tree. Otherwise, if the value equals the root, the search is successful. If the value is less than the root, search the left subtree. Similarly, if it is greater than the root, search the right subtree. This process is repeated until the value is found or the indicated subtree is null. If the searched value is not found before a null subtree is reached, then the item must not be present in the tree.
Here is the search algorithm in the Python programming language:
def search_binary_tree(node, key): if node is None: return None # key not found if key < node.key: return search_binary_tree(node.left, key) elif key > node.key: return search_binary_tree(node.right, key) else: # key is equal to node key return node.value # found key
This operation requires O(log n) time in the average case, but needs O(n) time in the worst-case, when the unbalanced tree resembles a linked list (degenerate tree).
[edit] Insertion
Insertion begins as a search would begin; if the root is not equal to the value, we search the left or right subtrees as before. Eventually, we will reach an external node and add the value as its right or left child, depending on the node's value. In other words, we examine the root and recursively insert the new node to the left subtree if the new value is less than the root, or the right subtree if the new value is greater than or equal to the root.
Here's how a typical binary search tree insertion might be performed in C++:
/* Inserts the node pointed to by "newNode" into the subtree rooted at "treeNode" */ void InsertNode(Node* &treeNode, Node *newNode) { if (treeNode == NULL) treeNode = newNode; else if (newNode->key < treeNode->key) InsertNode(treeNode->left, newNode); else InsertNode(treeNode->right, newNode); }
The above "destructive" procedural variant modifies the tree in place. It uses only constant space, but the previous version of the tree is lost. Alternatively, as in the following Python example, we can reconstruct all ancestors of the inserted node; any reference to the original tree root remains valid, making the tree a persistent data structure:
def binary_tree_insert(node, key, value): if node is None: return TreeNode(None, key, value, None) if key == node.key: return TreeNode(node.left, key, value, node.right) if key < node.key: return TreeNode(binary_tree_insert(node.left, key, value), node.key, node.value, node.right) else: return TreeNode(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))
The part that is rebuilt uses Θ(log n) space in the average case and Ω(n) in the worst case (see big-O notation).
In either version, this operation requires time proportional to the height of the tree in the worst case, which is O(log n) time in the average case over all trees, but Ω(n) time in the worst case.
Another way to explain insertion is that in order to insert a new node in the tree, its value is first compared with the value of the root. If its value is less than the root's, it is then compared with the value of the root's left child. If its value is greater, it is compared with the root's right child. This process continues, until the new node is compared with a leaf node, and then it is added as this node's right or left child, depending on its value.
There are other ways of inserting nodes into a binary tree, but this is the only way of inserting nodes at the leaves and at the same time preserving the BST structure.
[edit] Deletion
There are several cases to be considered:
- Deleting a leaf: Deleting a node with no children is easy, as we can simply remove it from the tree.
- Deleting a node with one child: Delete it and replace it with its child.
- Deleting a node with two children: Suppose the node to be deleted is called N. We replace the value of N with either its in-order successor (the left-most child of the right subtree) or the in-order predecessor (the right-most child of the left subtree).
Once we find either the in-order successor or predecessor, swap it with N, and then delete it. Since both the successor and the predecessor must have fewer than two children, either one can be deleted using the previous two cases. A good implementation avoids consistently using one of these nodes, however, because this can unbalance the tree.
Here is C sample code for a recursive version of deletion.
struct Binary_Search_Tree *Bst_Delete(struct Binary_Search_Tree *node, int val) { struct Binary_Search_Tree *successor, *node_delete; if(node) { if(node->val > val) node->left = Bst_Delete(node->left, val); else if(node->val < val) node->right = Bst_Delete(node->right, val); else { if(node->left == NULL) { node_delete = node; node = node->right; free(node_delete); } else if(node->right == NULL) { node_delete = node; node = node->left; free(node_delete); } else /* use inorder_predecessor every alternate delete for better tree balancing */ { successor = inorder_successor_Bst(node->right); node->val = successor->val; node->right = Bst_Delete(node->right, successor->val); } } return node; } else { printf("\nNode to be deleted not found\n"); return NULL; } }
Although this operation does not always traverse the tree down to a leaf, this is always a possibility; thus in the worst case it requires time proportional to the height of the tree. It does not require more even when the node has two children, since it still follows a single path and does not visit any node twice.
Here is the code in Python:
def findSuccessor(self): succ = None if self.rightChild: succ = self.rightChild.findMin() else: if self.parent.leftChild == self: succ = self.parent else: self.parent.rightChild = None succ = self.parent.findSuccessor() self.parent.rightChild = self return succ def findMin(self): n = self while n.leftChild: n = n.leftChild print 'found min, key = ', n.key return n def spliceOut(self): if (not self.leftChild and not self.rightChild): if self == self.parent.leftChild: self.parent.leftChild = None else: self.parent.rightChild = None elif (self.leftChild or self.rightChild): if self.leftChild: if self == self.parent.leftChild: self.parent.leftChild = self.leftChild else: self.parent.rightChild = self.leftChild else: if self == self.parent.leftChild: self.parent.leftChild = self.rightChild else: self.parent.rightChild = self.rightChild def binary_tree_delete(self, key): if self.key == key: if not (self.leftChild or self.rightChild): if self == self.parent.leftChild: self.parent.leftChild = None else: self.parent.rightChild = None elif (self.leftChild or self.rightChild) and (not (self.leftChild and self.rightChild)): if self.leftChild: if self == self.parent.leftChild: self.parent.leftChild = self.leftChild else: self.parent.rightChild = self.leftChild else: if self == self.parent.leftChild: self.parent.leftChild = self.rightChild else: self.parent.rightChild = self.rightchild else: succ = self.findSuccessor() succ.spliceOut() if self == self.parent.leftChild: self.parent.leftChild = succ else: self.parent.rightChild = succ succ.leftChild = self.leftChild succ.rightChild = self.rightChild else: if key < self.key:
[edit] Traversal
Once the binary search tree has been created, its elements can be retrieved in-order by recursively traversing the left subtree of the root node, accessing the node itself, then recursively traversing the right subtree of the node, continuing this pattern with each node in the tree as it's recursively accessed. The tree may also be traversed in pre-order or post-order traversals.
def traverse_binary_tree(treenode): if treenode is None: return left, nodevalue, right = treenode traverse_binary_tree(left) visit(nodevalue) traverse_binary_tree(right)
Traversal requires Ω(n) time, since it must visit every node. This algorithm is also O(n), and so it is asymptotically optimal.
[edit] Sort
A binary search tree can be used to implement a simple but efficient sorting algorithm. Similar to heapsort, we insert all the values we wish to sort into a new ordered data structure—in this case a binary search tree—and then traverse it in order, building our result:
def build_binary_tree(values): tree = None for v in values: tree = binary_tree_insert(tree, v) return tree def traverse_binary_tree(treenode): if treenode is None: return [] else: left, value, right = treenode return (traverse_binary_tree(left), [value], traverse_binary_tree(right))
The worst-case time of build_binary_tree is Θ(n2)—if you feed it a sorted list of values, it chains them into a linked list with no left subtrees. For example, build_binary_tree([1, 2, 3, 4, 5]) yields the tree (None, 1, (None, 2, (None, 3, (None, 4, (None, 5, None))))).
There are several schemes for overcoming this flaw with simple binary trees; the most common is the self-balancing binary search tree. If this same procedure is done using such a tree, the overall worst-case time is O(nlog n), which is asymptotically optimal for a comparison sort. In practice, the poor cache performance and added overhead in time and space for a tree-based sort (particularly for node allocation) make it inferior to other asymptotically optimal sorts such as heapsort for static list sorting. On the other hand, it is one of the most efficient methods of incremental sorting, adding items to a list over time while keeping the list sorted at all times...
[edit] Example for a Binary Search Tree in Python:
class Node: def __init__(self, lchild=None, rchild=None, value=-1, data=None): self.lchild = lchild self.rchild = rchild self.value = value self.data = data class Bst: """Implement Binary Search Tree.""" def __init__(self): self.l = [] # Nodes self.root = None def add(self, key, dt): """Add a node in tree.""" if self.root == None: self.root = Node(value=key, data=dt) self.l.append(self.root) return 0 else: self.p = self.root while True: if self.p.value > key: if self.p.lchild == None: self.p.lchild = Node(value=key, data=dt) return 0 # Success else: self.p = self.p.lchild elif self.p.value == key: return -1 # Value already in tree else: if self.p.rchild == None: self.p.rchild = Node(value=key, data=dt) return 0 # Success else: self.p = self.p.rchild return -2 # Should never happen def search(self, key): """Search Tree for a key and return data; if not found return None.""" self.p = self.root if self.p == None: return None while True: # print self.p.value, self.p.data if self.p.value > key: if self.p.lchild == None: return None # Not found else: self.p = self.p.lchild elif self.p.value == key: return self.p.data else: if self.p.rchild == None: return None # Not found else: self.p = self.p.rchild return None # Should never happen def deleteNode(self, key): """Delete node with value == key.""" if self.root.value == key: if self.root.rchild == None: if self.root.lchild == None: self.root = None else: self.root = self.root.lchild else: self.root.rchild.lchild = self.root.lchild self.root = self.root.rchild return 1 self.p = self.root while True: if self.p.value > key: if self.p.lchild == None: return 0 # Not found anything to delete elif self.p.lchild.value == key: self.p.lchild = self.proceed(self.p, self.p.lchild) return 1 else: self.p = self.p.lchild # There's no way for self.p.value to be equal to key: if self.p.value < key: if self.p.rchild == None: return 0 # Not found anything to delete elif self.p.rchild.value == key: self.p.rchild = self.proceed(self.p, self.p.rchild) return 1 else: self.p = self.p.rchild return 0 def proceed(self, parent, delValue): if delValue.lchild == None and delValue.rchild == None: return None elif delValue.rchild == None: return delValue.lchild else: return delValue.rchild def sort(self): self.__traverse__(self.root, mode=1) def __traverse__(self, v, mode=0): """Traverse in: preorder = 0, inorder = 1, postorder = 2.""" if v == None: return if mode == 0: print (v.value, v.data) self.__traverse__(v.lchild) self.__traverse__(v.rchild) elif mode == 1: self.__traverse__(v.lchild, 1) print (v.value, v.data) self.__traverse__(v.rchild, 1) else: self.__traverse__(v.lchild, 2) self.__traverse__(v.rchild, 2) print (v.value, v.data) def main(): tree = Bst() tree.add(4, "test1") tree.add(10, "test2") tree.add(23, "test3") tree.add(1, "test4") tree.add(3, "test5") tree.add(2, "test6") tree.sort() print tree.search(3) print tree.deleteNode(10) print tree.deleteNode(23) print tree.deleteNode(4) print tree.search(3) tree.sort() if __name__ == "__main__": main()
[edit] Types of binary search trees
There are many types of binary search trees. AVL trees and red-black trees are both forms of self-balancing binary search trees. A splay tree is a binary search tree that automatically moves frequently accessed elements nearer to the root. In a treap ("tree heap"), each node also holds a priority and the parent node has higher priority than its children.
Two other titles describing binary search trees are that of a complete and degenerate tree.
A complete tree is a tree with n levels, where for each level d <= n - 1, the number of existing nodes at level d is equal to 2d. This means all possible nodes exist at these levels. An additional requirement for a complete binary tree is that for the nth level, while every node does not have to exist, the nodes that do exist must fill from left to right.
A degenerate tree is a tree where for each parent node, there is only one associated child node. What this means is that in a performance measurement, the tree will essentially behave like a linked list data structure.
[edit] Performance comparisons
D. A. Heger (2004)[1] presented a performance comparison of binary search trees. Treap was found to have the best average performance, while red-black tree was found to have the smallest amount of performance fluctuations.
[edit] Optimal binary search trees
If we don't plan on modifying a search tree, and we know exactly how often each item will be accessed, we can construct an optimal binary search tree, which is a search tree where the average cost of looking up an item (the expected search cost) is minimized.
Assume that we know the elements and that for each element, we know the proportion of future lookups which will be looking for that element. We can then use a dynamic programming solution, detailed in section 15.5 of Introduction to Algorithms (Second Edition) by Thomas H. Cormen, to construct the tree with the least possible expected search cost.
Even if we only have estimates of the search costs, such a system can considerably speed up lookups on average. For example, if you have a BST of English words used in a spell checker, you might balance the tree based on word frequency in text corpora, placing words like "the" near the root and words like "agerasia" near the leaves. Such a tree might be compared with Huffman trees, which similarly seek to place frequently-used items near the root in order to produce a dense information encoding; however, Huffman trees only store data elements in leaves and these elements need not be ordered.
If we do not know the sequence in which the elements in the tree will be accessed in advance, we can use splay trees which are asymptotically as good as any static search tree we can construct for any particular sequence of lookup operations.
Alphabetic trees are Huffman trees with the additional constraint on order, or, equivalently, search trees with the modification that all elements are stored in the leaves. Faster algorithms exist for optimal alphabetic binary trees (OABTs).
Example:
procedure Optimum Search Tree(f, f´, c)
for j = 0 to n do
c[j, j] = 0, F[j, j] = f´j
for d = 1 to n do
for i = 0 to (n − d) do
j = i + d
F[i, j] = F[i, j − 1] + f´ + f´j
c[i, j] = MIN(i<k<=j){c[i, k − 1] + c[k, j]} + F[i, j]
[edit] See also
[edit] References
- ^ Heger, Dominique A. (2004), "A Disquisition on The Performance Behavior of Binary Search Tree Data Structures", European Journal for the Informatics Professional 5 (5), http://www.upgrade-cepis.org/issues/2004/5/up5-5Mosaic.pdf
[edit] Further reading
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Section 6.2.2: Binary Tree Searching, pp.426–458.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 12: Binary search trees, pp.253–272. Section 15.5: Optimal binary search trees, pp.356–363.
[edit] External links
- Full source code to an efficient implementation in C++
- Implementation of Binary Search Trees in C
- Implementation of Binary Search Trees in Java
- Iterative Implementation of Binary Search Trees in C#
- An introduction to binary trees from Stanford
- Dictionary of Algorithms and Data Structures - Binary Search Tree
- Binary Search Tree Example in Python
- Java Model illustrating the behaviour of binary search trees(In JAVA Applet)
- Interactive Data Structure Visualizations - Binary Tree Traversals
- Literate implementations of binary search trees in various languages on LiteratePrograms
- BST Tree Applet by Kubo Kovac
|
|||||||||||