Breadth-first search

Breadth-first search
	; Order in which the nodes are expanded
Class	Search Algorithm
Data structure	Graph
Worst case performance	O( \| V \| + \| E \| ) = O(bd)
Worst case space complexity	O( \| V \| + \| E \| ) = O(bd)
Optimal	yes (for unweighted graphs)
	This box: view • talk

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Graph search algorithms
Search A* B* Bellman-Ford algorithm Best-first search Bidirectional search Breadth-first search D* Depth-first search Depth-limited search Dijkstra's algorithm Floyd–Warshall algorithm Hill climbing Iterative deepening depth-first search Johnson's algorithm Uniform-cost search

In graph theory, breadth-first search (BFS) is a graph search algorithm that begins at the root node and explores all the neighboring nodes. Then for each of those nearest nodes, it explores their unexplored neighbor nodes, and so on, until it finds the goal.

[edit] How it works

BFS is an uninformed search method that aims to expand and examine all nodes of a graph or combinations of sequence by systematically searching through every solution. In other words, it exhaustively searches the entire graph or sequence without considering the goal until it finds it. It does not use a heuristic.

From the standpoint of the algorithm, all child nodes obtained by expanding a node are added to a FIFO queue. In typical implementations, nodes that have not yet been examined for their neighbors are placed in some container (such as a queue or linked list) called "open" and then once examined are placed in the container "closed".

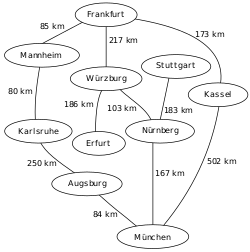
An example map of Germany with some connections between cities.

The breadth-first tree obtained when running BFS on the given map and starting in Frankfurt.

Animated example of a breadth-first search

[edit] Algorithm (informal)

Enqueue the root node.
Dequeue a node and examine it.
- If the element sought is found in this node, quit the search and return a result.
- Otherwise enqueue any successors (the direct child nodes) that have not yet been examined.
If the queue is empty, every node on the graph has been examined -- quit the search and return "not found".
Repeat from Step 2.

Note: Using a stack instead of a queue to store the nodes yet to be visited would turn this algorithm into a depth-first search.

[edit] Implementation

[edit] Python

Assume we have a graph made up of Node objects, each containing a value and a list of child Node objects:

class Node:
    """Simple structure for nodes in a graph."""
    def __init__(self, value, neighbors = None):
        if neighbors is None: neighbors = []
        self.value = value
        self.neighbors = neighbors

Then this function performs a breadth-first search on that graph whenIn graph theory, breadth-first search (BFS) is a graph search algorithm that begins at the root node and explores all the neighboring nodes. Then for each of those nearest nodes, it explores their unexplored neighbor nodes, and so on, until it finds the goal.

from collections import deque
def bfs(top_node,
        visit_function = lambda x: None,
        visited = None):
    """Breadth-first search on a graph, starting at top_node.
    Given the graph's root node (a Node instance) and a function
    to apply to each node in the graph.
    """
    if visited is None: visited = set()
    queue = deque([top_node])
    while queue:
        curr_node = queue.popleft()          # Dequeue
        if curr_node not in visited:         # Skip visited nodes
            visit_function(curr_node)        # Visit the node
            visited.add(curr_node)
            queue.extend(curr_node.neighbors) # Enqueue the neighbors

For example, this script finds the sum of the integer values of each node in the graph:

# Build an example graph
the_graph = Node(1, [Node(1, [Node(2), Node(3)]),
                     Node(5, [Node(8, [Node(13)]),
                              Node(21, [Node(34), Node(55)])])])
 
# Define a "visit" function
total = 0
def sum_graph(node):
    global total
    total += node.value
 
# Visit the whole graph
bfs(the_graph, sum_graph)
print total

[edit] C

Algorithm of Breadth-first search：

 void BFS(VLink G[], int v) { 
   int w;
   VISIT(v);                    /*visit vertex v*/
   visited[v] = 1;              /*mark v as visited : 1 */
   ADDQ(Q,v);
   while(!EMPTYQ(Q)) { 
     v = DELQ(Q);               /*Dequeue v*/
     w = FIRSTADJ(G,v);         /*Find first neighbor, return -1 if no neighbor*/
     while(w != -1) { 
       if(visited[w] == 0) { 
         VISIT(w);              /*visit vertex w*/
         ADDQ(Q,w);             /*Enqueue current visited vertex w*/
         visited[w] = 1;        /*mark w as visited*/
       }
       w = NEXTADJ(G,v);        /*Find next neighbor, return -1 if no neighbor*/
     }
   }  
 }

Main Algorithm of apply Breadth-first search to graph G=(V,E)：

 void TRAVEL_BFS(VLink G[], int visited[], int n) { 
   int i;
   for(i = 0; i < n; i ++) {
     visited[i] = 0;            /* Mark initial value as 0 */
   }
   for(i = 0; i < n; i ++)
     if(visited[i] == 0)
       BFS(G,i);
 }

[edit] C++

This is the implementation of the above informal algorithm, where the "so-far-unexamined" is handled by the parent array. For actual C++ applications, see the Boost Graph Library.

Suppose we have a struct:

struct Vertex {
 	/* Some code */
 	std::vector<int> out;
 	/* Some more code */
 };

and an array of vertices: (the algorithm will use the indices of this array, to handle the vertices)

std::vector<Vertex> graph(vertices);

the algorithm starts from start and returns true if there is a directed path from start to end:

 bool BFS(const std::vector<Vertex>& graph, int start, int end) {
   std::queue<int> next;
   std::vector<int> parent(graph.size(), -1) ;
   next.push(start);
   parent[start] = start;
   while (!next.empty()) {
     int u = next.front();
     next.pop();
     // Here is the point where you can examine the u th vertex of graph
     // For example:
     if (u == end) return true;
     for (std::vector<int>::const_iterator j = graph[u].out.begin(); j != graph[u].out.end(); ++j) {
       // Look through neighbors.
       int v = *j;
       if (parent[v] == -1) {
         // If v is unvisited.
         parent[v] = u;
         next.push(v);
       }
     }
   }
   return false;
 }

it also stores the parents of each node, from which you can get the path.

[edit] C# and Java

class Node {
 
	Node[] Children;
 
}
 
/// <summary>Prints out all the children of graph fragment <paramref name="n" /> to Console in breadth-first order</summary>
public static void BreadthFirstSearch(Node n) {
 
	// 'Queue' can be any Queue-like structure that implements Enqueue, Dequeue, and exposes a Count (Length) property
	Queue q = new Queue();
	q.Enqueue( n );
 
	while( q.Count > 0 ) {
		Node m = q.Dequeue();
 
		// Perform task on m here. For example, printing it out to the console:
		Console.WriteLine( m + ", " );
 
		foreach(Node child in m.Children) {
			q.Enqueue( child );
		}
	}
 
}

[edit] Features

Graph search algorithms
Search A* B* Bellman-Ford algorithm Best-first search Bidirectional search Breadth-first search D* Depth-first search Depth-limited search Dijkstra's algorithm Floyd–Warshall algorithm Hill climbing Iterative deepening depth-first search Johnson's algorithm Uniform-cost search

[edit] Space Complexity

Since all of the nodes of a level must be saved until their child nodes in the next level have been generated, the space complexity is proportional to the number of nodes at the deepest level. Given a branching factor $b$ and graph depth $d$ the asymptotic space complexity is the number of nodes at the deepest level, $O (b d)$ . When the number of vertices and edges in the graph are known ahead of time, the space complexity can also be expressed as $O ( | E | + | V | )$ where $| E |$ is the cardinality of the set of edges (the number of edges), and $| V |$ is the cardinality of the set of vertices. In the worst case the graph has a depth of 1 and all vertices must be stored. Since it is exponential in the depth of the graph, breadth-first search is often impractical for large problems on systems with bounded space.

[edit] Time Complexity

Since in the worst case breadth-first search has to consider all paths to all possible nodes the time complexity of breadth-first search is $b + b 2 + b 3 + ... + b d$ which asymptotically approaches $O (b d)$ . The time complexity can also be expressed as $O ( | E | + | V | )$ since every vertex and every edge will be explored in the worst case.

[edit] Completeness

Breadth-first search is complete. This means that if there is a solution breadth-first search will find it regardless of the kind of graph. However, if the graph is infinite and there is no solution breadth-first search will diverge.

[edit] Optimality

For unit-step cost, breadth-first search is optimal. In general breadth-first search is not optimal since it always returns the result with the fewest edges between the start node and the goal node. If the graph is a weighted graph, and therefore has costs associated with each step, a goal next to the start does not have to be the cheapest goal available. This problem is solved by improving breadth-first search to uniform-cost search which considers the path costs. Nevertheless, if the graph is not weighted, and therefore all step costs are equal, breadth-first search will find the nearest and the best solution.

[edit] Applications of BFS

Breadth-first search can be used to solve many problems in graph theory, for example:

Finding all connected components in a graph.
Finding all nodes within one connected component
Copying Collection, Cheney's algorithm
Finding the shortest path between two nodes u and v (in an unweighted graph)
Finding the shortest path between two nodes u and v (in a weighted graph: see talk page)
Testing a graph for bipartiteness
(Reverse) Cuthill–McKee mesh numbering

[edit] Finding connected Components

The set of nodes reached by a BFS (breadth-first search) form the largest connected component containing the starting node.

[edit] Testing bipartiteness

BFS can be used to test bipartiteness, by starting the search at any vertex and giving alternating labels to the vertices visited during the search. That is, give label 0 to the starting vertex, 1 to all its neighbours, 0 to those neighbours' neighbours, and so on. If at any step a vertex has (visited) neighbours with the same label as itself, then the graph is not bipartite. If the search ends without such a situation occurring, then the graph is bipartite.

[edit] Literature

Knuth, Donald E. (1997), The Art Of Computer Programming Vol 1. 3rd ed., Boston: Addison-Wesley, ISBN 0-201-89683-4, http://www-cs-faculty.stanford.edu/~knuth/taocp.html

[edit] External links

Breadth-First shortest-route search implemented in T-SQL by Martin Withaar