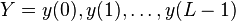Hidden Markov model

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Probabilistic parameters of a hidden Markov model (example)
x — states
y — possible observations
a — state transition probabilities
b — output probabilities

A hidden Markov model (HMM) is a statistical model in which the system being modeled is assumed to be a Markov process with unobserved state. An HMM can be considered as the simplest dynamic Bayesian network.

In a regular Markov model, the state is directly visible to the observer, and therefore the state transition probabilities are the only parameters. In a hidden Markov model, the state is not directly visible, but output dependent on the state is visible. Each state has a probability distribution over the possible output tokens. Therefore the sequence of tokens generated by an HMM gives some information about the sequence of states. Note that the adjective 'hidden' refers to the state sequence through which the model passes, not to the parameters of the model; Even if the model parameters are known exactly, the model is still 'hidden'.

Hidden Markov models are especially known for their application in temporal pattern recognition such as speech, handwriting, gesture recognition, part-of-speech tagging, musical score following, partial discharges and bioinformatics.

Contents

[edit] Architecture of a hidden Markov model

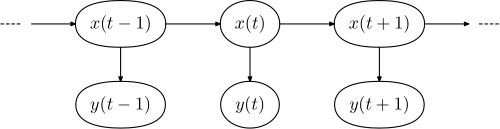
The diagram below shows the general architecture of an instantiated HMM. Each oval shape represents a random variable that can adopt any of a number of values. The random variable x(t) is the hidden state at time t (with the model from the above diagram, x(t) ∈ { x1, x2, x3 }). The random variable y(t) is the observation at time t (y(t) ∈ { y1, y2, y3, y4 }). The arrows in the diagram (often called a trellis diagram) denote conditional dependencies.

From the diagram, it is clear that the conditional probability distribution of the hidden variable x(t) at time t, given the value of the hidden variable x(t − 1), depends only on the value of the hidden variable x(t − 1): the values at time t − 2 and before have no influence. This is called the Markov property. Similarly, the value of the observed variable y(t) only depends on the value of the hidden variable x(t) (both at time t).

Temporal evolution of a hidden Markov model

[edit] Probability of an observed sequence

The observation sequence above can be produced by the following state sequences.
5 3 2 5 3 2
5 3 1 2 1 2
4 3 2 5 3 2
4 3 1 2 1 2
3 1 2 5 3 2
Transition and observation probabilities are indicated by the line opacity.

The probability of observing a sequence

Y=y(0), y(1),\dots,y(L-1)\,

of length L is given by

P(Y)=\sum_{X}P(Y\mid X)P(X),\,

where the sum runs over all possible hidden-node sequences

X=x(0), x(1), \dots, x(L-1).\,

Brute-force calculation of P(Y) is intractable for most real-life problems, as the number of possible hidden node sequences is typically extremely high and scales exponentially with the length of the sequence. The calculation can however be sped up enormously using the forward algorithm [1] or the equivalent backward algorithm.

[edit] Using hidden Markov models

There are three canonical problems associated with HMM

  • Given the parameters of the model, compute the probability of a particular output sequence. This requires summation over all possible state sequences, but can be done efficiently using the forward algorithm, which is a form of dynamic programming.
  • Given the parameters of the model and a particular output sequence, find the state sequence that is most likely to have generated that output sequence. This requires finding a maximum over all possible state sequences, but can similarly be solved efficiently by the Viterbi algorithm.
  • Given an output sequence or a set of such sequences, find the most likely set of state transition and output probabilities. In other words, derive the maximum likelihood estimate of the parameters of the HMM given a dataset of output sequences. No tractable algorithm is known for solving this problem exactly, but a local maximum likelihood can be derived efficiently using the Baum-Welch algorithm or the Baldi-Chauvin algorithm. The Baum-Welch algorithm is also known as the forward-backward algorithm, and is a special case of the Expectation-maximization algorithm.

[edit] A concrete example

Consider two friends, Alice and Bob, who live far apart from each other and who talk together daily over the telephone about what they did that day. Bob is only interested in three activities: walking in the park, shopping, and cleaning his apartment. The choice of what to do is determined exclusively by the weather on a given day. Alice has no definite information about the weather where Bob lives, but she knows general trends. Based on what Bob tells her he did each day, Alice tries to guess what the weather must have been like.

Alice believes that the weather operates as a discrete Markov chain. There are two states, "Rainy" and "Sunny", but she cannot observe them directly, that is, they are hidden from her. On each day, there is a certain chance that Bob will perform one of the following activities, depending on the weather: "walk", "shop", or "clean". Since Bob tells Alice about his activities, those are the observations. The entire system is that of a hidden Markov model (HMM).

Alice knows the general weather trends in the area, and what Bob likes to do on average. In other words, the parameters of the HMM are known. They can be written down in the Python programming language:

states = ('Rainy', 'Sunny')
 
observations = ('walk', 'shop', 'clean')
 
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
 
transition_probability = {
   'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
   'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
   }
 
emission_probability = {
   'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
   'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
   }

In this piece of code, start_probability represents Alice's belief about which state the HMM is in when Bob first calls her (all she knows is that it tends to be rainy on average). The particular probability distribution used here is not the equilibrium one, which is (given the transition probabilities) actually approximately {'Rainy': 0.571, 'Sunny': 0.429}. The transition_probability represents the change of the weather in the underlying Markov chain. In this example, there is only a 30% chance that tomorrow will be sunny if today is rainy. The emission_probability represents how likely Bob is to perform a certain activity on each day. If it is rainy, there is a 50% chance that he is cleaning his apartment; if it is sunny, there is a 60% chance that he is outside for a walk.

Graphical representation of the given HMM

This example is further elaborated in the Viterbi algorithm page.

[edit] Applications of hidden Markov models

[edit] History

Hidden Markov Models were first described in a series of statistical papers by Leonard E. Baum and other authors in the second half of the 1960s. One of the first applications of HMMs was speech recognition, starting in the mid-1970s.[2]

In the second half of the 1980s, HMMs began to be applied to the analysis of biological sequences, in particular DNA. Since then, they have become ubiquitous in the field of bioinformatics.[3]

[edit] See also

[edit] Notes

  1. ^ Rabiner, p. 262
  2. ^ Rabiner, p. 258
  3. ^ Durbin et al.

[edit] References

The path-counting algorithm, an alternative to the Baum-Welch algorithm:

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Hidden_Markov_model"
Personal tools