,first 7thgrade amazing! apple astronomer astronomy bibliotextual_studies bio.wiki biographie biography blogging calculus england gravity history historyofmath info isaac liberalarts math newton people philosophy physics read science system

My tags:

From Wikipedia, the free encyclopedia

Sir Isaac Newton
Godfrey Kneller's 1689 portrait of Isaac Newton (aged 46)
Born	4 January 1643(1643-01-04) [OS: 25 December 1642][1] Woolsthorpe-by-Colsterworth Lincolnshire, England
Died	31 March 1727 (aged 84) [OS: 20 March 1726][1] Kensington, Middlesex, England
Residence	England
Citizenship	English
Nationality	English (British from 1707)
Fields	Physics, mathematics, astronomy, natural philosophy, alchemy, theology
Institutions	University of Cambridge Royal Society Royal Mint
Alma mater	Trinity College, Cambridge
Academic advisors	Isaac Barrow[2] Benjamin Pulleyn[3][4]
Notable students	Roger Cotes William Whiston
Known for	Newtonian mechanics Universal gravitation Calculus Optics
Influences	Henry More
Influenced	Nicolas Fatio de Duillier John Keill
Religious stance	Arianism; for details see article
Signature
Notes His mother was Hannah Ayscough. His half-niece was Catherine Barton.

Sir Isaac Newton, FRS (4 January 1643  – 31 March 1727 [OS: 25 December 1642 – 20 March 1727])^[1] was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian and one of the most influential men in human history. His Philosophiæ Naturalis Principia Mathematica, published in 1687, is considered to be the most influential book in the history of science, laying the groundwork for most of classical mechanics. In this work, Newton described universal gravitation and the three laws of motion which dominated the scientific view of the physical universe for the next three centuries. Newton showed that the motions of objects on Earth and of celestial bodies are governed by the same set of natural laws by demonstrating the consistency between Kepler's laws of planetary motion and his theory of gravitation, thus removing the last doubts about heliocentrism and advancing the scientific revolution.

In mechanics, Newton enunciated the principles of conservation of both momentum and angular momentum. In optics, he built the first practical reflecting telescope^[5] and developed a theory of colour based on the observation that a prism decomposes white light into the many colours which form the visible spectrum. He also formulated an empirical law of cooling and studied the speed of sound.

In mathematics, Newton shares the credit with Gottfried Leibniz for the development of the differential and integral calculus. He also demonstrated the generalised binomial theorem, developed the so-called "Newton's method" for approximating the zeroes of a function, and contributed to the study of power series.

Newton's stature among scientists remains at the very top rank, as demonstrated by a 2005 survey of scientists in Britain's Royal Society asking who had the greater effect on the history of science, Newton or Albert Einstein. Newton was deemed the more influential.^[6]

Newton was also highly religious (though unorthodox), producing more work on Biblical hermeneutics than the natural science he is remembered for today.

Contents 1 Life 1.1 Early years 1.2 Middle years 1.2.1 Mathematics 1.2.2 Optics 1.2.3 Mechanics and gravitation 1.3 Later life 1.4 After death 1.4.1 Fame 1.4.2 Commemorations 1.5 Newton in popular culture 2 Religious views 2.1 Effect on religious thought 2.2 Views of the end of the world 3 Enlightenment philosophers 4 Newton and the counterfeiters 5 Newton's laws of motion 6 Newton's apple 7 Writings by Newton 8 See also 9 Footnotes and references 10 References 11 Further reading 11.1 Newton and religion 11.2 Primary sources 12 External links

Life

Early years

Isaac Newton was born on 4 January 1643 [OS: 25 December 1642]^[1] at Woolsthorpe Manor in Woolsthorpe-by-Colsterworth, a hamlet in the county of Lincolnshire. At the time of Newton's birth, England had not adopted the latest papal calendar and therefore his date of birth was recorded as Christmas Day, 25 December 1642. Newton was born three months after the death of his father. Born prematurely, he was a small child; his mother Hannah Ayscough reportedly said that he could have fit inside a quart mug. When Newton was three, his mother remarried and went to live with her new husband, the Reverend Barnabus Smith, leaving her son in the care of his maternal grandmother, Margery Ayscough. The young Isaac disliked his stepfather and held some enmity towards his mother for marrying him, as revealed by this entry in a list of sins committed up to the age of 19: "Threatening my father and mother Smith to burn them and the house over them."^[7]

From the age of about twelve until he was seventeen, Newton was educated at The King's School, Grantham (where his signature can still be seen upon a library window sill). He was removed from school, and by October 1659, he was to be found at Woolsthorpe-by-Colsterworth, where his mother, widowed by now for a second time, attempted to make a farmer of him. He hated farming. Henry Stokes, master at the King's School, persuaded his mother to send him back to school so that he might complete his education. Motivated partly by a desire for revenge against a schoolyard bully, he became the top-ranked student.^[8]

In June 1661, he was admitted to Trinity College, Cambridge as a sizar--a sort of work-study role.^[9] At that time, the college's teachings were based on those of Aristotle, but Newton preferred to read the more advanced ideas of modern philosophers such as Descartes and astronomers such as Copernicus, Galileo, and Kepler. In 1665, he discovered the generalized binomial theorem and began to develop a mathematical theory that would later become infinitesimal calculus. Soon after Newton had obtained his degree in August of 1665, the University closed down as a precaution against the Great Plague. Although he had been undistinguished as a Cambridge student,^[10] Newton's private studies at his home in Woolsthorpe over the subsequent two years saw the development of his theories on calculus, optics and the law of gravitation. In 1667 he returned to Cambridge as a fellow of Trinity.^[11]

Middle years

Mathematics

Most modern historians believe that Newton and Leibniz developed infinitesimal calculus independently, using their own unique notations. According to Newton's inner circle, Newton had worked out his method years before Leibniz, yet he published almost nothing about it until 1693, and did not give a full account until 1704. Meanwhile, Leibniz began publishing a full account of his methods in 1684. Moreover, Leibniz's notation and "differential Method" were universally adopted on the Continent, and after 1820 or so, in the British Empire. Whereas Leibniz's notebooks show the advancement of the ideas from early stages until maturity, there is only the end product in Newton's known notes. Newton claimed that he had been reluctant to publish his calculus because he feared being mocked for it. Newton had a very close relationship with Swiss mathematician Nicolas Fatio de Duillier, who from the beginning was impressed by Newton's gravitational theory. In 1691 Duillier planned to prepare a new version of Newton's Philosophiae Naturalis Principia Mathematica, but never finished it. However, in 1693 the relationship between the two men changed. At the time, Duillier had also exchanged several letters with Leibniz.^[12]

Starting in 1699, other members of the Royal Society (of which Newton was a member) accused Leibniz of plagiarism, and the dispute broke out in full force in 1711. Newton's Royal Society proclaimed in a study that it was Newton who was the true discoverer and labeled Leibniz a fraud. This study was cast into doubt when it was later found that Newton himself wrote the study's concluding remarks on Leibniz. Thus began the bitter Newton v. Leibniz calculus controversy, which marred the lives of both Newton and Leibniz until the latter's death in 1716.^[13]

Newton is generally credited with the generalized binomial theorem, valid for any exponent. He discovered Newton's identities, Newton's method, classified cubic plane curves (polynomials of degree three in two variables), made substantial contributions to the theory of finite differences, and was the first to use fractional indices and to employ coordinate geometry to derive solutions to Diophantine equations. He approximated partial sums of the harmonic series by logarithms (a precursor to Euler's summation formula), and was the first to use power series with confidence and to revert power series.

He was elected Lucasian Professor of Mathematics in 1669. In that day, any fellow of Cambridge or Oxford had to be an ordained Anglican priest. However, the terms of the Lucasian professorship required that the holder not be active in the church (presumably so as to have more time for science). Newton argued that this should exempt him from the ordination requirement, and Charles II, whose permission was needed, accepted this argument. Thus a conflict between Newton's religious views and Anglican orthodoxy was averted.^[14]

Optics

From 1670 to 1672, Newton lectured on optics. During this period he investigated the refraction of light, demonstrating that a prism could decompose white light into a spectrum of colours, and that a lens and a second prism could recompose the multicoloured spectrum into white light.^[16]

He also showed that the coloured light does not change its properties by separating out a coloured beam and shining it on various objects. Newton noted that regardless of whether it was reflected or scattered or transmitted, it stayed the same colour. Thus, he observed that colour is the result of objects interacting with already-coloured light rather than objects generating the colour themselves. This is known as Newton's theory of colour.^[17]

From this work he concluded that the lens of any refracting telescope would suffer from the dispersion of light into colours (chromatic aberration), and as a proof of the concept he constructed a telescope using a mirror as the objective to bypass that problem. ^[18] Actually building the design, the first know functional reflecting telescope, today known as a Newtonian telescope^[19], involved solving the problem of a suitable mirror material and shaping technique. Newton ground his own mirrors out of a custom composition of highly reflective speculum metal, using Newton's rings to judge the quality of the optics for his telescopes. By February of 1669 he was able to produce an instrument without chromatic aberration. In 1671 the Royal Society asked for a demonstration of his reflecting telescope.^[20] Their interest encouraged him to publish his notes On Colour, which he later expanded into his Opticks. When Robert Hooke criticised some of Newton's ideas, Newton was so offended that he withdrew from public debate. The two men remained enemies until Hooke's death.^{[citation needed]}

Newton argued that light is composed of particles or corpuscles, which were refracted by accelerating toward the denser medium, but he had to associate them with waves to explain the diffraction of light (Opticks Bk. II, Props. XII-L). Later physicists instead favoured a purely wavelike explanation of light to account for diffraction. Today's quantum mechanics, photons and the idea of wave–particle duality bear only a minor resemblance to Newton's understanding of light.

In his Hypothesis of Light of 1675, Newton posited the existence of the ether to transmit forces between particles. The contact with the theosophist Henry More, revived his interest in alchemy. He replaced the ether with occult forces based on Hermetic ideas of attraction and repulsion between particles. John Maynard Keynes, who acquired many of Newton's writings on alchemy, stated that "Newton was not the first of the age of reason: he was the last of the magicians."^[21] Newton's interest in alchemy cannot be isolated from his contributions to science.^[22] (This was at a time when there was no clear distinction between alchemy and science.) Had he not relied on the occult idea of action at a distance, across a vacuum, he might not have developed his theory of gravity. (See also Isaac Newton's occult studies.)

In 1704 Newton published Opticks, in which he expounded his corpuscular theory of light. He considered light to be made up of extremely subtle corpuscles, that ordinary matter was made of grosser corpuscles and speculated that through a kind of alchemical transmutation "Are not gross Bodies and Light convertible into one another, …and may not Bodies receive much of their Activity from the Particles of Light which enter their Composition?"^[23] Newton also constructed a primitive form of a frictional electrostatic generator, using a glass globe (Optics, 8th Query).

Mechanics and gravitation

In 1677, Newton returned to his work on mechanics, i.e., gravitation and its effect on the orbits of planets, with reference to Kepler's laws of planetary motion, and consulting with Hooke and Flamsteed on the subject. He published his results in De motu corporum in gyrum (1684). This contained the beginnings of the laws of motion that would inform the Principia.

The Philosophiae Naturalis Principia Mathematica (now known as the Principia) was published on 5 July 1687 with encouragement and financial help from Edmond Halley. In this work Newton stated the three universal laws of motion that were not to be improved upon for more than two hundred years. He used the Latin word gravitas (weight) for the effect that would become known as gravity, and defined the law of universal gravitation. In the same work he presented the first analytical determination, based on Boyle's law, of the speed of sound in air. Newton's postulate of an invisible force able to act over vast distances led to him being criticised for introducing "occult agencies" into science.^[24]

With the Principia, Newton became internationally recognised.^[25] He acquired a circle of admirers, including the Swiss-born mathematician Nicolas Fatio de Duillier, with whom he formed an intense relationship that lasted until 1693, when it abruptly ended, at the same time that Newton suffered a nervous breakdown.^[26]

Later life

In the 1690s, Newton wrote a number of religious tracts dealing with the literal interpretation of the Bible. Henry More's belief in the Universe and rejection of Cartesian dualism may have influenced Newton's religious ideas. A manuscript he sent to John Locke in which he disputed the existence of the Trinity was never published. Later works – The Chronology of Ancient Kingdoms Amended (1728) and Observations Upon the Prophecies of Daniel and the Apocalypse of St. John (1733) – were published after his death. He also devoted a great deal of time to alchemy (see above).

Newton was also a member of the Parliament of England from 1689 to 1690 and in 1701, but according to some accounts his only comments were to complain about a cold draught in the chamber and request that the window be closed.^[27]

Newton moved to London to take up the post of warden of the Royal Mint in 1696, a position that he had obtained through the patronage of Charles Montagu, 1st Earl of Halifax, then Chancellor of the Exchequer. He took charge of England's great recoining, somewhat treading on the toes of Master Lucas (and securing the job of deputy comptroller of the temporary Chester branch for Edmond Halley). Newton became perhaps the best-known Master of the Mint upon Lucas' death in 1699, a position Newton held until his death. These appointments were intended as sinecures, but Newton took them seriously, retiring from his Cambridge duties in 1701, and exercising his power to reform the currency and punish clippers and counterfeiters. As Master of the Mint in 1717 in the "Law of Queen Anne" Newton unintentionally moved the Pound Sterling from the silver standard to the gold standard by setting the bimetallic relationship between gold coins and the silver penny in favour of gold. This caused silver sterling coin to be melted and shipped out of Britain. Newton was made President of the Royal Society in 1703 and an associate of the French Académie des Sciences. In his position at the Royal Society, Newton made an enemy of John Flamsteed, the Astronomer Royal, by prematurely publishing Flamsteed's Historia Coelestis Britannica, which Newton had used in his studies.^[28]

In April 1705 Queen Anne knighted Newton during a royal visit to Trinity College, Cambridge. The knighthood is likely to have been motivated by political considerations connected with the Parliamentary election in May 1705, rather than any recognition of Newton's scientific work or services as Master of the Mint.^[29]

Newton died in London on 31 March 1727 [OS: 20 March 1726]^[1], and was buried in Westminster Abbey. His half-niece, Catherine Barton Conduitt,^[30] served as his hostess in social affairs at his house on Jermyn Street in London; he was her "very loving Uncle,"^[31] according to his letter to her when she was recovering from smallpox. Newton, who had no children, had divested much of his estate onto relatives in his last years, and died intestate.

After his death, Newton's body was discovered to have had massive amounts of mercury in it, probably resulting from his alchemical pursuits. Mercury poisoning could explain Newton's eccentricity in late life.^[32]

After death

Fame

French mathematician Joseph-Louis Lagrange often said that Newton was the greatest genius who ever lived, and once added that he was also "the most fortunate, for we cannot find more than once a system of the world to establish."^[33] English poet Alexander Pope was moved by Newton's accomplishments to write the famous epitaph:

Nature and nature's laws lay hid in night;
God said "Let Newton be" and all was light.

Newton himself was rather more modest of his own achievements, famously writing in a letter to Robert Hooke in February 1676:

If I have seen further it is by standing on ye shoulders of Giants^[34]

though historians generally think the above quote was an attack on Hooke (who was short and hunchbacked), rather than – or in addition to – a statement of modesty.^[35][36] The two were in a dispute over optical discoveries at the time. The latter interpretation also fits with many of his other disputes over his discoveries, such as the question of who discovered calculus as discussed above.

In a later memoir, Newton wrote:

I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.^[37]

Commemorations

Newton's monument (1731) can be seen in Westminster Abbey, at the north of the entrance to the choir against the choir screen. It was executed by the sculptor Michael Rysbrack (1694–1770) in white and grey marble with design by the architect William Kent (1685–1748). The monument features a figure of Newton reclining on top of a sarcophagus, his right elbow resting on several of his great books and his left hand pointing to a scroll with a mathematical design. Above him is a pyramid and a celestial globe showing the signs of the Zodiac and the path of the comet of 1680. A relief panel depicts putti using instruments such as a telescope and prism.^[38] The Latin inscription on the base translates as:

Here is buried Isaac Newton, Knight, who by a strength of mind almost divine, and mathematical principles peculiarly his own, explored the course and figures of the planets, the paths of comets, the tides of the sea, the dissimilarities in rays of light, and, what no other scholar has previously imagined, the properties of the colours thus produced. Diligent, sagacious and faithful, in his expositions of nature, antiquity and the holy Scriptures, he vindicated by his philosophy the majesty of God mighty and good, and expressed the simplicity of the Gospel in his manners. Mortals rejoice that there has existed such and so great an ornament of the human race! He was born on 25 December 1642, and died on 20 March 1726/7. — Translation from G.L. Smyth, The Monuments and Genii of St. Paul's Cathedral, and of Westminster Abbey (1826), ii, 703–4.^[38]

From 1978 until 1988, an image of Newton designed by Harry Ecclestone appeared on Series D £1 banknotes issued by the Bank of England (the last £1 notes to be issued by the Bank of England). Newton was shown on the reverse of the notes holding a book and accompanied by a telescope, a prism and a map of the Solar System.^[39]

A statue of Isaac Newton, standing over an apple, can be seen at the Oxford University Museum of Natural History.

Newton in popular culture

Religious views

Historian Stephen D. Snobelen says of Newton, "Isaac Newton was a heretic. But like Nicodemus, the secret disciple of Jesus, he never made a public declaration of his private faith – which the orthodox would have deemed extremely radical. He hid his faith so well that scholars are still unravelling his personal beliefs."^[40] Snobelen concludes that Newton was at least a Socinian sympathiser (he owned and had thoroughly read at least eight Socinian books), possibly an Arian and almost certainly an antitrinitarian.^[40] In an age notable for its religious intolerance there are few public expressions of Newton's radical views, most notably his refusal to take holy orders and his refusal, on his death bed, to take the sacrament when it was offered to him.^[40]

In a view disputed by Snobelen,^[40] T.C. Pfizenmaier argues that Newton held the Eastern Orthodox view of the Trinity rather than the Western one held by Roman Catholics, Anglicans, and most Protestants.^[41] In his own day, he was also accused of being a Rosicrucian (as were many in the Royal Society and in the court of Charles II).^[42]

Although the laws of motion and universal gravitation became Newton's best-known discoveries, he warned against using them to view the Universe as a mere machine, as if akin to a great clock. He said, "Gravity explains the motions of the planets, but it cannot explain who set the planets in motion. God governs all things and knows all that is or can be done."^[43]

His scientific fame notwithstanding, Newton's studies of the Bible and of the early Church Fathers were also noteworthy. Newton wrote works on textual criticism, most notably An Historical Account of Two Notable Corruptions of Scripture. He also placed the crucifixion of Jesus Christ at 3 April, AD 33, which agrees with one traditionally accepted date.^[44] He also attempted, unsuccessfully, to find hidden messages within the Bible.

In his own lifetime, Newton wrote more on religion than he did on natural science. He believed in a rationally immanent world, but he rejected the hylozoism implicit in Leibniz and Baruch Spinoza. Thus, the ordered and dynamically informed Universe could be understood, and must be understood, by an active reason. In his correspondence, Newton claimed that in writing the Principia "I had an eye upon such Principles as might work with considering men for the belief of a Deity".^[45] He saw evidence of design in the system of the world: "Such a wonderful uniformity in the planetary system must be allowed the effect of choice". But Newton insisted that divine intervention would eventually be required to reform the system, due to the slow growth of instabilities.^[46] For this Leibniz lampooned him: "God Almighty wants to wind up his watch from time to time: otherwise it would cease to move. He had not, it seems, sufficient foresight to make it a perpetual motion." ^[47] Newton's position was vigorously defended by his follower Samuel Clarke in a famous correspondence.

Effect on religious thought

Newton and Robert Boyle’s mechanical philosophy was promoted by rationalist pamphleteers as a viable alternative to the pantheists and enthusiasts, and was accepted hesitantly by orthodox preachers as well as dissident preachers like the latitudinarians.^[48] Thus, the clarity and simplicity of science was seen as a way to combat the emotional and metaphysical superlatives of both superstitious enthusiasm and the threat of atheism,^[49] and, at the same time, the second wave of English deists used Newton's discoveries to demonstrate the possibility of a "Natural Religion."

The attacks made against pre-Enlightenment "magical thinking," and the mystical elements of Christianity, were given their foundation with Boyle’s mechanical conception of the Universe. Newton gave Boyle’s ideas their completion through mathematical proofs and, perhaps more importantly, was very successful in popularising them.^[50] Newton refashioned the world governed by an interventionist God into a world crafted by a God that designs along rational and universal principles.^[51] These principles were available for all people to discover, allowed people to pursue their own aims fruitfully in this life, not the next, and to perfect themselves with their own rational powers.^[52]

Newton saw God as the master creator whose existence could not be denied in the face of the grandeur of all creation.^[53][54][55] His spokesman, Clarke, rejected Leibniz' theodicy which cleared God from the responsibility for "l'origine du mal" by making God removed from participation in his creation, since as Clarke pointed out, such a deity would be a king in name only, and but one step away from atheism.^[56] But the unforeseen theological consequence of the success of Newton's system over the next century was to reinforce the deist position advocated by Leibniz.^[57] The understanding of the world was now brought down to the level of simple human reason, and humans, as Odo Marquard argued, became responsible for the correction and elimination of evil.^[58]

On the other hand, latitudinarian and Newtonian ideas taken too far resulted in the millenarians, a religious faction dedicated to the concept of a mechanical Universe, but finding in it the same enthusiasm and mysticism that the Enlightenment had fought so hard to extinguish.^[59]

Views of the end of the world

In a manuscript he wrote in 1704 in which he describes his attempts to extract scientific information from the Bible, he estimated that the world would end no earlier than 2060. In predicting this he said, "This I mention not to assert when the time of the end shall be, but to put a stop to the rash conjectures of fanciful men who are frequently predicting the time of the end, and by doing so bring the sacred prophesies into discredit as often as their predictions fail."^[60]

Enlightenment philosophers

Enlightenment philosophers chose a short history of scientific predecessors — Galileo, Boyle, and Newton principally — as the guides and guarantors of their applications of the singular concept of Nature and Natural Law to every physical and social field of the day. In this respect, the lessons of history and the social structures built upon it could be discarded.^[61]

It was Newton’s conception of the Universe based upon Natural and rationally understandable laws that became one of the seeds for Enlightenment ideology.^[62] Locke and Voltaire applied concepts of Natural Law to political systems advocating intrinsic rights; the physiocrats and Adam Smith applied Natural conceptions of psychology and self-interest to economic systems and the sociologists criticised the current social order for trying to fit history into Natural models of progress. Monboddo and Samuel Clarke resisted elements of Newton's work, but eventually rationalised it to conform with their strong religious views of nature.

Newton and the counterfeiters

As warden of the Royal Mint, Newton estimated that 20% of the coins taken in during The Great Recoinage were counterfeit. Counterfeiting was high treason, punishable by being hanged, drawn and quartered. Despite this, convictions of the most flagrant criminals could be extremely difficult to achieve; however, Newton proved to be equal to the task.^[63] Disguised as an habitué of bars and taverns, he gathered much of that evidence himself.^[64] For all the barriers placed to prosecution, and separating the branches of government, English law still had ancient and formidable customs of authority. Newton was made a justice of the peace and between June 1698 and Christmas 1699 conducted some 200 cross-examinations of witnesses, informers and suspects. Newton won his convictions and in February 1699, he had ten prisoners waiting to be executed.^{[citation needed]}

One of Newton's cases as the King's attorney was against William Chaloner.^[65] Chaloner's schemes included setting up phony conspiracies of Catholics and then turn in the hapless conspirators whom he entrapped. Chaloner made himself rich enough to posture as a gentleman. Petitioning Parliament, Chaloner accused the Mint of providing tools to counterfeiters (a charge also made by others). He proposed that he be allowed to inspect the Mint's processes in order to improve them. He petitioned Parliament to adopt his plans for a coinage that could not be counterfeited, while at the same time striking false coins.^[66] Newton put Chaloner on trial for counterfeiting and had him sent to Newgate Prison in September 1697, but Chaloner had friends in high places who helped him to secure an acquittal and his release.^[67] Newton put him on trial a second time with conclusive evidence. Chaloner was convicted of high treason and hanged, drawn and quartered on 23 March 1699 at Tyburn gallows.^[68]

Newton's laws of motion

Classical mechanics

Newton's Second Law

History of ... Fundamental concepts Space · Time · Mass · Force Energy · Momentum Formulations Newtonian mechanics Lagrangian mechanics Hamiltonian mechanics Branches Statics Dynamics Kinematics Applied mechanics Celestial mechanics Continuum mechanics Statistical mechanics Scientists Newton · Euler · d'Alembert · Clairaut Lagrange · Laplace · Hamilton · Poisson

This box: view • talk • edit

The famous three laws of motion:

Newton's First Law (also known as the Law of Inertia) states that an object at rest tends to stay at rest and that an object in uniform motion tends to stay in uniform motion unless acted upon by a net external force.

Newton's Second Law states that an applied force, 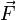, on an object equals the rate of change of its momentum, 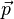, with time. Mathematically, this is expressed as

Since the second law applies to a system with constant mass (dm/dt = 0), the first term vanishes, and the equation can be written in the iconic form

The first and second laws represent a break with the physics of Aristotle, in which it was believed that a force was necessary in order to maintain motion. They state that a force is only needed in order to change an object's state of motion. The SI unit of force is the newton, named in Newton's honour.

Newton's Third Law states that for every action there is an equal and opposite reaction. This means that any force exerted onto an object has a counterpart force that is exerted in the opposite direction back onto the first object. A common example is of two ice skaters pushing against each other and sliding apart in opposite directions. Another example is the recoil of a firearm, in which the force propelling the bullet is exerted equally back onto the gun and is felt by the shooter. Since the objects in question do not necessarily have the same mass, the resulting acceleration of the two objects can be different (as in the case of firearm recoil).

Unlike Aristotle's, Newton's physics is meant to be universal. For example, the second law applies both to a planet and to a falling stone.

The vector nature of the second law addresses the geometrical relationship between the direction of the force and the manner in which the object's momentum changes. Before Newton, it had typically been assumed that a planet orbiting the sun would need a forward force to keep it moving. Newton showed instead that all that was needed was an inward attraction from the sun. Even many decades after the publication of the Principia, this counterintuitive idea was not universally accepted, and many scientists preferred Descartes' theory of vortices.^[69]

Newton's apple

Newton himself often told that story that he was inspired to formulate his theory of gravitation by watching the fall of an apple from a tree.^[70]

Cartoons have gone further to suggest the apple actually hit Newton's head, and that its impact somehow made him aware of the force of gravity. It is known from his notebooks that Newton was grappling in the late 1660s with the idea that terrestrial gravity extends, in an inverse-square proportion, to the Moon; however it took him two decades to develop the full-fledged theory.^[71] John Conduitt, Newton's assistant at the Royal Mint and husband of Newton's niece, described the event when he wrote about Newton's life:

In the year 1666 he retired again from Cambridge to his mother in Lincolnshire. Whilst he was pensively meandering in a garden it came into his thought that the power of gravity (which brought an apple from a tree to the ground) was not limited to a certain distance from earth, but that this power must extend much further than was usually thought. Why not as high as the Moon said he to himself & if so, that must influence her motion & perhaps retain her in her orbit, whereupon he fell a calculating what would be the effect of that supposition.^[72]

The question was not whether gravity existed, but whether it extended so far from Earth that it could also be the force holding the moon to its orbit. Newton showed that if the force decreased as the inverse square of the distance, one could indeed calculate the Moon's orbital period, and get good agreement. He guessed the same force was responsible for other orbital motions, and hence named it "universal gravitation".

A contemporary writer, William Stukeley, recorded in his Memoirs of Sir Isaac Newton's Life a conversation with Newton in Kensington on 15 April 1726, in which Newton recalled "when formerly, the notion of gravitation came into his mind. It was occasioned by the fall of an apple, as he sat in contemplative mood. Why should that apple always descend perpendicularly to the ground, thought he to himself. Why should it not go sideways or upwards, but constantly to the Earth's centre." In similar terms, Voltaire wrote in his Essay on Epic Poetry (1727), "Sir Isaac Newton walking in his gardens, had the first thought of his system of gravitation, upon seeing an apple falling from a tree."

Various trees are claimed to be "the" apple tree which Newton describes. The King's School, Grantham, claims that the tree was purchased by the school, uprooted and transported to the headmaster's garden some years later, the staff of the [now] National Trust-owned Woolsthorpe Manor dispute this, and claim that a tree present in their gardens is the one described by Newton. A descendant of the original tree can be seen growing outside the main gate of Trinity College, Cambridge, below the room Newton lived in when he studied there. The National Fruit Collection at Brogdale^[73] can supply grafts from their tree, which appears identical to Flower of Kent, a coarse-fleshed cooking variety.^[74]

Writings by Newton

• Method of Fluxions (1671)
• Of Natures Obvious Laws & Processes in Vegetation (unpublished, c. 1671–75)^[75]
• De Motu Corporum in Gyrum (1684)
• Philosophiae Naturalis Principia Mathematica (1687)
• Opticks (1704)
• Reports as Master of the Mint (1701–25)
• Arithmetica Universalis (1707)
• The System of the World, Optical Lectures, The Chronology of Ancient Kingdoms, (Amended) and De mundi systemate (published posthumously in 1728)
• Observations on Daniel and The Apocalypse of St. John (1733)
• An Historical Account of Two Notable Corruptions of Scripture (1754)

See also

Footnotes and references

References

• Ball, W.W. Rouse (1908). A Short Account of the History of Mathematics. New York: Dover. 
• Christianson, Gale (1984). In the Presence of the Creator: Isaac Newton & His Times. New York: Free Press. ISBN 0-02-905190-8.  This well documented work provides, in particular, valuable information regarding Newton's knowledge of Patristics
• Craig, John (1958). "Isaac Newton – Crime Investigator". Nature 182: 149. doi:10.1038/182149a0. 
• Craig, John (1963). "Isaac Newton and the Counterfeiters". Notes and Records of the Royal Society of London 18: 136. doi:10.1098/rsnr.1963.0017. 
• Westfall, Richard S. (1980, 1998). Never at Rest. Cambridge University Press. ISBN 0-521-27435-4. 
• Westfall, Richard S. (1994). The Life of Isaac Newton. Cambridge University Press. ISBN 0-521-47737-9. 
• White, Michael (1997). Isaac Newton: The Last Sorcerer. Fourth Estate Limited. ISBN 1-85702-416-8. 
• "Sir Isaac Newton". School of Mathematics and Statistics, University of St. Andrews, Scotland. http://www-history.mcs.st-andrews.ac.uk/Mathematicians/Newton.html. Retrieved on 2005-03-08. 
• "The Newton Project". Imperial College London. http://www.newtonproject.sussex.ac.uk/prism.php?id=1. Retrieved on 2005-03-08. 

Further reading

This article may be too long to comfortably read and navigate. Please consider splitting content into sub-articles and using this article for a summary of the key points of the subject. (March 2009)

• Andrade, E. N. De C. (1950). Isaac Newton. New York: Chanticleer Press. 
• Bardi, Jason Socrates. The Calculus Wars: Newton, Leibniz, and the Greatest Mathematical Clash of All Time. (2006). 277 pp. excerpt and text search
• Bechler, Zev (1991). Newton's Physics and the Conceptual Structure of the Scientific Revolution. Springer. ISBN 0792310543. .
• Berlinski, David. Newton's Gift: How Sir Isaac Newton Unlocked the System of the World. (2000). 256 pp. excerpt and text search ISBN 0-684-84392-7
• Buchwald, Jed Z. and Cohen, I. Bernard, eds. Isaac Newton's Natural Philosophy. MIT Press, 2001. 354 pp. excerpt and text search
• Casini, P. (1988). "Newton's Principia and the Philosophers of the Enlightenment". Notes and Records of the Royal Society of London 42 (1): 35–52. doi:10.1098/rsnr.1988.0006. ISSN 0035–9149. http://links.jstor.org/sici?sici=0035-9149%28198801%2942%3A1%3C35%3AN%27ATPO%3E2.0.CO%3B2-H. 
• Christianson, Gale E. (1996). Isaac Newton and the Scientific Revolution. Oxford U. Press. ISBN 019530070X.  See this site for excerpt and text search.
• Christianson, Gale (1984). In the Presence of the Creator: Isaac Newton & His Times. New York: Free Press. ISBN 0-02-905190-8. 
• Cohen, I. Bernard and Smith, George E., ed. The Cambridge Companion to Newton. (2002). 500 pp. focuses on philosophical issues only; excerpt and text search; complete edition online
• Cohen, I. B. (1980). The Newtonian Revolution. Cambridge: Cambridge University Press. 
• Craig, John (1946). Newton at the Mint. Cambridge, England: Cambridge University Press. 
• Dampier, William C.; Dampier, M. (1959). Readings in the Literature of Science. New York: Harper & Row. 
• de Villamil, Richard (1931). Newton, the Man. London: G.D. Knox.  – Preface by Albert Einstein. Reprinted by Johnson Reprint Corporation, New York (1972).
• Dobbs, B. J. T. (1975). The Foundations of Newton's Alchemy or "The Hunting of the Greene Lyon". Cambridge: Cambridge University Press. 
• Gjertsen, Derek (1986). The Newton Handbook. London: Routledge & Kegan Paul. ISBN 0-7102-0279-2. 
• Gleick, James (2003). Isaac Newton. Alfred A. Knopf. ISBN 0375422331. 
• Halley, E. (1687). "Review of Newton's Principia". Philosophical Transactions 186: 291 – 297. 
• Hart, Michael H. (1992). The 100''. Carol Publishing Group. ISBN 0-8065-1350-0.  – paperback
• Hawking, Stephen, ed. On the Shoulders of Giants. ISBN 0-7624-1348-4 Places selections from Newton's Principia in the context of selected writings by Copernicus, Kepler, Galileo and Einstein
• Herivel, J. W. (1965). The Background to Newton's Principia. A Study of Newton's Dynamical Researches in the Years 1664–84. Oxford: Clarendon Press. 
• Keynes, John Maynard (1963). Essays in Biography. W. W. Norton & Co. ISBN 0-393-00189-X.  Keynes took a close interest in Newton and owned many of Newton's private papers.
• Koyré, A. (1965). Newtonian Studies. Chicago: University of Chicago Press. 
• Newton, Isaac. Papers and Letters in Natural Philosophy, edited by I. Bernard Cohen. Harvard University Press, 1958,1978. ISBN 0-674-46853-8.
• Newton, Isaac (1642–1727). The Principia: a new Translation, Guide by I. Bernard Cohen ISBN 0-520-08817-4 University of California (1999)
• Pemberton, H. (1728). A View of Sir Isaac Newton's Philosophy. London: S. Palmer. 
• Shamos, Morris H. (1959). Great Experiments in Physics. New York: Henry Holt and Company, Inc.. 
• Shapley, Harlow, S. Rapport, and H. Wright. A Treasury of Science; "Newtonia" pp. 147–9; "Discoveries" pp. 150–4. Harper & Bros., New York, (1946).
• Simmons, J. (1996). The Giant Book of Scientists  – The 100 Greatest Minds of all Time. Sydney: The Book Company. 
• Stukeley, W. (1936), Memoirs of Sir Isaac Newton's Life, London: Taylor and Francis  (edited by A. H. White; originally published in 1752)
• Westfall, R. S. (1971). Force in Newton's Physics: The Science of Dynamics in the Seventeenth Century. London: Macdonald. 

Newton and religion

• Dobbs, Betty Jo Tetter. The Janus Faces of Genius: The Role of Alchemy in Newton's Thought. (1991), links the alchemy to Arianism
• Force, James E., and Richard H. Popkin, eds. Newton and Religion: Context, Nature, and Influence. (1999), 342pp . Pp. xvii + 325. 13 papers by scholars using newly opened manuscripts
• Ramati, Ayval. "The Hidden Truth of Creation: Newton's Method of Fluxions" British Journal for the History of Science 34: 417–438. in JSTOR, argues that his calculus had a theological basis
• Snobelen, Stephen D. "'God of Gods, and Lord of Lords': The Theology of Isaac Newton's General Scholium to the Principia," Osiris, 2nd Series, Vol. 16, (2001), pp. 169–208 in JSTOR
• Snobelen, Stephen D. "Isaac Newton, Heretic: The Strategies of a Nicodemite," British Journal for the History of Science 32: 381–419. in JSTOR
• Pfizenmaier, Thomas C. "Was Isaac Newton an Arian?," Journal of the History of Ideas, Vol. 58, No. 1 (Jan., 1997), pp. 57–80 in JSTOR
• Westfall, Richard S. Never at Rest: A Biography of Isaac Newton. 2 vol. Cambridge U. Press, 1981. 895 pp. the major scholarly biography excerpt and text search
• Wiles, Maurice. Archetypal Heresy. Arianism through the Centuries. (1996) 214pp, with chapter 4 on 18th century England; pp 77–93 on Newtorn excerpt and text search,

Primary sources

• Newton, Isaac. The Principia: Mathematical Principles of Natural Philosophy. U. of California Press, (1999). 974 pp.
  • Brackenridge, J. Bruce. The Key to Newton's Dynamics: The Kepler Problem and the Principia: Containing an English Translation of Sections 1, 2, and 3 of Book One from the First (1687) Edition of Newton's Mathematical Principles of Natural Philosophy. U. of California Press, 1996. 299 pp.
• Newton, Isaac. The Optical Papers of Isaac Newton. Vol. 1: The Optical Lectures, 1670–1672. Cambridge U. Press, 1984. 627 pp.
  • Newton, Isaac. Opticks (4th ed. 1730) online edition
  • Newton, I. (1952). Opticks, or A Treatise of the Reflections, Refractions, Inflections & Colours of Light. New York: Dover Publications.
• Newton, I. Sir Isaac Newton's Mathematical Principles of Natural Philosophy and His System of the World, tr. A. Motte, rev. Florian Cajori. Berkeley: University of California Press. (1934).
• Whiteside, D. T. (1967–82). The Mathematical Papers of Isaac Newton. Cambridge: Cambridge University Press.  – 8 volumes
• Newton, Isaac. The correspondence of Isaac Newton, ed. H. W. Turnbull and others, 7 vols. (1959–77).
• Newton's Philosophy of Nature: Selections from His Writings edited by H. S. Thayer, (1953), online edition
• Isaac Newton, Sir; J Edleston; Roger Cotes, Correspondence of Sir Isaac Newton and Professor Cotes, including letters of other eminent men, London, John W. Parker, West Strand; Cambridge, John Deighton, 1850. – Google Books
• Maclaurin, C. (1748). An Account of Sir Isaac Newton's Philosophical Discoveries, in Four Books. London: A. Millar and J. Nourse.
• Newton, I. (1958). Isaac Newton's Papers and Letters on Natural Philosophy and Related Documents, eds. I. B. Cohen and R. E. Schofield. Cambridge: Harvard University Press.
• Newton, I. (1962). The Unpublished Scientific Papers of Isaac Newton: A Selection from the Portsmouth Collection in the University Library, Cambridge, ed. A. R. Hall and M. B. Hall. Cambridge: Cambridge University Press.
• Newton, I. (1975). Isaac Newton's 'Theory of the Moon's Motion' (1702). London: Dawson.

External links

This article's external links may not follow Wikipedia's content policies or guidelines. Please improve this article by removing excessive or inappropriate external links.

• ScienceWorld biography
• Dictionary of Scientific Biography
• The Newton Project
• Newton's Principia – read and search
• Rebuttal of Newton's astrology
• Newton's Religious Views Reconsidered
• Descartes, Space, and Body, an excerpt from De Gravitatione et Aequipondio Fluidorum, with annotations by Jonathan Bennett
• 5 March–12 June 2005 Isaac Newton's personal copy of Principia at Huntington Library
• Newton's Royal Mint Reports
• Newton's Dark Secrets NOVA TV programme.
• O'Connor, John J.; Robertson, Edmund F., "Isaac Newton", MacTutor History of Mathematics archive 
• from The Stanford Encyclopedia of Philosophy:
  • Issac Newton, by George Smith
  • Newton's Philosophiae Naturalis Principia Mathematica, by George Smith
  • Newton's Philosophy, by Andrew Janiak
  • Newton's views on space, time, and motion, by Robert Rynasiewicz
• Newton's Castle Educational material
• The Chymistry of Isaac Newton Research on his Alchemical writings
• FMA Live! Cool program for teaching Newton's laws to kids
• Newton's religious position
• The "General Scholium" to Newton's Principia
• Kandaswamy, Anand M. The Newton/Leibniz Conflict in Context
• The Mind of Isaac Newton By combining images, audio, animations and interactive segments, the application gives students a sense of Newton's multifaceted mind.
• Works by Isaac Newton at Project Gutenberg
• Newton's First ODE – A study by Phaser Scientific Software on how Newton approximated the solutions of a first-order ODE using infinite series
•  "Newton, Sir Isaac". Encyclopædia Britannica (11th ed.). 1911. 

Parliament of England
Preceded by Robert Brady	Member of Parliament for Cambridge University with Robert Sawyer 1689–1690	Succeeded by Edward Finch
Preceded by Anthony Hammond	Member of Parliament for Cambridge University with Henry Boyle 1701–1702	Succeeded by Arthur Annesley
Government offices
Preceded by Thomas Neale	Master of the Mint 1700 – 1727	Succeeded by John Conduitt

v • d • e Lucasian Professors of Mathematics Isaac Barrow (1664) · Isaac Newton (1669) · William Whiston (1702) · Nicholas Saunderson (1711) · John Colson (1739) · Edward Waring (1760) · Isaac Milner (1798) · Robert Woodhouse (1820) · Thomas Turton (1822) · George Biddell Airy (1826) · Charles Babbage (1828) · Joshua King (1839) · George Stokes (1849) · Joseph Larmor (1903) · Paul Dirac (1932) · James Lighthill (1969) · Stephen Hawking (1979)

v • d • e Presidents of the Royal Society Isaac Newton (1703) · Hans Sloane (1727) · Martin Folkes (1741) · George Parker (1752) · James Douglas (1764) · James Burrow (1768) · James West (1768) · James Burrow (1772) · John Pringle (1772) · Joseph Banks (1778) Complete roster: 1600s · 1700s · 1800s · 1900s · 2000s

v • d • e Figures in the Age of Enlightenment by country   Notable Figures British Colonies Benjamin Franklin · Thomas Jefferson · James Madison · Thomas Paine Prussia and Saxe-Weimar Immanuel Kant · Gotthold Ephraim Lessing · Johann Gottfried von Herder · Johann Wolfgang von Goethe · J.C.F. von Schiller · Moses Mendelssohn England Edward Gibbon · Samuel Johnson · Mary Wollstonecraft · John Locke  · Isaac Newton · Thomas Hobbes Scotland Joseph Black · James Boswell · Adam Ferguson · David Hume · Thomas Reid · Adam Smith France Montesquieu · François Quesnay · Voltaire · Buffon · Jean-Jacques Rousseau · Denis Diderot · Helvétius · Jean le Rond d'Alembert · Baron d'Holbach · Marquis de Sade · Condorcet · Étienne Bonnot de Condillac Italy Cesare Beccaria Greek Enlightenment Adamantios Korais · Rigas Feraios   Related topics Atheism · Capitalism · Civil liberties · Critical thinking · Deism · Democracy · Empiricism · Enlightened absolutism · Free markets · Haskalah · Humanism · Liberalism · Natural philosophy · Rationality · Reason · Sapere aude · Science · Socialism · Secularism · French Encyclopédistes · German Classicism

v • d • e Metaphysics Topics Time  · Experience  · Causality  · Principle  · Will  · Quality  · Value  · Self  · Action  · Intention  · Matter  · Meaning  · Essence  · Subject  · Object  · Unity  · Truth  · Mind  · Necessity  · Pattern  · Type  · Motion  · Freedom  · Form  · Idea  · Modality  · Substance  · Properties  · more...  · Ontology Being  · Category of being  · Change  · Cogito ergo sum  · Dualism  · Embodied philosophy  · Entity  · Existence  · Existentialism  · Identity  · Physical object  · Properties  · Reality  · Relativism  · Scientific realism  · Subjectivism  · Substance theory  · Universal  · Unobservables  · Teleology Big Questions What is the nature of the universe?  · What is the meaning of life?  · What is being?  · What is time?  · What is experience?  · What is causality?  · What are principles?  · What is value?  · What is the self?  · What is action?  · What is will?  · Whats is matter?  · What is meaning?  · What are types?  · Metaphysical theories Platonic idealism  · Hindu idealism  · Scientific materialism  · Cartesian dualism  · Phenomenalism  · Existentialism  · Nihilism  · Realism  · Anti-realism  · Determinism  · Solipsism  · Physicalism  · MOQ Metaphysicians Aristotle · Thomas Aquinas · George Berkeley · Donald Davidson · René Descartes · Georg W. F. Hegel · Martin Heidegger · Immanuel Kant · Saul Kripke · Gottfried Leibniz · John Locke · George Edward Moore · Isaac Newton · Plato · Plotinus · Hilary Putnam · Willard V. O. Quine · Bertrand Russell · Parmenides · Jean-Paul Sartre · Arthur Schopenhauer · John Duns Scotus · Baruch Spinoza · Alfred N. Whitehead · Ludwig Wittgenstein · Portal · Category · Task Force · Stubs · Discussion

Persondata
NAME	Newton, Isaac
ALTERNATIVE NAMES	Newton, Sir Isaac
SHORT DESCRIPTION	English mathematician, physicist, and astronomer
DATE OF BIRTH	4 January 1643(1643-01-04)
PLACE OF BIRTH	Woolsthorpe-by-Colsterworth, Lincolnshire, England
DATE OF DEATH	31 March 1727
PLACE OF DEATH	Kensington, London, England