Harmonic

From Wikipedia, the free encyclopedia

In acoustics and telecommunication, a harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency. For example, if the fundamental frequency is f, the harmonics have frequencies f, 2f, 3f, 4f, etc. The harmonics have the property that they are all periodic at the fundamental frequency, therefore the sum of harmonics is also periodic at that frequency. Harmonic frequencies are equally spaced by the width of the fundamental frequency and can be found by repeatedly adding that frequency. For example, if the fundamental frequency is 25 Hz, the frequencies of the harmonics are: 25 Hz, 50 Hz, 75 Hz, 100 Hz, etc.

[edit] Characteristics

Many oscillators, including the human voice, a bowed violin string, or a Cepheid variable star, are more-or-less periodic, and thus can be decomposed into harmonics.

Most passive oscillators, such as a plucked guitar string or a struck drum head or struck bell, naturally oscillate at several frequencies known as partials. When the oscillator is long and thin, such as a guitar string, a trumpet, or a chime, the partials are practically integer multiples of the fundamental frequency. Hence, these devices can mimic the sound of singing and are often incorporated into music. Partials whose frequencies are not integer multiples of the fundamental are called inharmonic and are sometimes perceived as unpleasant.

The untrained human ear typically does not perceive harmonics as separate notes. Instead, they are perceived as the timbre of the tone. Bells have more clearly perceptible partials than most instruments. Antique singing bowls are well known for their unique quality of producing multiple harmonic partials or multiphonics.

[edit] Harmonics and overtones

The tight relation between overtones and harmonics in music often leads to their being used synonymously in a strictly musical context, but they are counted differently leading to some possible confusion. This chart demonstrates how they are counted:

In many musical instruments, it is possible to play the upper harmonics without the fundamental note being present. In a simple case (e.g. recorder) this has the effect of making the note go up in pitch by an octave; but in more complex cases many other pitch variations are obtained. In some cases it also changes the timbre of the note. This is part of the normal method of obtaining higher notes in wind instruments, where it is called overblowing. The extended technique of playing multiphonics also produces harmonics. On string instruments it is possible to produce very pure sounding notes, called harmonics or flageolets by string players, which have an eerie quality, as well as being high in pitch. Harmonics may be used to check at a unison the tuning of strings that are not tuned to the unison. For example, lightly fingering the node found half way down the highest string of a cello produces the same pitch as lightly fingering the node 1/3 of the way down the second highest string. For the human voice see Overtone singing, which uses harmonics.

Harmonics may be either used or considered as the basis of just intonation systems. Composer Arnold Dreyblatt is able to bring out different harmonics on the single string of his modified double bass by slightly altering his unique bowing technique halfway between hitting and bowing the strings. Composer Lawrence Ball uses harmonics to generate music electronically.

The fundamental frequency is the reciprocal of the period of the periodic phenomenon.

This article contains material from the Federal Standard 1037C, which, as a work of the United States Government, is in the public domain.

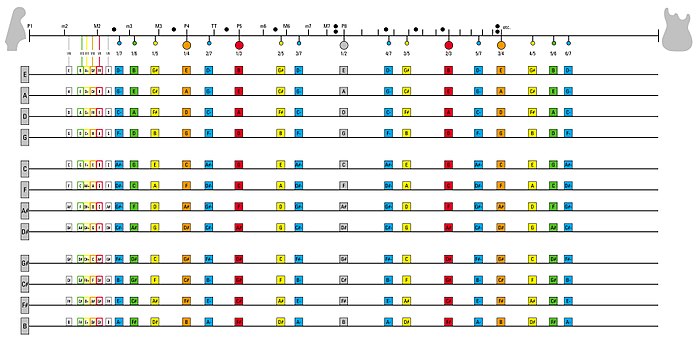
[edit] Harmonics on stringed instruments

playing a harmonic on a string (click to enlarge)

The following table displays the stop points on a stringed instrument, such as the guitar, at which gentle touching of a string will force it into a harmonic mode when vibrated.

[edit] Table of harmonics

Table of harmonics of a stringed instrument with colored dots indicating which positions can be lightly fingered to generate just intervals up to the 7th harmonic

[edit] Audio Samples

	Violin harmonics Violin natural harmonic stop points on the A string Harmonics 110x16 Demonstration of harmonics using electronic sine tones - fundamental and 15 harmonics of 110 Hz, 0.5s each. Note that each harmonic is presented at the same signal level as the fundamental; the sample tones sound louder as they increase in frequency
Problems listening to these files? See media help.

[edit] See also