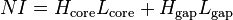Electromagnet

From Wikipedia, the free encyclopedia

An electromagnet is a type of magnet in which the magnetic field is produced by the flow of electric current. The magnetic field disappears when the current ceases.

Electromagnet attracts paper clips when current is applied creating a magnetic field, loses them when current and magnetic field are removed

[edit] Introduction

A wire with an electric current passing through it, generates a magnetic field around it, this is a simple electromagnet. The strength of magnetic field generated is proportional to the amount of current.

Current (I) through a wire produces a magnetic field (B). The field is oriented according to the right-hand rule.

In order to concentrate the magnetic field generated by a wire, it is commonly wound into a coil, where many turns of wire sit side by side. The magnetic field of all the turns of wire passes through the center of the coil. A coil forming the shape of a straight tube, a helix (similar to a corkscrew) is called a solenoid; a solenoid that is bent into a donut shape so that the ends meet is a toroid. Much stronger magnetic fields can be produced if a "core" of ferromagnetic material, such as soft iron, is placed inside the coil. The core magnifies the magnetic field to thousands of times the strength of the field of the coil alone. This is called a ferromagnetic-core or iron-core electromagnet.

The direction of the magnetic field through a coil of wire can be found from a form of the right-hand rule.^[1]^[2]^[3]^[4]^[5]^[6] If the fingers of the right hand are curled around the coil in the direction of current flow (conventional current, flow of positive charge) through the windings, the thumb points in the direction of the field inside the coil. The side of the magnet that the field lines emerge from is defined to be the north pole.

The main advantage of an electromagnet over a permanent magnet is that the magnetic field can be rapidly manipulated over a wide range by controlling the amount of electric current. However, a continuous supply of electrical energy is required to maintain the field.

Magnetic field produced by a solenoid. The crosses are wires in which current is moving into the page; the dots are wires in which current is moving up out of the page.

[edit] How electromagnets work

Iron is composed of small regions called magnetic domains that act like tiny magnets. Before the current in the electromagnet is turned on, the domains in the iron core point in random directions, so their tiny magnetic fields cancel each other out, and the iron has no large scale magnetic field. When a current is passed through the wire wrapped around the iron, its magnetic field penetrates the iron, and causes the domains to turn, aligning parallel to the magnetic field, so their tiny magnetic fields add to the wire's field, creating a large magnetic field that extends into the space around the magnet. The larger the current passed through the wire coil, the more the domains align, and the stronger the magnetic field is. Finally all the domains are aligned and further increases in current only cause slight increases in the magnetic field. This is called saturation.

When the current in the coil is turned off, most of the domains lose alignment and return to a random state and the field disappears. However in some materials some of the alignment persists, because the domains have difficulty turning their direction of magnetization, leaving the core a weak permanent magnet. This phenomenon is called hysteresis and the remaining magnetic field is called remanent magnetism.

[edit] History

Sturgeon's electromagnet, 1823

Danish scientist Hans Christian Ørsted discovered in 1820 that electric currents create magnetic fields. British scientist William Sturgeon invented the electromagnet in 1823.^[7]^[8] His first electromagnet was a horseshoe-shaped piece of iron that was wrapped with about 18 turns of bare copper wire (insulated wire didn't exist yet). The iron was varnished to insulate it from the windings. When a current was passed through the coil, the iron became magnetized and when the current was stopped, it was de-magnetized. Sturgeon displayed its power by showing that although it only weighed seven ounces, it could lift nine pounds when the current of a single-cell battery was applied. However, Sturgeon's magnets were weak because the uninsulated wire he used could only be wrapped in a single spaced out layer around the core, limiting the number of turns. Beginning in 1827, US scientist Joseph Henry systematically improved and popularized the electromagnet.^[9] By using wire insulated by silk thread he was able to wind multiple layers of wire on cores, creating powerful magnets with thousands of turns of wire, including one that could support 2063 pounds. The first major use for electromagnets was in telegraph sounders.

[edit] Analysis of ferromagnetic electromagnets

For definitions of the variables below, see box at end of article.

Industrial electromagnet lifting scrap iron, 1914

The magnetic field of electromagnets in the general case is given by Ampere's Law:

$\int \mathbf{J}\cdot d\mathbf{A} = \oint \mathbf{H}\cdot d\mathbf{l}$

which says that the integral of the magnetizing field H around any closed loop of the field is equal to the sum of the current flowing through the loop. Another equation used, that gives the magnetic field due to each small segment of current, is the Biot-Savart law. Computing the magnetic field and force exerted by ferromagnetic materials is difficult for two reasons. First, because the geometry of the field is complicated, particularly outside the core and in air gaps, where fringing fields and leakage flux must be considered. Second, because the magnetic field B and force are nonlinear functions of the current, depending on the nonlinear relation between B and H for the particular core material used. For precise calculations the finite element method is used.

[edit] Magnetic circuit - the constant B field approximation

However, in analyzing a typical DC electromagnet in which the magnetic field path is confined to a single loop or circuit most of which is in core material, the equations can be simplified. A common simplifying assumption, which will be used in this section, is that the magnetic field strength B is constant around the magnetic circuit. Most of the magnetic field will be concentrated in the core material. Within the core the magnetic field will be approximately uniform across any cross section, so if in addition the core has roughly constant area throughout its length, the field in the core will be constant. This just leaves the air gaps, if any, between core sections. In the gaps the magnetic field lines are no longer confined by the core, so they 'bulge' out beyond the outlines of the core before curving back to enter the next piece of core material, reducing the field strength in the gap. The bulges are called fringing fields. However, as long as the length of the gap is smaller than the cross section dimensions of the core, the field in the gap will be approximately the same as in the core. In addition, if parts of the core are too near other parts, some of the magnetic field lines will take 'short cuts' and not pass through the entire core circuit. This also occurs in the field near the windings, if the windings are not wrapped tightly around the core. This is called leakage flux. It also results in a lower magnetic field in the core. Therefore the equations in this section are valid for electromagnets for which:

the magnetic circuit is a single loop.
the core has roughly the same cross sectional area throughout its length.
the air gaps between sections of core material are not large compared with the cross sectional dimensions of the core.
there is negligible leakage flux

The main nonlinear feature of ferromagnetic materials is that the B field saturates at a certain value, which is around 1.6 teslas (T) for most high permeability core steels. The B field increases quickly with increasing current up to that value, but above that value the field levels off and increases at the much smaller paramagnetic value, regardless of how much current is sent through the windings. So the strength of the magnetic field possible from an iron core electromagnet is limited to 1.6-2 T.

[edit] Magnetic field created by a current

The magnetic field created by an electromagnet is proportional to both the number of turns in the winding, N, and the current in the wire, I, hence this product, NI, in ampere-turns, is given the name magnetomotive force. At first glance, therefore, it might appear that one could double the strength of an electromagnet either by doubling the number of turns, or doubling the current flowing; however, the problem is actually much more complex. To begin with, more turns require more lengths of wire, adding proportionately more resistance, which reduces the current; while raising the current raises heat and requires thicker wire, thus reducing the number of turns that fit into a given space; and raising voltage to raise current eventually requires thicker insulation, again reducing turns.

For an electromagnet with a single magnetic circuit, of which length L_core is in the core material and length L_gap is in air gaps, Ampere's Law reduces to:^[10]^[11]

$NI = H_{\mathrm{core}} L_{\mathrm{core}} + H_{\mathrm{gap}} L_{\mathrm{gap}}\,$

$NI = B(\frac{L_{\mathrm{core}}}{\mu} + \frac{L_{\mathrm{gap}}}{\mu_0}) \qquad \qquad \qquad \qquad (1) \,$

where $\mu = B/H\,$

$\mu_0 = 4 \pi (10^{-7}) \ \mathrm{N} \cdot \mathrm{A}^{-2}$ is the permeability of free space (or air).

This is a nonlinear equation, because the permeability of the core, μ, is a function of the magnetic field. For an exact solution, the value of μ at the B value used must be obtained from the core material hysteresis curve. If B is unknown, the equation must be solved by numerical methods. However, if the magnetomotive force is well above saturation, so the core material is in saturation, the magnetic field won't vary much with changes in NI anyway. For a closed magnetic circuit (no air gap) most core materials saturate at a magnetomotive force of roughly 800 ampere-turns per meter of flux path.

For most core materials, 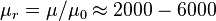$\mu_r = \mu / \mu_0 \approx 2000 - 6000\,$ .^[11] So in equation (1) above, the second term dominates. Therefore, in magnetic circuits with an air gap, the behavior of the magnet depends strongly on the length of the air gap, and the length of the flux path in the core doesn't matter much.

[edit] Force exerted by magnetic field

When none of the magnetic field bypasses any sections of the core (no flux leakage), the force exerted by an electromagnet on the core material is:

$F = \frac{B^2 A}{2 \mu_0} \qquad \qquad \qquad \qquad \qquad \qquad (2) \,$

The 1.6 T limit on the field mentioned above sets a limit on the maximum force per unit core area, or pressure, an iron-core electromagnet can exert; roughly:

$\frac{F}{A} \approx 1000\ \mathrm{kPa} = 145\ \mathrm{lbf} \cdot \mathrm{in}^{-2}\,$

Given a core geometry, the B field needed for a given force can be calculated from (2); if it comes out to much more than 1.6 T, a larger core must be used.

[edit] Closed magnetic circuit

Cross section of 1914 lifting electromagnet like that in above photo, showing cylindrical construction. The windings (C) are flat copper strips to withstand the Lorentz force of the magnetic field. The core is formed by the thick iron housing (D) that wraps around the windings.

For a closed magnetic circuit (no air gap), such as would be found in an electromagnet lifting a piece of iron, equation (1) becomes:

$B = \frac{NI\mu}{L} \qquad \qquad \qquad \qquad \qquad \qquad (3) \,$

Substituting into (2), the force is:

$F = \frac{\mu^2 N^2 I^2 A}{2\mu_0 L^2} \qquad \qquad \qquad \qquad \qquad (4) \,$

It can be seen that to maximize the force, a short flux path with a wide cross sectional area is preferred. To achieve this, in applications like lifting magnets (see photo above) and loudspeakers a flat cylindrical design is often used. The winding is wrapped around a short wide cylindrical core that forms one pole, and a thick metal housing that wraps around the outside of the windings forms the other part of the magnetic circuit, bringing the magnetic field to the front to form the other pole.

[edit] Force between electromagnets

The above methods are inapplicable when most of the magnetic field path is outside the core. For electromagnets (or permanent magnets) with well defined 'poles' where the field lines emerge from the core, the force between two electromagnets can be found using the 'Gilbert model' which assumes the magnetic field is produced by fictitious 'magnetic charges' on the surface of the poles, with pole strength m and units of Ampere-turn meter. Magnetic pole strength of electromagnets can be found from:

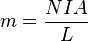
$m = \frac{NIA}{L}$

The force between two poles is:

$F = \frac{\mu_0 m_1 m_2}{4\pi r^2}$

This model doesn't give the correct magnetic field inside the core, and thus gives incorrect results if the pole of one magnet gets too close to another magnet.

[edit] High field electromagnets

[edit] Superconducting electromagnets

Main article: Superconducting magnet

When a magnetic field higher than the ferromagnetic limit of 1.6 T is needed, superconducting electromagnets can be used. Instead of using ferromagnetic materials, these use superconducting windings cooled with liquid helium, which conduct current without electrical resistance. These allow enormous currents to flow, which generate intense magnetic fields. Superconducting magnets are limited by the field strength at which the winding material ceases to be superconducting. Current designs are limited to 10–20 T, with the record of 26.8 T.^[12] The necessary refrigeration equipment and cryostat make them much more expensive than ordinary electromagnets. However, in high power applications this can be offset by lower operating costs, since after startup no power is required for the windings, since no energy is lost to ohmic heating. They are used in particle accelerators, MRI machines, and research.

[edit] Bitter electromagnets

Since both iron-core and superconducting electromagnets have limits to the field they can produce, the highest manmade magnetic fields have been generated by air-core nonsuperconducting electromagnets of a design invented by Francis Bitter in 1933, called Bitter electromagnets.^[13] These consist of a solenoid made of a stack of conducting disks, arranged so that the current moves in a helical path through them. This design has the mechanical strength to withstand the extreme Lorentz forces of the field, which increase with B². The disks are pierced with holes through which cooling water passes to carry away the heat caused by the high current. The highest continuous field achieved with a resistive magnet is currently (2008) 35 T.^[12] The highest continuous magnetic field, 45 T, was achieved with a hybrid device consisting of a Bitter magnet inside a superconducting magnet.

[edit] Exploding electromagnets

The factor limiting the strength of electromagnets is the inability to dissipate the enormous waste heat, so higher fields, up to 90 T, have been obtained from resistive magnets by pulsing them. The highest magnetic fields of all have been created by detonating explosives around a pulsed electromagnet as it is turned on. The implosion compresses the magnetic field to values of around 1000 T for a few microseconds.

[edit] Uses of electromagnets

Electromagnets are widely used in many electric devices, including:

Motors and generators
Relays, including reed relays originally used in telephone exchanges
Electric bells
Loudspeakers
Magnetic recording and data storage equipment: tape recorders, VCRs, hard disks
Particle accelerators
Magnetic locks
Magnetic separation of materials
Industrial lifting magnets

[edit] Definition of terms

$A\,$	square meter	cross section area of core
$B\,$	tesla	Magnetic field
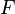$F\,$	newton	Force exerted by magnetic field
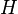$H\,$	ampere per meter	Magnetizing field
$I\,$	ampere	Current in the winding wire
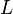$L\,$	meter	Total length of the magnetic field path $L_{\mathrm{core}}+L_{\mathrm{gap}}\,$
$L_{\mathrm{core}}\,$	meter	Length of the magnetic field path in the core material
$L_{\mathrm{gap}}\,$	meter	Length of the magnetic field path air gap
$m_1, m_2\,$	ampere meter	Pole strength of the electromagnets
$\mu\,$	newton per square ampere	Permeability of the electromagnet core material
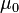$\mu_0\,$	newton per square ampere	Permeability of free space (or air) = 4π(10^-7)
$\mu_r\,$	-	Relative permeability of the electromagnet core material
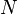$N\,$	-	Number of turns of wire on the electromagnet
$r\,$	meter	Distance between the poles of two electromagnets