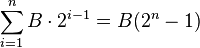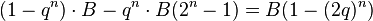Martingale (betting system)
From Wikipedia, the free encyclopedia
| This article does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (November 2006) |
- A separate article treats the topic of Martingale (probability theory).
Originally, martingale referred to a class of betting strategies popular in 18th-century France. The name is not eponymous and there is no Monsieur Martingale. The simplest of these strategies was designed for a game in which the gambler wins his stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double his bet after every loss, so that the first win would recover all previous losses plus win a profit equal to the original stake. Since a gambler with infinite wealth will with probability 1 eventually flip heads, the Martingale betting strategy was seen as a sure thing by those who practised it. Of course, none of these practitioners in fact possessed infinite wealth, and the exponential growth of the bets would eventually bankrupt those who choose to use the Martingale. It is widely believed that casinos instituted betting limits specifically to stop Martingale players, but in reality the assumptions behind the strategy are unsound. Players using the Martingale system do not have any long term mathematical advantage over any other betting system or even randomly placed bets.
Contents |
[edit] Effect of variance
As with any betting system, it is possible to have variance from the expected negative return by temporarily avoiding the inevitable losing streak. Furthermore, a straight string of losses is the only sequence of outcomes that results in a loss of money, so even when a player has lost the majority of their bets, they can still be ahead over-all, since they always win 1 unit when a bet wins, regardless of how many previous losses.[1]
[edit] Intuitive analysis
Since expectation is linear, the expected value of a series of bets is just the sum of the expected value of each bet. Since in such games of chance the bets are independent, the expectation of all bets is going to be the same, regardless of whether you previously won or lost. In most casino games, the expected value of any individual bet is negative, so the sum of lots of negative numbers is also always going to be negative.
[edit] Mathematical analysis
The impossibility of winning over the long run, given a limit of the size of bets or a limit in the size of one's bankroll or line of credit, is proven by the optional stopping theorem.
[edit] Mathematical analysis of a single round
Let one round be defined as a sequence of consecutive losses followed by a win, or consecutive losses resulting in bankruptcy of the gambler. After a win, the gambler "resets" and is considered to have started a new round. A continuous sequence of martingale bets can thus be partitioned into a sequence of independent rounds. We will analyze the expected value of one round.
Let q be the probability of losing (e.g. for roulette it is 20/38). Let B be the amount of the commencing bet. Let n be the finite number of bets you can afford to lose.
The probability that you lose all n bets is qn. When you lose all your bets, the amount of money you lose is
The probability that you do not lose all n bets is 1 − qn. If you do not lose all n bets, you win B amount of money (the initial bet amount). So the expected profit per round is
Whenever q > 1/2, the expression 1 − (2q)n < 0 for all n > 0. That means for any game where it is more likely to lose than to win (e.g. all chance gambling games), you are expected to lose money on average per round. Furthermore, the more times you are able to afford to bet, the more you will lose.
As an example, suppose you have 6,300 available to bet. You bet 100 on the first spin. If you lose, you bet 200 on the second spin, then 400 on the third, 800 on the fourth, 1,600 on the fifth, and 3,200 on the sixth.
If you win 100 on the first spin, you make 100, and the martingale starts over.
If you lose 100 on the first spin and win 200 on the second spin, you make a net profit of 100 at which point the martingale would start over.
If you lose on the first five spins, you lose a total of 3,100 (3,100 = 100 + 200 + 400 + 800 + 1,600). On the sixth spin you bet 3,200. If you win, you again make a profit of 100.
If you lose on the first six spins, you have lost a total of 6,300 and with only 6,300 available, you do not have enough money to double your previous bet. At this point the martingale can not be continued.
In this example the probability of losing 6,300 and being unable to continue the martingale is equal to the probability of losing 6 times or (20/38)^6 = 2.1256%. The probability of winning 100 is equal to 1 minus the probability of losing 6 times or 1 - (20/38)^6 = 97.8744%.
The expected value of winning is + (100*.978744) = 97.8744 . The expected value of losing is + (-6,300*.021256)= -133.9128 . The expected value of the Martingale strategy is that you will lose or -36.034 .
[edit] Alternate Mathematical analysis of a single round
The previous analysis calculates expected value, but we could restate the problem in terms of what is the probability that one can play a casino game using the Martingale strategy, and avoid the losing streak long enough to double the bankroll.
Using the same definitions above, we could restate the same problem as what is the likelihood of losing 6 roulette spins in a row assuming we are betting red/black or even/odd. Many gamblers believe that the odds of losing 6 in a row are remote, and with a patience of adhering to the strategy they will slowly increase their bankroll.
In reality, the odds of a streak of 6 losses in a row are much higher than the most people intuitively believe. Psychological studies have shown that since people know that the odds of losing 6 times in a row out of 6 plays are very low, they incorrectly assume that out of a longer string of plays the odds are also very low. When people are asked to falsify data representing 200 coin tosses, they almost always do not add streaks of more than 5 because they believe that these streaks are very unlikely[citation needed]. This intuitive belief is sometimes referred to as the representativeness heuristic.
The odds of losing at roulette are q=20/38=52.56316%. If you play a total of 6 spins, the odds of losing 6 times are q^6=2.1256% as stated before. However if you play more and more spins, the odds of losing 6 times in a row begin to increase rapidly.
- In 68 spins there is a 50.3% chance that you will lose 6 times in a row at roulette.
- In 150 spins there is a 80.6% chance that you will lose 6 times in a row at roulette.
- In 250 spins there is a 95.3% chance that you will lose 6 times in a row at roulette.
To double the initial bankroll of 6,300 with initial bets of 100 would require a minimum of 63 spins (in the unlikely event you win every time), and a maximum of 378 spins ( in the equally unlikely event that you win every single round on the sixth spin). The required number will more than likely be more than 150 spins. So many gamblers believe that they can play the Martingale strategy with very little chance of failure long enough to double their bankroll. However, the odds of losing 6 in a row are 80.6% out of 150 spins.
We can replace the roulette game in the analysis with either the pass line at craps where the odds of losing are lower q=251/244=50.7071% or a coin toss game where the odds of losing are 50.0%. We should note that games like coin toss with no house edge are not played in a commercial casino and thus represent a limiting case.
- In 150 turns there is a 73.5% chance that you will lose 6 times in a row on the pass line.
- In 150 turns there is a 70.7% chance that you will lose 6 times in a row at coin tossing.
In larger casinos the maximum table limit is higher, so that you can double 7,8 or 9 times without exceeding the limit. However, in order to end up with twice your initial bankroll you must play even longer. The calculations produce the same results. The probabilities are overwhelming that you will reach the bust streak before you can even double your bankroll.
The conclusion is that players using Martingale strategy pose no threat to a casino. The odds are very high that the player will go bust before he is able to even double his money.
Table limits are not designed to prevent players from using Martingale strategy. They exist so that the casino is not gambling more money than they can afford to lose. Statistics as of January 2009 show that the 29 roulette wheels in Downtown gaming Las Vegas average a win amount of $1,114 per day for the last year. Most casinos have a $500 dollar table limit so that so that they are not risking too much money on a few spins. A casino is a business and, like any other business, it has to worry about cash flow. Casinos are required to keep enough cash on hand to pay off a reasonable expectation of a gambler's windfall. A small casino with a pit that normally takes in $12–$15 thousand a day doesn't want to keep enough cash on hand to pay off a $10,000 bet that hits 36:1 on roulette. A major casino on the strip earns over $3000 per day on a roulette game and can have over 20 roulette games. They can risk no-limit tables. They would welcome a Martingale strategy player.
[edit] Anti-martingale
In a classic martingale betting style, gamblers will increase their bets after each loss in hopes that an eventual win will recover all previous losses. The anti-martingale approach instead increases bets after wins, while reducing them after a loss. The perception is that in this manner the gambler will benefit from a winning streak or a "hot hand", while reducing losses while "cold" or otherwise having a losing streak.
[edit] Betting Strategy vs. Card Counting
In a true random memoryless game any betting strategy (like Martingale) can't improve the expected winnings. The odds of winning are entirely governed by the expected calculation of house edge. Classic casino games such as European Roulette have an expected loss of 19/37 for each play, American roulette is 20/38, Pass line bet in craps is 251/459, and the Don't pass Line is 1031/1980. Slot machines also have an expectation but it is legally permitted to be kept secret from the player. The acronym for the table that shows the probability for different outcomes for a given machine is its PARS, which is an acronym for Paytable and Reel Strips.
Card counting has a superficial resemblance to betting strategies because the initial wager is increased and decreased. However a deck of cards is not a random memoryless game. The strategy is based on the reality that a deck with many Aces and 10 value cards remaining is very likely to produce a blackjack (or natural). The blackjack is just as likely to go to the dealer as the player. However, the player gets paid a bonus for getting a blackjack (traditionally 50%) while the dealer only wins the original stake. If the player uses a strategy to estimate that the remaining cards in the deck are rich in 10's and Aces he increases his bet to take advantage of the increased possibility of a blackjack. The traditional game previous to 1960 used a single deck of cards and was dealt nearly to the bottom of the deck. It was possible to invent strategies that could easily be taught to make good estimates of the number of Aces and 10's remaining in the deck. Card counting is not cheating because the player does not use subterfuge to know the outcome, he merely knows that the probabilities have changed to be more in his favor. So an effective card counter must have an extremely large bankroll to cover the times when his initial bet is large, but the dealer still wins. Casinos have implemented multiple rule changes that make this estimation much more difficult. The easiest one is that the pit boss does not permit a wide range of initial wagers and invites the player to change to a different game if he insists on maintaining this behaviour.
[edit] In popular culture
In the CSI: Las Vegas episode "XX", a character borrows thousands of dollars to test out a brilliant gambling strategy, which turns out to be the Martingale system.
[edit] Notes and references
- ^ http://www.blackjackincolor.com/useless4.htm Martingale Long Term vs. Short Term Charts