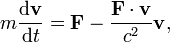Newton's laws of motion

From Wikipedia, the free encyclopedia

Jump to: navigation, search
For other uses, see Laws of motion.
Newton's First and Second laws, in Latin, from the original 1687 edition of the Principia Mathematica.
Classical mechanics
History of ...
Formulations
Newtonian mechanics
Lagrangian mechanics
Hamiltonian mechanics
This box: view • talk • edit

Newton's laws of motion are three physical laws that form the basis for classical mechanics, directly relating the forces acting on a body to the motion of the body. They were first compiled by Sir Isaac Newton in his work Philosophiæ Naturalis Principia Mathematica, first published on July 5, 1687.[1] Newton used them to explain and investigate the motion of many physical objects and systems.[2] For example, in the third volume of the text, Newton showed that these laws of motion, combined with his law of universal gravitation, explained Kepler's laws of planetary motion.

First law
There exists a set of inertial reference frames relative to which all particles with no net force acting on them will move without change in their velocity. This law is often simplified as "A body persists its state of rest or of uniform motion unless acted upon by an external unbalanced force." Newton's first law is often referred to as the law of inertia. So in other words "every object in motion will stay in motion until acted upon by an outside force."
Second law
Observed from an inertial reference frame, the net force on a particle of constant mass is proportional to the time rate of change of its linear momentum: F = d(mv)/dt. This law is often stated as, "Force equals mass times acceleration (F = ma)": the net force on an object is equal to the mass of the object multiplied by its acceleration.
Third law
Whenever a particle A exerts a force on another particle B, B simultaneously exerts a force on A with the same magnitude in the opposite direction. The strong form of the law further postulates that these two forces act along the same line. This law is often simplified into the sentence, "To every action there is an equal and opposite reaction."

In the given interpretation mass, acceleration, momentum, and (most importantly) force are assumed to be externally defined quantities. This is the most common, but not the only interpretation: one can consider the laws to be a definition of these quantities. Notice that the second law only holds when the observation is made from an inertial reference frame, and since an inertial reference frame is defined by the first law, asking a proof of the first law from the second law is a logical fallacy. At speeds approaching the speed of light the effects of special relativity must be taken into account.[3]


Contents

[edit] Newton's first law: law of inertia

Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare. Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed. [4]

Newton's first law is also called the law of inertia. In a simplified form, it states that if the vector sum of all forces (also known as the net force) acting on an object is zero, then the state of motion of the object does not change. In particular: Newton's first law: An object at rest remains at rest and an object in motion will remain in motion unless acted on by an unbalanced force.

  • An object that is not moving will not move until a net force acts upon it.
  • An object that is moving will not change its velocity (accelerate) until a net force acts upon it.

The first point needs no comment, but the second seems to violate everyday experience. A hockey puck sliding along a table doesn't move forever; rather, it slows and eventually comes to a stop. According to Newton's laws, though, the hockey puck does not stop of its own accord, but because of a force applied in the opposite direction to the direction of motion. That force is easily identified as a frictional force between the table and the puck. In the absence of such a force, as approximated by an air hockey table or ice rink, the puck's motion would not slow.

There are no perfect demonstrations of the law, as friction usually causes a force to act on a moving body, and even in outer space gravitational forces act and cannot be shielded against, but the law serves to emphasize the elementary causes of changes in an object's state of motion.

The above treatment of Newton's first law is an over-simplification, though. A more sophisticated approach to the law of inertia is given by:

There is a class of frames of reference (called inertial frames) relative to which the motion of a particle not subject to forces is a straight line. [5]

Newton placed the law of inertia first to establish frames of reference for which the other laws are applicable (see Gailili & Tseitlin[6], or Woodhouse[5]). Such frames are called inertial frames.

To understand why the laws are restricted to inertial frames, consider a ball at rest within an accelerating body: an airplane on a runway will suffice for this example. From the perspective of anyone within the airplane (that is, from the airplane's frame of reference when put in technical terms) the ball will appear to move backwards as the plane accelerates forwards (the same feeling as being pushed back into your seat as the plane accelerates). This motion appears to contradict Newton's second law as, from the point of view of the passengers, there appears to be no force acting on the ball that would cause it to move. The reason why there is in fact no contradiction to the second law is because Newton's second law (without modification) is not applicable in this situation: Newton's first law does not apply because the stationary ball does not remain stationary. Thus, it is important to establish whether the various laws are applicable or not, inasmuch as they are not applicable in all situations.[7]

[edit] History of the Law of Inertia

Newton's first law is a restatement of what Galileo had already described and Newton gave credit to Galileo. It differs from Aristotle's view that all objects have a natural place in the universe. Aristotle believed that heavy objects like rocks wanted to be at rest on the Earth and that light objects like smoke wanted to be at rest in the sky and the stars wanted to remain in the heavens. However, a key difference between Galileo's idea and Aristotle's is that Galileo realized that force acting on a body determines acceleration, not velocity. This insight leads to Newton's First Law—no force means no acceleration, and hence the body will maintain its velocity.

The law of inertia apparently occurred to several different natural philosophers and scientists independently. The inertia of motion was described in the 3rd century BC by the Chinese philosopher Mo Tzu, and in the 11th century by the Muslim scientists, Alhazen[8] and Avicenna.[9] The 17th century philosopher René Descartes also formulated the law, although he did not perform any experiments to confirm it.

[edit] Newton's second law

192448main 018 force equals mass time.ogg
Explanation of Newton's second law by NASA employee.

Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur. The change of momentum of a body is proportional to the impulse impressed on the body, and happens along the straight line on which that impulse is impressed.

In Motte's 1729 translation (from Newton's Latin), the second law of motion reads:[10]

LAW II: The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed. — If a force generates a motion, a double force will generate double the motion, a triple force triple the motion, whether that force be impressed altogether and at once, or gradually and successively. And this motion (being always directed the same way with the generating force), if the body moved before, is added to or subtracted from the former motion, according as they directly conspire with or are directly contrary to each other; or obliquely joined, when they are oblique, so as to produce a new motion compounded from the determination of both.

Using modern symbolic notation, Newton's second law can be written as a vector differential equation:

\mathbf F_{\text{net}} = {\mathrm{d}(m \mathbf v) \over \mathrm{d}t} = m \ \frac{d \mathbf v}{dt}

where F is the force vector, m is the mass of the body, v is the velocity vector and t is time.

The product of the mass and velocity is the momentum of the object (which Newton himself called "quantity of motion"). Therefore, this equation expresses the physical relationship between force and momentum for systems of constant relativistic mass. The equation implies that, under zero net force, the momentum of a system is constant; however, any mass that enters or leaves the system will cause a change in system momentum that is not the result of an external force. This equation does not hold in such cases. See open systems.

It should be noted that, as is consistent with the law of inertia, the time derivative of the momentum is non-zero when the momentum changes direction, even if there is no change in its magnitude. See time derivative.[11]

Since the mass of the system is constant, this differential equation can be rewritten in its simpler and more familiar form:

\mathbf F = m \mathbf a

where

\mathbf a = \frac{\mathrm{d} \mathbf v}{\mathrm{d}t}

is the acceleration.

A verbal equivalent of this is "the acceleration of an object is proportional to the force applied, and inversely proportional to the mass of the object". In general, at slow speeds (slow relative to the speed of light), the relationship between momentum and velocity is approximately linear. Nearly all speeds within the human experience fall within this category. At higher speeds, however, this approximation becomes increasingly inaccurate and the theory of special relativity must be applied.

[edit] Impulse

The term impulse is closely related to the second law, and historically speaking is closer to the original meaning of the law.[12]The meaning of an impulse is as follows:[13][14]

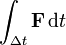An impulse occurs when a force F acts over an interval of time Δt and is given by \int_{\Delta t} \mathbf F \,\mathrm{d}t .

The words motive force were used by Newton to describe "impulse" and motion to describe momentum; consequently, a historically closer reading of the second law describes the relation between impulse and change of momentum. That is, a mathematical rendering of the original wording resembles a finite difference version of the second law, such as

\mathbf{I} = \Delta\mathbf{p} = m\Delta\mathbf{v}

where I is the impulse, Δp is the change in momentum, m is the mass, and Δv is the change in velocity.

The analysis of collisions and impacts uses the impulse concept.[15]

[edit] Relativity

Taking special relativity into consideration, the law of resultant force can be put in terms of acceleration as follows:[16]

\begin{align} \mathbf F &= \frac {\mathrm{d} \mathbf {p} }{\mathrm{d} t} = \frac {\mathrm{d} (m \mathbf {v}) }{\mathrm{d} t} \\ &= m \frac {\mathrm{d}\mathbf{v}} {\mathrm{d}t} + \frac {\mathrm{d} m }{\mathrm{d} t}\mathbf {v} \\ &= m \frac {\mathrm{d}\mathbf{v}} {\mathrm{d}t} + \frac{1}{c^2} \frac {\mathrm{d} E }{\mathrm{d} t}\mathbf{v} \\ &= m \frac {\mathrm{d}\mathbf{v}} {\mathrm{d}t} + \frac { \mathbf{F} \cdot \mathbf{v} }{c^2}\mathbf{v} \end{align}

where the famous result for the energy E = mc2 is used (where c is the speed of light in free space). Note that this is an approximate formula, where γ in the exact expression of relativistic energy, E = γmc2, is approximately one. The relation

\frac {\mathrm{d}E} {\mathrm{d}t} = \mathbf F \cdot \mathbf v

describes the work done by the force per unit time. Here F·v is the vector dot product.

This equation can be rearranged to form the modified force law

m \frac {\mathrm{d}\mathbf{v}}{\mathrm{d}t} = \mathbf F - \frac {\mathbf F \cdot \mathbf v}{c^2} \mathbf v \text{,}

which shows that although the change of momentum is in the direction of the force, in general the acceleration of the mass is not in the direction of the force. However, when the speed of the moving body is much lower than the speed of light, the equation above reduces to the familiar F=ma.

[edit] Open systems

So-called variable mass systems that are not closed systems, like a rocket burning fuel and ejecting spent gases, can not be directly treated by making mass a function of time in the second law.[17][18] The reasoning, given in An Introduction to Mechanics by Kleppner and Kolenkow and other modern texts, is that Newton's second law applies fundamentally to particles. In classical mechanics, particles by definition have constant mass. In case of well-defined systems of particles, Newton's law can be extended by summing over all the particles in the system. In this case, we have to refer all vectors to the center of mass. Applying the second law to extended objects implicitly assumes the object to be a well-defined collection of particles. However, 'variable mass' systems like a rocket or a leaking bucket do not consist of a set number of particles. They are not well-defined systems. Therefore Newton's second law can not be applied to them directly. The naïve application of F = dp/dt will usually result in wrong answers in such cases. However, applying the conservation of momentum to a complete system (such as a rocket and fuel, or a bucket and leaked water) will give unambiguously correct answers.

The term "complete system" in the last sentence refers to a larger, constant mass system that accounts for all the particles. This effectively means that F = dp/dt is true only for constant mass systems. Expressed in the form F = ma, however, it correctly describes the motion of any particle or system regardless of varying mass, provided that the resultant force F is taken to include the thrust of any mass entering or leaving the system.

[edit] Newton's third law: law of reciprocal actions

Lex III: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi. For a force there is always an equal and opposite reaction: or the forces of two bodies on each other are always equal and are directed in opposite directions.

Newton's third law. The skaters' forces on each other are equal in magnitude, but act in opposite directions.
192449main 019 law of action.ogg
Explanation of Newton's third law by NASA employee.

A more direct[clarification needed] translation is:

LAW III: To every action there is always opposed an equal reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts. — Whatever draws or presses another is as much drawn or pressed by that other. If you press a stone with your finger, the finger is also pressed by the stone. If a horse draws a stone tied to a rope, the horse (if I may so say) will be equally drawn back towards the stone: for the distended rope, by the same endeavour to relax or unbend itself, will draw the horse as much towards the stone, as it does the stone towards the horse, and will obstruct the progress of the one as much as it advances that of the other. If a body impinges upon another, and by its force changes the motion of the other, that body also (because of the equality of the mutual pressure) will undergo an equal change, in its own motion, toward the contrary part. The changes made by these actions are equal, not in the velocities but in the motions of the bodies; that is to say, if the bodies are not hindered by any other impediments. For, as the motions are equally changed, the changes of the velocities made toward contrary parts are reciprocally proportional to the bodies. This law takes place also in attractions, as will be proved in the next scholium.

In the above, as usual, motion is Newton's name for momentum, hence his careful distinction between motion and velocity.

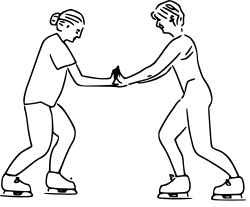
The Third Law means that all forces are interactions, and thus that there is no such thing as a unidirectional force. If body A exerts a force on body B, simultaneously, body B exerts a force of the same magnitude body A, both forces acting along the same line. As shown in the diagram opposite, the skaters' forces on each other are equal in magnitude, but act in opposite directions. Although the forces are equal, the accelerations are not: the less massive skater will have a greater acceleration due to Newton's second law. It is important to note that the action and reaction act on different objects and do not cancel each other out. The two forces in Newton's third law are of the same type (e.g., if the road exerts a forward frictional force on an accelerating car's tires, then it is also a frictional force that Newton's third law predicts for the tires pushing backward on the road).

Newton used the third law to derive the law of conservation of momentum;[19] however from a deeper perspective, conservation of momentum is the more fundamental idea (derived via Noether's theorem from Galilean invariance), and holds in cases where Newton's third law appears to fail, for instance when force fields as well as particles carry momentum, and in quantum mechanics.

[edit] Importance and range of validity

Newton's laws were verified by experiment and observation for over 200 years, and they are excellent approximations at the scales and speeds of everyday life. Newton's laws of motion, together with his law of universal gravitation and the mathematical techniques of calculus, provided for the first time a unified quantitative explanation for a wide range of physical phenomena.

These three laws hold to a good approximation for macroscopic objects under everyday conditions. However, Newton's laws (combined with Universal Gravitation and Classical Electrodynamics) are inappropriate for use in certain circumstances, most notably at very small scales, very high speeds (in special relativity, the Lorentz factor must be included in the expression for momentum along with rest mass and velocity) or very strong gravitational fields. Therefore, the laws cannot be used to explain phenomena such as conduction of electricity in a semiconductor, optical properties of substances, errors in non-relativistically corrected GPS systems and superconductivity. Explanation of these phenomena requires more sophisticated physical theory, including General Relativity and Relativistic Quantum Mechanics.

In quantum mechanics concepts such as force, momentum, and position are defined by linear operators that operate on the quantum state; at speeds that are much lower than the speed of light, Newton's laws are just as exact for these operators as they are for classical objects. At speeds comparable to the speed of light, the second law holds in the original form F = dp/dt, which says that the force is the derivative of the momentum of the object with respect to time, but some of the newer versions of the second law (such as the constant mass approximation above) do not hold at relativistic velocities.

[edit] Relationship to the conservation laws

In modern physics, the laws of conservation of momentum, energy, and angular momentum are of more general validity than Newton's laws, since they apply to both light and matter, and to both classical and non-classical physics.

This can be stated simply, "Momentum, energy and angular momentum cannot be created or destroyed."

Because force is the time derivative of momentum, the concept of force is redundant and subordinate to the conservation of momentum, and is not used in fundamental theories (e.g. quantum mechanics, quantum electrodynamics, general relativity, etc.). The standard model explains in detail how the three fundamental forces known as gauge forces originate out of exchange by virtual particles. Other forces such as gravity and fermionic degeneracy pressure also arise from the momentum conservation. Indeed, the conservation of 4-momentum in inertial motion via curved space-time results in what we call gravitational force in general relativity theory. Application of space derivative (which is a momentum operator in quantum mechanics) to overlaping wave functions of pair of fermions (particles with semi-integer spin) results in shifts of maxima of compound wavefunction away from each other, which is observable as "repulsion" of fermions.

Newton stated the third law within a world-view that assumed instantaneous action at a distance between material particles. However, he was prepared for philosophical criticism of this action at a distance, and it was in this context that he stated the famous phrase "I feign no hypotheses". In modern physics, action at a distance has been completely eliminated, except for subtle effects involving quantum entanglement. However in modern engineering in all practical applications involving the motion of vehicles and satellites, the concept of action at a distance is used extensively.

Conservation of energy was discovered nearly two centuries after Newton's lifetime, the long delay occurring because of the difficulty in understanding the role of microscopic and invisible forms of energy such as heat and infra-red light.

[edit] See also

[edit] References and notes

  1. ^ See the Principia on line at Andrew Motte Translation
  2. ^ Andrew Motte translation of Newton's Principia (1687) Axioms or Laws of Motion
  3. ^ In the second law, m must be treated as the relatistic mass, producing the relativistic expression for momentum, and the third law must be modified to allow for the finite signal propagation speed between distant interacting particles.
  4. ^ Isaac Newton, The Principia, A new translation by I.B. Cohen and A. Whitman, University of California press, Berkeley 1999.
  5. ^ a b NMJ Woodhouse (2003). Special relativity. London/Berlin: Springer. p. 6. ISBN 1-85233-426-6. http://books.google.com/books?id=ggPXQAeeRLgC&printsec=frontcover&dq=isbn=1852334266#PPA6,M1. 
  6. ^ Galili, I. & Tseitlin, M. (2003), "Newton's first law: text, translations, interpretations, and physics education.", Science and Education 12 (1): 45–73 
  7. ^ On a more technical note, although Newton's laws are not applicable on non-inertial frames of reference, such as the accelerating airplane, they can be made to do so with the introduction of a "fictitious force" acting on the entire system: basically, by introducing a force that quantifies the anomalous motion of objects within that system (such as the ball moving without an apparent influence in the example above
  8. ^ Abdus Salam (1984), "Islam and Science". In C. H. Lai (1987), Ideals and Realities: Selected Essays of Abdus Salam, 2nd ed., World Scientific, Singapore, p. 179-213.
  9. ^ Fernando Espinoza (2005). "An analysis of the historical development of ideas about motion and its implications for teaching", Physics Education 40 (2), p. 141.
  10. ^ According to Maxwell in Matter and Motion, Newton meant by motion "the quantity of matter moved as well as the rate at which it travels" and by impressed force he meant "the time during which the force acts as well as the intensity of the force". See Harman and Shapiro,cited below.
  11. ^ The use of algebraic expressions became popular during the 18th century, after Newton's death, while vector notation dates to the late 19th century. The Principia expresses mathematical theorems in words and consistently uses geometrical rather than algebraic proofs.
  12. ^ I Bernard Cohen (Peter M. Harman & Alan E. Shapiro, Eds) (2002). The investigation of difficult things : essays on Newton and the history of the exact sciences in honour of D.T. Whiteside. Cambridge UK: Cambridge University Press. p. 353. ISBN 052189266X. http://books.google.com/books?id=oYZ-0PUrjBcC&pg=PA353&dq=impulse+momentum+%22rate+of+change%22+-angular+date:2000-2009&lr=&as_brr=0&sig=xM_5Q-nrbPkLLKcXAAbmogvVTcU. 
  13. ^ Hannah, J, Hillier, M J, Applied Mechanics, p221, Pitman Paperbacks, 1971
  14. ^ Raymond A. Serway, Jerry S. Faughn (2006). College Physics. Pacific Grove CA: Thompson-Brooks/Cole. p. 161. ISBN 0534997244. http://books.google.com/books?id=wDKD4IggBJ4C&pg=PA247&dq=impulse+momentum+%22rate+of+change%22&lr=&as_brr=0&sig=Up5LC1E784npQuR2lyDde6SetoQ#PPA161,M1. 
  15. ^ WJ Stronge (2004). Impact mechanics. Cambridge UK: Cambridge University Press. p. 12 ff. ISBN 0521602890. http://books.google.com/books?id=nHgcS0bfZ28C&pg=PA12&dq=impulse+momentum+%22rate+of+change%22+-angular+date:2000-2009&lr=&as_brr=0&sig=YVDmNVMz38AubS-5lvRADvD2n6k. 
  16. ^ C Møller (1976). The Theory of Relativity (Second Edition ed.). Oxford UK: Oxford University Press. p. 70-75. ISBN 019560539X. http://worldcat.org/oclc/220221617&referer=brief_results. 
  17. ^ Halliday; Resnick. Physics. 1. pp. 199. "It is important to note that we cannot derive a general expression for Newton's second law for variable mass systems by treating the mass in F = dP/dt = d(Mv) as a variable. [...] We can use F = dP/dt to analyze variable mass systems only if we apply it to an entire system of constant mass having parts among which there is an interchange of mass."  [Emphasis as in the original]
  18. ^ Kleppner; Kolenkow. An Introduction to Mechanics. pp. 133–134. "Recall that F = dP/dt was established for a system composed of a certain set of particles...it is essential to deal with the same set of particles throughout the time interval...Consequently, the mass of the system can not change during the time of interest." 
  19. ^ Newton, Principia, Corollary III to the laws of motion

[edit] Further reading

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Newton%27s_laws_of_motion"
Personal tools