Euclidean distance
From Wikipedia, the free encyclopedia
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, which can be proven by repeated application of the Pythagorean theorem. By using this formula as distance, Euclidean space becomes a metric space (even a Hilbert space). The associated norm is called the Euclidean norm.
Older literature refers to this metric as Pythagorean metric. The technique has been rediscovered numerous times throughout history, as it is a logical extension of the Pythagorean theorem.
Contents |
[edit] Definition
The Euclidean distance between points  and
and 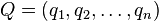 , in Euclidean n-space, is defined as:
, in Euclidean n-space, is defined as:
[edit] One-dimensional distance
For two 1D points, 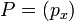 and
and 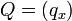 , the distance is computed as
, the distance is computed as
The absolute value signs are used since distance is normally considered to be an unsigned scalar value.
In one dimension, there is a single homogeneous, translation-invariant metric (in other words, a distance that is induced by a norm), up to a scale factor of length, which is the Euclidean distance. In higher dimensions there are other possible norms.
[edit] Two-dimensional distance
For two 2D points, 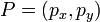 and
and  , the distance is computed as:
, the distance is computed as:
Alternatively, expressed in polar coordinates, using  and
and 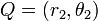 , the distance can be computed as:
, the distance can be computed as:
[edit] Three-dimensional distance
For two 3D points,  and
and  , the distance is computed as
, the distance is computed as
[edit] N-dimensional distance
For two N-D points, 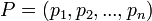 and
and  , the distance is computed as
, the distance is computed as







