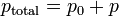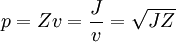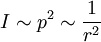Sound pressure

Sound measurements
	Sound pressure p
	Particle velocity v
	Particle velocity level (SVL)
	(Sound velocity level)
	Particle displacement ξ
	Sound intensity I
	Sound intensity level (SIL)
	Sound power Pac
	Sound power level (SWL)
	Sound energy density E
	Sound energy flux q
	Surface S
	Acoustic impedance Z
	Speed of sound c v • d • e

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Sound pressure is the local pressure deviation from the ambient (average, or equilibrium) pressure caused by a sound wave. Sound pressure can be measured using a microphone in air and a hydrophone in water. The SI unit for sound pressure is the pascal (symbol: Pa). The instantaneous sound pressure is the deviation from the local ambient pressure p₀ caused by a sound wave at a given location and given instant in time. The effective sound pressure is the root mean square of the instantaneous sound pressure over a given interval of time (or space). In a sound wave, the complementary variable to sound pressure is the acoustic particle velocity. For small amplitudes, sound pressure and particle velocity are linearly related and their ratio is the acoustic impedance. The acoustic impedance depends on both the characteristics of the wave and the medium. The local instantaneous sound intensity is the product of the sound pressure and the acoustic particle velocity and is, therefore, a vector quantity.

The sound pressure deviation (instantaneous acoustic pressure) p is

$p = \frac{F}{A} \,$

where

F = force,

A = area.

The entire pressure p_total is

$p_\mathrm{total} = p_0 + p \,$

where

p₀ = local ambient pressure,

p = sound pressure deviation.

[edit] Sound pressure level

Sound pressure level (SPL) or sound level L_p is a logarithmic measure of the rms sound pressure of a sound relative to a reference value. It is measured in decibels (dB).

$L_p=10 \log_{10}\left(\frac{p^2_{\mathrm{{rms}}}}{p^2_{\mathrm{ref}}}\right) =20 \log_{10}\left(\frac{p_{\mathrm{rms}}}{p_{\mathrm{ref}}}\right)\mbox{ dB} ,$

where $p ref$ is the reference sound pressure and $p rms$ is the rms sound pressure being measured.^[1]

Sometimes variants are used such as dB (SPL), dBSPL, or dB_SPL. These variants are not permitted by SI.^[2]

The unit dB (SPL) is often abbreviated to just "dB", which gives some the erroneous notion that a dB is an absolute unit by itself.^{[contradiction]}

The commonly used reference sound pressure in air is $p ref$ = 20 µPa (rms), which is usually considered the threshold of human hearing (roughly the sound of a mosquito flying 3 m away). When dealing with hearing, the perceived loudness of a sound correlates roughly logarithmically to its sound pressure. See also Weber-Fechner law. Most measurements of audio equipment will be made relative to this level, meaning 1 pascal will equal 94 dB of sound pressure.

In other media, such as underwater, a reference level of 1 µPa is more often used.^[3]

These references are defined in ANSI S1.1-1994.^[4]

The human ear is a sound pressure sensitive detector. It does not have a flat spectral response, so the sound pressure is often frequency weighted such that the measured level will match the perceived level. When weighted in this way the measurement is referred to as a sound level. The International Electrotechnical Commission (IEC) has defined several weighting schemes. A-weighting attempts to match the response of the human ear to pure tones, while C-weighting is used to measure peak sound levels.^[5] If the (unweighted) SPL is desired, many instruments allow a "flat" or unweighted measurement to be made. See also Weighting filter.

When measuring the sound created by an object, it is important to measure the distance from the object as well, since the SPL decreases in distance from a point source with 1/r (and not with 1/r², like sound intensity). It often varies in direction from the source, as well, so many measurements may be necessary, depending on the situation. An obvious example of a source that varies in level in different directions is a bullhorn.

Sound pressure p in N/m² or Pa is

$p = Zv = \frac{J}{v} = \sqrt{JZ} \,$

where

Z is acoustic impedance, sound impedance, or characteristic impedance, in Pa·s/m

v is particle velocity in m/s

J is acoustic intensity or sound intensity, in W/m²

Sound pressure p is connected to particle displacement (or particle amplitude) ξ, in m, by

$\xi = \frac{v}{2 \pi f} = \frac{v}{\omega} = \frac{p}{Z \omega} = \frac{p}{ 2 \pi f Z} \,$ .

Sound pressure p is

$p = \rho c \omega \xi = Z \omega \xi = { 2 \pi f \xi Z} = \frac{a Z}{\omega} = c \sqrt{\rho E} = \sqrt{\frac{P_{ac} Z}{A}} \,$ ,

normally in units of N/m² = Pa.

where:

Symbol	SI Unit	Meaning
p	pascals	sound pressure
f	hertz	frequency
ρ	kg/m³	density of air
c	m/s	speed of sound
v	m/s	particle velocity
$ω$ = 2 · $π$ · f	radians/s	angular frequency
ξ	meters	particle displacement
Z = c • ρ	N·s/m³	acoustic impedance
a	m/s²	particle acceleration
J	W/m²	sound intensity
E	W·s/m³	sound energy density
P_ac	watts	sound power or acoustic power
A	m²	Area

The distance law for the sound pressure p is inverse-proportional to the distance r of a punctual sound source.

$p \propto \frac{1}{r} \,$ (proportional)

$\frac{p_1} {p_2} = \frac{r_2}{r_1} \,$

$p_1 = p_{2} \cdot r_{2} \cdot \frac{1}{r_1} \,$

The assumption of 1/r² with the square is here wrong. That is only correct for sound intensity.

Note: The often used term "intensity of sound pressure" is not correct. Use "magnitude", "strength", "amplitude", or "level" instead. "Sound intensity" is sound power per unit area, while "pressure" is a measure of force per unit area. Intensity is not equivalent to pressure.

$I \sim {p^2} \sim \dfrac{1}{r^2} \,$

Hence $p \sim \dfrac{1}{r} \,$

[edit] Examples of sound pressure and sound pressure levels

Sound pressure in air:

Source of sound	Sound pressure	Sound pressure level
	pascal	dB re 20 μPa
Krakatoa explosion at 100 miles (160 km) in air^{[dubious – discuss]}	20,000 Pa	180 dB
Simple open-ended thermoacoustic device ^[6]	12,619 Pa	176 dB
.30-06 carbine 1 m to shooter's left side	7,265 Pa	171 dB (peak)
M1 Garand being fired at 1 m	5,023 Pa	168 dB
Jet engine at 30 m	632 Pa	150 dB
Threshold of pain	63.2 Pa	130 dB
Hearing damage (due to short-term exposure)	20 Pa	approx. 115 dB
Jet at 100 m	6.32 – 200 Pa	110 – 140 dB
Jack hammer at 1 m	2 Pa	approx. 100 dB
Hearing damage (due to long-term exposure)	0.356 Pa	78 dB
Major road at 10 m	2×10⁻¹ – 6.32×10⁻¹ Pa	80 – 90 dB
Passenger car at 10 m	2×10⁻² – 2×10⁻¹ Pa	60 – 80 dB
TV (set at home level) at 1 m	2×10⁻² Pa	approx. 60 dB
Normal talking at 1 m	2×10⁻³ – 2×10⁻² Pa	40 – 60 dB
Very calm room	2×10⁻⁴ – 6.32×10⁻⁴ Pa	20 – 30 dB
Leaves rustling, calm breathing	6.32×10⁻⁵ Pa	10 dB
Auditory threshold at 1 kHz	2×10⁻⁵ Pa	0 dB

Sound pressure in water:

Source of sound	Sound pressure	Sound pressure level
	pascal	dB re 1 μPa
Pistol shrimp		218 dB^[7]
Sperm Whale		163-180 dB^[8]
Fin Whale		160-186 dB^[9]
Humpback Whale		144-174 dB^[10]
Bowhead Whale		128-189 dB^[11]
Blue Whale		155-188 dB^[12]
Southern Right Whale		172-187 dB^[13]
Gray Whale		142-185 dB^[14]
Auditory threshold of a diver at 1 kHz	2.2 × 10⁻³ Pa	67 dB^[15]

The formula for the sum of the sound pressure levels of n incoherent radiating sources is

$L_\Sigma = 10\,\cdot\,{\rm log}_{10} \left(\frac{p^2_1 + p^2_2 + \cdots + p^2_n}{p^2_{\mathrm{ref}}}\right) = 10\,\cdot\,{\rm log}_{10} \left(\left({\frac{p_1}{p_{\mathrm{ref}}}}\right)^2 + \left({\frac{p_2}{p_{\mathrm{ref}}}}\right)^2 + \cdots + \left({\frac{p_n}{p_{\mathrm{ref}}}}\right)^2\right)$

From the formula of the sound pressure level we find

$\left({\frac{p_i}{p_{\mathrm{ref}}}}\right)^2 = 10^{\frac{L_i}{10}},\qquad i=1,2,\cdots,n$

This inserted in the formula for the sound pressure level to calculate the sum level shows

$L_\Sigma = 10\,\cdot\,{\rm log}_{10} \left(10^{\frac{L_1}{10}} + 10^{\frac{L_2}{10}} + \cdots + 10^{\frac{L_n}{10}} \right)\,{\rm dB}$

[edit] See also

Acoustics
amplitude
decibel, especially the Acoustics section
phon (unit)
loudness
sone (unit)
sound level meter
sound power level
Stevens' power law
Weber–Fechner law, especially The case of sound

[edit] Notes and References

^ Sometimes reference sound pressure is denoted p₀, not to be confused with the (much higher) ambient pressure.
^ Taylor 1995, Guide for the Use of the International System of Units (SI), NIST Special Publication SP811
^ C. L. Morfey, Dictionary of Acoustics (Academic Press, San Diego, 2001).
^ Glossary of Noise Terms — Sound pressure level definition
^ Glossary of Terms — Cirrus Research plc.
^ Hatazawa, M., Sugita, H., Ogawa, T. & Seo, Y. (Jan. 2004), ‘Performance of a thermoacoustic sound wave generator driven with waste heat of automobile gasoline engine,’ Transactions of the Japan Society of Mechanical Engineers (Part B) Vol. 16, No. 1, 292–299. [1]
^ http://www.dailymail.co.uk/sciencetech/article-1085398/Deadly-pistol-shrimp-stuns-prey-sound-loud-Concorde-UK-waters.html
^ http://www.surtass-lfa-eis.com/Terms/
^ http://www.surtass-lfa-eis.com/Terms/
^ http://www.surtass-lfa-eis.com/Terms/
^ http://www.surtass-lfa-eis.com/Terms/
^ http://www.surtass-lfa-eis.com/Terms/
^ http://www.surtass-lfa-eis.com/Terms/
^ http://www.surtass-lfa-eis.com/Terms/
^ Parvin S.J., Searle S.L. and Gilbert M.J. (2001). "Exposure of divers to underwater sound in the frequency range from to 2250 Hz". Undersea Hyperb Med. Abstract 28 (Supl). ISSN 1066-2936. OCLC 26915585. http://archive.rubicon-foundation.org/984. Retrieved on 2008-05-05.

Beranek, Leo L, "Acoustics" (1993) Acoustical Society of America. ISBN 0-88318-494-X
Morfey, Christopher L, "Dictionary of Acoustics" (2001) Academic Press, San Diego.

[edit] External links

[0] Sometimes reference sound pressure is denoted p₀, not to be confused with the (much higher) ambient pressure.

[1] Taylor 1995, Guide for the Use of the International System of Units (SI), NIST Special Publication SP811

[Morfey-2] C. L. Morfey, Dictionary of Acoustics (Academic Press, San Diego, 2001).

[3] Glossary of Noise Terms — Sound pressure level definition

[4] Glossary of Terms — Cirrus Research plc.

[5] Hatazawa, M., Sugita, H., Ogawa, T. & Seo, Y. (Jan. 2004), ‘Performance of a thermoacoustic sound wave generator driven with waste heat of automobile gasoline engine,’ Transactions of the Japan Society of Mechanical Engineers (Part B) Vol. 16, No. 1, 292–299. [1]

[6] ttp://www.dailymail.co.uk/sciencetech/article-1085398/Deadly-pistol-shrimp-stuns-prey-sound-loud-Concorde-UK-waters.html

[7] ttp://www.surtass-lfa-eis.com/Terms/

[8] ttp://www.surtass-lfa-eis.com/Terms/

[9] ttp://www.surtass-lfa-eis.com/Terms/

[10] ttp://www.surtass-lfa-eis.com/Terms/

[11] ttp://www.surtass-lfa-eis.com/Terms/

[12] ttp://www.surtass-lfa-eis.com/Terms/

[13] ttp://www.surtass-lfa-eis.com/Terms/

[14] Parvin S.J., Searle S.L. and Gilbert M.J. (2001). "Exposure of divers to underwater sound in the frequency range from to 2250 Hz". Undersea Hyperb Med. Abstract 28 (Supl). ISSN 1066-2936. OCLC 26915585. http://archive.rubicon-foundation.org/984. Retrieved on 2008-05-05.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

Sound pressure

From Wikipedia, the free encyclopedia

Contents

[edit] Sound pressure level

[edit] Examples of sound pressure and sound pressure levels

[edit] See also

[edit] Notes and References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages