Musical acoustics

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Musical acoustics or music acoustics is the branch of acoustics concerned with researching and describing the physics of music — how sounds employed as music work. Examples of areas of study are the function of musical instruments, the human voice (the physics of speech and singing), computer analysis of melody.

Contents

[edit] Methods and fields of study

[edit] Physical aspects

Whenever two different pitches are played at the same time, their sound waves interact with each other — the highs and lows in the air pressure reinforce each other to produce a different sound wave. As a result, any given sound wave which is more complicated than a sine wave can be modelled by many different sine waves of the appropriate frequencies and amplitudes (a frequency spectrum). In humans the hearing apparatus (composed of the ears and brain) can usually isolate these tones and hear them distinctly. When two or more tones are played at once, a variation of air pressure at the ear "contains" the pitches of each, and the ear and/or brain isolate and decode them into distinct tones.

When the original sound sources are perfectly periodic, the note consists of several related sine waves (which mathematically add to each other) called the fundamental and the harmonics, partials, or overtones. The sounds have harmonic frequency spectra. The lowest frequency present is the fundamental, and is the frequency at which the entire wave vibrates. The overtones vibrate faster than the fundamental, but must vibrate at integer multiples of the fundamental frequency in order for the total wave to be exactly the same each cycle. Real instruments are close to periodic, but the frequencies of the overtones are slightly imperfect, so the shape of the wave changes slightly over time[citation needed].

[edit] Subjective aspects

Variations in air pressure against the ear drum, and the subsequent physical and neurological processing and interpretation, give rise to the subjective experience called "sound". Most sound that people recognize as "musical" is dominated by periodic or regular vibrations rather than non-periodic ones (called a definite pitch), and we refer to the transmission mechanism as a "sound wave". In a very simple case, the sound of a sine wave, which is considered to be the most basic model of a sound waveform, causes the air pressure to increase and decrease in a regular fashion, and is heard as a very "pure" tone. Pure tones can be produced by tuning forks or whistling. The rate at which the air pressure varies governs is the frequency of the tone, which is measured in oscillations per second, called hertz. Frequency is a primary determinate of the perceived pitch. Frequency can change with Altitude due to changes in air pressure. This is called the Adiabatic Lapse Rate

[edit] Frequency Range of Music

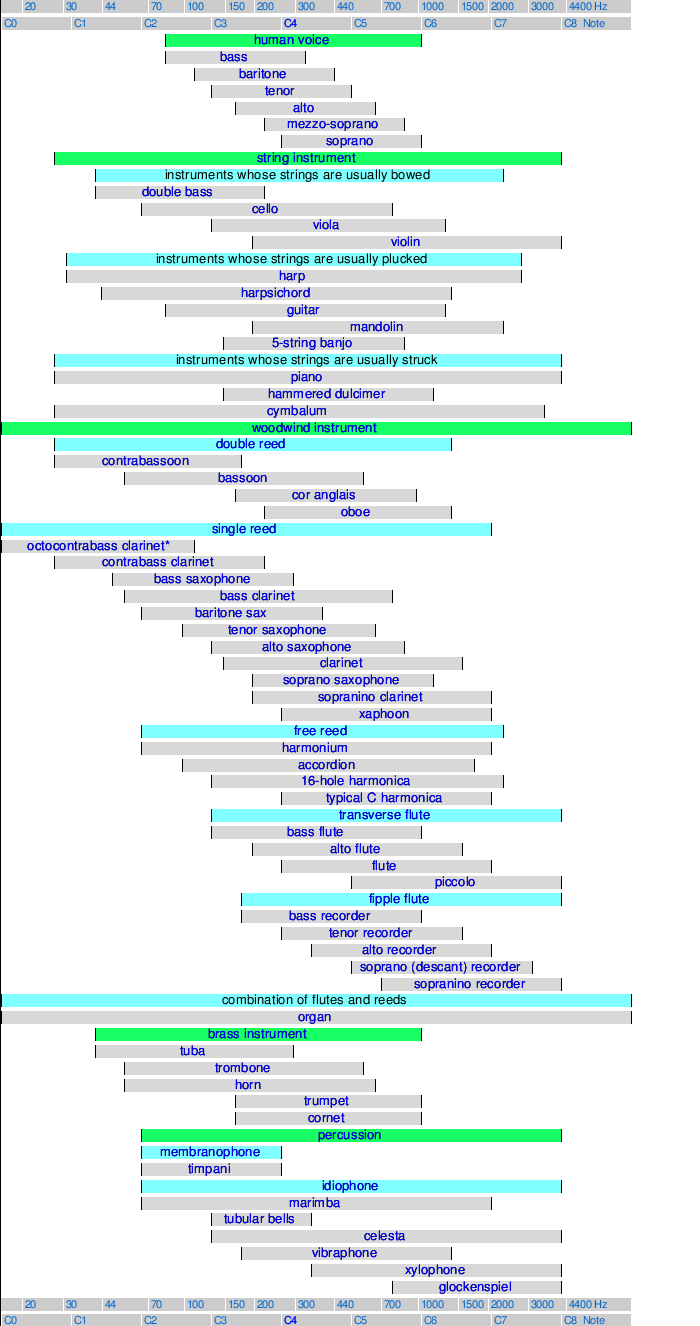
*This chart only displays to a C0, though the octocontrabass clarinet extends down the B♭ below that C.


A spectrogram of violin playing. The bright lines along the bottom are the fundamentals of each note, and the other bright lines are (nearly) harmonic overtones; collectively, they are spectra.

[edit] Harmonics, partials, and overtones

Scale of harmonics

The fundamental is the frequency at which the entire wave vibrates. Overtones are other sinusoidal components present at frequencies above the fundamental. All of the frequency components that make up the total waveform, including the fundamental and the overtones, are called partials. Together they form the harmonic series.

Overtones which are perfect integer multiples of the fundamental are called harmonics. When an overtone is near to being harmonic, but not exact, it is sometimes called a harmonic partial, although they are often referred to simply as harmonics. Sometimes overtones are created that are not anywhere near a harmonic, and are just called partials or inharmonic overtones.

The fundamental frequency is considered the first harmonic and the first partial. The numbering of the partials and harmonics is then usually the same; the second partial is the second harmonic, etc. But if there are inharmonic partials, the numbering no longer coincides. Overtones are numbered as they appear above the fundamental. So strictly speaking, the first overtone is the second partial (and usually the second harmonic). As this can result in confusion, only harmonics are usually referred to by their numbers, and overtones and partials are described by their relationships to those harmonics.

[edit] Harmonics and non-linearities

A half-wave symmetric and asymmetric waveform. The red contains only the fundamental and odd harmonics, the green contains the fundamental, odd, and even harmonics.
200 and 300 Hz waves and their sum, showing the periods of each.
A spectrogram of a violin playing a note and then a perfect fifth above it. The shared partials are highlighted by the white dashes.

When a periodic wave is composed of a fundamental and only odd harmonics (f, 3f, 5f, 7f, ...), the summed wave is half-wave symmetric; it can be inverted and phase shifted and be exactly the same. If the wave has any even harmonics (0f, 2f, 4f, 6f, ...), it will be asymmetrical; the top half will not be a mirror image of the bottom.

The opposite is also true. A system which changes the shape of the wave (beyond simple scaling or shifting) creates additional harmonics (harmonic distortion). This is called a non-linear system. If it affects the wave symmetrically, the harmonics produced will only be odd, if asymmetrically, at least one even harmonic will be produced (and probably also odd).

[edit] Harmony

Main article: Harmony

If two notes are simultaneously played, with frequency ratios that are simple fractions (e.g. 2/1, 3/2 or 5/4), then the composite wave will still be periodic with a short period, and the combination will sound consonant. For instance, a note vibrating at 200 Hz and a note vibrating at 300 Hz (a perfect fifth, or 3/2 ratio, above 200 Hz) will add together to make a wave that repeats at 100 Hz: every 1/100 of a second, the 300 Hz wave will repeat thrice and the 200 Hz wave will repeat twice. Note that the total wave repeats at 100 Hz, but there is not actually a 100 Hz sinusoidal component present.

Additionally, the two notes will have many of the same partials. For instance, a note with a fundamental frequency of 200 Hz will have harmonics at:

(200,) 400, 600, 800, 1000, 1200, …

A note with fundamental frequency of 300 Hz will have harmonics at:

(300,) 600, 900, 1200, 1500, …

The two notes have the harmonics 600 and 1200 in common, and more will coincide further up the series.

The combination of composite waves with short fundamental frequencies and shared or closely related partials is what causes the sensation of harmony.

When two frequencies are near to a simple fraction, but not exact, the composite wave cycles slowly enough to hear the cancellation of the waves as a steady pulsing instead of a tone. This is called beating, and is considered to be unpleasant, or dissonant.

The frequency of beating is calculated as the difference between the frequencies of the two notes. For the example above, |200 Hz - 300 Hz| = 100 Hz. As another example, a combination of 3425 Hz and 3426 Hz would beat once per second (|3425 Hz - 3426 Hz| = 1 Hz). This follows from modulation theory.

The difference between consonance and dissonance is not clearly defined, but the higher the beat frequency, the more likely the interval to be dissonant. Helmholtz proposed that maximum dissonance would arise between two pure tones when the beat rate is roughly 35 Hz. [1]

[edit] Scales

Main article: Musical scale

The material of a musical composition is usually taken from a collection of pitches known as a scale. Because most people cannot adequately determine absolute frequencies, the identity of a scale lies in the ratios of frequencies between its tones (known as intervals).

Main article: Just intonation

The diatonic scale appears in writing throughout history, consisting of seven tones in each octave. In just intonation the diatonic scale may be easily constructed using the three simplest intervals within the octave, the perfect fifth (3/2), perfect fourth (4/3), and the major third (5/4). As forms of the fifth and third are naturally present in the overtone series of harmonic resonators, this is a very simple process.

The following table shows the ratios between the frequencies of all the notes of the just major scale and the fixed frequency of the first note of the scale.

C D E F G A B C
1 9/8 5/4 4/3 3/2 5/3 15/8 2

There are other scales available through just intonation, for example the minor scale. Scales which do not adhere to just intonation, and instead have their intervals adjusted to meet other needs are known as temperaments, of which equal temperament is the most used. Temperaments, though they obscure the acoustical purity of just intervals often have other desirable properties, such as a closed circle of fifths.

[edit] Further reading

[edit] See also

Music portal

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Musical_acoustics"
Personal tools