3d 3dgrafika 3dmeasurementmath _games algebra complex geeky graphics groups grouptheory hamilton math mathematics matrix number number_theory physics quaternion quaternions rotationalgeometry science secondlife thesis tolearn vector

My tags:

From Wikipedia, the free encyclopedia

Quaternions, in mathematics, are a non-commutative number system that extends the complex numbers. The quaternions were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. They find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations (see "quaternions and spatial rotation"), such as in 3D computer graphics, although they have been superseded in many applications by vectors and matrices.

In modern language, quaternions form a 4-dimensional normed division algebra over the real numbers. The algebra of quaternions is often denoted by H (for Hamilton), or in blackboard bold by 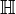(Unicode ℍ). It can also be given by the Clifford algebra classifications Cℓ_0,2(R) = Cℓ⁰_3,0(R). The algebra H holds a special place in analysis since, according to the Frobenius theorem, it is one of only two finite-dimensional division rings containing the real numbers as a proper subring, the other being the complex numbers.

Contents 1 History 2 Definition 2.1 Multiplication of basis elements 2.2 Hamilton product 2.3 Ordered list form 2.4 Remarks 2.4.1 Scalar and vector parts 2.4.2 Non-commutativity 2.4.3 Historical impact on physics 3 Conjugation, the norm, and division 4 Algebraic properties 5 Quaternions and the geometry of R3 6 Matrix representations 7 Quaternions as pairs of complex numbers 8 Square roots of −1 8.1 H as a union of complex planes 8.2 Commutative subrings 9 Functions of a quaternion variable 10 Three-dimensional and four-dimensional rotation groups 11 Generalizations 12 Quaternions as the even part of Cℓ3,0(R) 13 Quotes 14 See also 15 Notes 16 External articles and resources 16.1 Books and publications 16.2 Links and monographs 16.3 Software

[edit] History

Quaternions were introduced by Irish mathematician Sir William Rowan Hamilton in 1843. Hamilton knew that the complex numbers could be viewed as points in a plane, and he was looking for a way to do the same for points in space. Points in space can be represented by their coordinates, which are triples of numbers, and for many years Hamilton had known how to add and multiply triples of numbers. But he had been stuck on the problem of division: He did not know how to take the quotient of two points in space.

On October 16, 1843, Hamilton and his wife took a walk along the Royal Canal in Dublin. While they walked across Brougham Bridge (now Broom Bridge), a solution suddenly occurred to him. He could not divide triples, but he could divide quadruples. By using three of the numbers in the quadruple as the points of a coordinate in space, Hamilton could represent points in space by his new system of numbers. He then carved the basic rules for multiplication into the bridge:

i² = j² = k² = ijk = − 1.

Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted the remainder of his life to studying and teaching them. He founded a school of "quaternionists" and popularized them in several books. The last and longest, Elements of Quaternions, had 800 pages and was published shortly after his death.

After Hamilton's death, his pupil Peter Tait continued promoting quaternions. At this time, quaternions were a mandatory examination topic in Dublin, and in some American universities they were the only advanced mathematics topic taught. Topics in physics and geometry that would now be described using vectors, such as kinematics in space and Maxwell's equations, were described entirely in terms of quaternions. There was even a professional research association, the Quaternion Society, exclusively devoted to the study of quaternions.

From the mid 1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs and Oliver Heaviside. Vector analysis described the same phenomena as quaternions, so it borrowed ideas and terms liberally from the classical quaternion literature. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics and physics. A side effect of this transition is that Hamilton's work is difficult to comprehend for many modern readers because they think only in the familiar terms they learned from vector analysis, and Hamilton's original definitions are both unfamiliar to them and fundamentally different.

However, quaternions have had a revival in the late 20th century, primarily due to their utility in describing spatial rotations. Representations of rotations by quaternions are more compact and faster to compute than representations by matrices. For this reason, quaternions are used in computer graphics,^[1] control theory, signal processing, attitude control, physics, bioinformatics, and orbital mechanics. For example, it is common for spacecraft attitude-control systems to be commanded in terms of quaternions. Quaternions have received another boost from number theory because of their relation to quadratic forms.

Since 1989, the Department of Mathematics of the National University of Ireland, Maynooth has organized a pilgrimage, where scientists (including physicists Murray Gell-Mann in 2002, Steven Weinberg in 2005, and mathematician Andrew Wiles in 2003) take a walk from Dunsink Observatory to the Royal Canal bridge where, unfortunately, no trace of Hamilton's carving remains.

[edit] Definition

As a set, the quaternions H are equal to R⁴, a four-dimensional vector space over the real numbers. H has three operations: Addition, scalar multiplication, and quaternion multiplication. The sum of two elements of H is defined to be their sum as elements of R⁴. Similarly the product of an element of H by a real number is defined to be the same as the product in R⁴. To define multiplication in H requires a choice of basis for R⁴. The elements of this basis are customarily denoted as 1, i, j, and k. Every element of H can be uniquely written as a linear combination of these basis elements, that is, as a1 + bi + cj + dk, where a, b, c, and d are real numbers. The basis element 1 will be the identity element of H, meaning that multiplication by 1 does nothing, and for this reason, elements of H are usually written a + bi + cj + dk, suppressing the basis element 1. Given this basis, quaternion multiplication is defined by first defining the products of basis elements and then defining all other products using the distributive law.

[edit] Multiplication of basis elements

The equations

i² = j² = k² = ijk = − 1,

where i, j, and k are imaginary numbers, determine all the possible products of i, j, and k. For example, since

− 1 = ijk,

right-multiplying both sides by k gives

All the other possible products can be determined by similar methods, and this gives the following table:

[edit] Hamilton product

For two elements a₁ + b₁i + c₁j + d₁k and a₂ + b₂i + c₂j + d₂k, their Hamilton product (a₁ + b₁i + c₁j + d₁k)(a₂ + b₂i + c₂j + d₂k) is determined by the products of the basis elements and the distributive law. The distributive law makes it possible to expand the product so that it is a sum of products of basis elements. This gives the following expression:

a₁a₂ + a₁b₂i + a₁c₂j + a₁d₂k + b₁a₂i + b₁b₂i² + b₁c₂ij + b₁d₂ik + c₁a₂j + c₁b₂ji + c₁c₂j² + c₁d₂jk + d₁a₂k + d₁b₂ki + d₁c₂kj + d₁d₂k².

Now the basis elements can be multiplied using the rules given above to get:

(a₁a₂ − b₁b₂ − c₁c₂ − d₁d₂) + (a₁b₂ + b₁a₂ + c₁d₂ − d₁c₂)i + (a₁c₂ − b₁d₂ + c₁a₂ + d₁b₂)j + (a₁d₂ + b₁c₂ − c₁b₂ + d₁a₂)k.

[edit] Ordered list form

Using the basis 1, i, j, k of H makes it possible to write H as a set of quadruples:

Then the basis elements are:

1 = (1,0,0,0),

i = (0,1,0,0),

j = (0,0,1,0),

k = (0,0,0,1),

and the formulas for addition and multiplication are:

(a₁,b₁,c₁,d₁) + (a₂,b₂,c₂,d₂) = (a₁ + a₂,b₁ + b₂,c₁ + c₂,d₁ + d₂).

(a₁,b₁,c₁,d₁)(a₂,b₂,c₂,d₂) = (a₁a₂ − b₁b₂ − c₁c₂ − d₁d₂,a₁b₂ + b₁a₂ + c₁d₂ − d₁c₂,a₁c₂ − b₁d₂ + c₁a₂ + d₁b₂,a₁d₂ + b₁c₂ − c₁b₂ + d₁a₂).

[edit] Remarks

[edit] Scalar and vector parts

A number of the form a + 0i + 0j + 0k, where a is a real number, is called real, and a number of the form 0 + bi + cj + dk, where b, c, and d are real numbers, is called pure imaginary. If a + bi + cj + dk is any quaternion, then a is called its scalar part and bi + cj + dk is called its vector part. The scalar part of a quaternion is always real, and the vector part is always pure imaginary. Even though every quaternion is a vector in a four-dimensional vector space, it is common to define a vector to mean a pure imaginary quaternion. With this convention, a vector is the same as an element of the vector space R³. This identification leads to many applications.

Hamilton called pure imaginary quaternions right quaternions^[2][3] and real numbers (considered as quaternions with zero vector part) scalar quaternions.

[edit] Non-commutativity

Unlike multiplication of real or complex numbers, multiplication of quaternions is not commutative: For example, ij = k, while ji = − k. The non-commutativity of multiplication has some unexpected consequences, among them that polynomial equations over the quaternions can have more distinct solutions than the degree of the polynomial. The equation z² + 1 = 0, for instance, has infinitely many quaternion solutions z = bi + cj + dk with b² + c² + d² = 1, so that these solutions form a two-dimensional sphere centered on zero in the three-dimensional pure imaginary subspace of quaternions. This sphere intersects the complex plane at the two poles i and  − i.

[edit] Historical impact on physics

Since the real part of the product of two quaternions Q₁: = (a₁,b₁,c₁,d₁) and Q₂: = (a₂,b₂,c₂,d₂) is identical to the Lorentz-invariant part of two four vectors in physics,

Q₁Q₂ | _real = (a₁a₂ − b₁b₂ − c₁c₂ − d₁d₂),

therefore hinting at usability for modeling Minkowski space from Einstein's Special Relativity theory, this has attracted much interest around the 1900s^{[citation needed]}, including formation of a "Quaternion Society". During the 20th century, quaternion algebra has become an integral part of fundamental formulations in quantum mechanics, e.g., in Pauli matrices for modeling Fermion spin, Dirac matrices describing the free equation of motion of a Fermion in Quantum electrodynamics, and for modeling the Weak interaction which governs nuclear decay. In all these formulations, quaternions are typically not used directly, but are embedded into wider matrix formulations over the complex numbers.

[edit] Conjugation, the norm, and division

Conjugation of quaternions is analogous to conjugation of complex numbers and to transposition (also known as reversal) of elements of Clifford algebras. To define it, let q = a +bi +cj + dk be a quaternion. The conjugate of q is the quaternion a − bi − cj − dk. It is denoted by q^*, , q^t, or . Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)^* = q^*p^*, not p^*q^*.

Conjugation can be used to extract the scalar and vector parts of a quaternion. The scalar part of p is (p + p^*)/2, and the vector part of p is (p − p^*)/2.

The square root of the product of a quaternion with its conjugate is called its norm and is denoted ||q||. (Hamilton called this quantity the tensor of q, but this conflicts with modern usage. See tensor.) It has the formula

This is always a non-negative real number, and it is same as the Euclidean norm on H considered as the vector space R⁴. Multiplying a quaternion by a real number scales its norm by the absolute value of the number. That is, if α is real, then

This is a special case of the fact that the norm is multiplicative, meaning that

for any two quaternions p and q. Multiplicativity is a consequence of the formula for the conjugate of a product. This norm makes it possible to define the distance d(p, q) between p and q as the norm of their difference:

This makes H into a metric space. Addition and multiplication are continuous in the metric topology.

A unit quaternion is a quaternion of norm one. Dividing a non-zero quaternion q by its norm produces a unit quaternion Uq called the versor of q:

Using conjugation and the norm makes it possible to define the reciprocal of a quaternion. The product of a quaternion with its reciprocal should equal 1, and the considerations above imply that the product of q and (in either order) is 1. So the reciprocal of q is defined to be

This makes it possible to divide two quaternions p and q in two different ways. That is, their quotient can be either pq⁻¹ or q⁻¹p. The notation p/q is ambiguous because it does not specify whether q divides on the left or the right.

[edit] Algebraic properties

The set H of all quaternions is a vector space over the real numbers with dimension 4. (In comparison, the real numbers have dimension 1, the complex numbers have dimension 2, and the octonions have dimension 8.) They are an associative algebra over the real numbers. Even though they contain copies of the complex numbers, they are not an associative algebra over the complex numbers because multiplying a quaternion by a complex number is not always commutative.

The norm makes the quaternions into a normed algebra, and even into a composition algebra and a unital Banach algebra. Composition algebras are very rare. Hurwitz's theorem states that there are only four composition algebras over the real numbers: R, C, H, and O. Because it is possible to divide quaternions, they form a division algebra. This is a structure similar to a field except for the commutativity of multiplication. Finite-dimensional division algebras over the real numbers are also very rare. The Frobenius theorem states that there are exactly three: R, C, and H.

Because the product of any two basis vectors is plus or minus another basis vector, the set {±1, ±i, ±j, ±k} forms a group under multiplication. This group is called the quaternion group and is denoted Q₈. The real group ring of Q₈ is a ring RQ₈ which is also an eight-dimensional vector space over R. It has one basis vector for each element of Q₈. The quaternions are the quotient ring of RQ₈ by the ideal generated by the elements 1 + (−1), i + (−i), j + (−j), and k + (−k). Here the first term in each of the differences is one of the basis elements 1, i, j, and k, and the second term is one of basis elements −1, −i, −j, and −k, not the additive inverses of 1, i, j, and k.

[edit] Quaternions and the geometry of R³

Because the vector part of a quaternion is a vector in R³, the geometry of R³ is reflected in the algebraic structure of the quaternions. Many operations on vectors can be defined in terms of quaternions, and this makes it possible to apply quaternion techniques wherever spatial vectors arise. For instance, this is true in electrodynamics and 3D computer graphics.

For the remainder of this section, i, j, and k will denote both imaginary^[4] basis vectors of H and a basis for R³. Notice that replacing i by −i, j by −j, and k by −k sends a vector to its additive inverse, so the additive inverse of a vector is the same as its conjugate as a quaternion. For this reason, conjugation is sometimes called the spatial inverse.

Choose two imaginary quaternions p = b₁i + c₁j + d₁k and q = b₂i + c₂j + d₂k. Their dot product is

This is equal to the scalar parts of p^*q, qp^*, pq^*, and q^*p. (Note that the vector parts of these four products are different.) It also has the formulas

The cross product of p and q relative to the orientation determined by the ordered basis i, j, and k is

(Recall that the orientation is necessary to determine the sign.) This is equal to the vector part of the product pq (as quaternions), as well as the vector part of −q^*p^*. It also has the formula

In general, let p and q be quaternions (possibly non-imaginary), and write

where p_s and q_s are the scalar parts of p and q 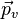and and are the vector parts of p and q. Then we have the formula

This shows that the non-commutativity of quaternion multiplication comes from the multiplication of pure imaginary quaternions. It also shows that two quaternions commute if and only if their vector parts are collinear.

[edit] Matrix representations

There are at least two ways of representing quaternions as matrices in such a way that quaternion addition and multiplication correspond to matrix addition and matrix multiplication. One is to use 2×2 complex matrices, and the other is to use 4×4 real matrices. In the terminology of abstract algebra, these are injective homomorphisms from H to the matrix rings M₂(C) and M₄(R), respectively.

Using 2×2 complex matrices, the quaternion a + bi + cj + dk can be represented as

This representation has the following properties:

• Complex numbers (c = d = 0) correspond to diagonal matrices.
• The norm of a quaternion (the square root of a product with its conjugate, as with complex numbers) is the square root of the determinant of the corresponding matrix.
• The conjugate of a quaternion corresponds to the conjugate transpose of the matrix.
• Restricted to unit quaternions, this representation provides an isomorphism between S³ and SU(2). The latter group is important for describing spin in quantum mechanics; see Pauli matrices.

Using 4×4 real matrices, that same quaternion can be written as

In this representation, the conjugate of a quaternion corresponds to the transpose of the matrix. The fourth power of the norm of a quaternion is the determinant of the corresponding matrix. Complex numbers are block diagonal matrices with two 2×2 blocks.

[edit] Quaternions as pairs of complex numbers

Quaternions can be represented as pairs of complex numbers. From this perspective, quaternions are the result of applying the Cayley–Dickson construction to the complex numbers. This is a generalization of the construction of the complex numbers as pairs of real numbers.

Let C² be a two-dimensional vector space over the complex numbers. Choose a basis consisting of two elements 1 and j. A vector in C² can be written in terms of the basis elements 1 and j as

(a + bi)1 + (c + di)j.

If we define j² = −1 and ij = −ji, then we can multiply two vectors using the distributive law. Writing k in place of the product ij leads to the same rules for multiplication as the usual quaternions. Therefore the above vector of complex numbers corresponds to the quaternion a + bi + cj + dk. If we write the elements of C² as ordered pairs and quaternions as quadruples, then the correspondence is

[edit] Square roots of −1

In the complex numbers, there are just two numbers, i and −i, whose square is −1 . In H there are infinitely many square roots of minus one: the quaternion solution for the square root of −1 includes every point on the surface of the unit sphere in 3-space. To see this, let q = a + bi + cj + dk be a quaternion, and assume that its square is −1. In terms of a, b, c, and d, this means

a² − b² − c² − d² = − 1,

2ab = 0,

2ac = 0,

2ad = 0.

To satisfy the last three equations, either a = 0 or b, c, and d are all 0. The latter is impossible because a is a real number and the first equation would imply that a² = −1. Therefore a = 0 and b² + c² + d² = 1. In other words, a quaternion squares to −1 if and only if it is a vector (that is, pure imaginary) with norm 1. By definition, the set of all such vectors forms the unit sphere.

This identification of the square roots of minus one in H is sometimes neglected in expositions of this algebra, especially in early work. By 1971 the fact was included by Sam Perlis in his three page exposition included in Historical Topics in Algebra (page 39) published by the National Council of Teachers of Mathematics. More recently, the sphere of square roots of minus one is described in Ian R. Porteus's book Clifford Algebras and the Classical Groups (Cambridge, 1995) in proposition 8.13 on page 60. Also in Conway (2003) On Quaternions and Octonions we read on page 40: "any imaginary unit may be called i, and perpendicular one j, and their product k", another statement of the sphere.

[edit] H as a union of complex planes

Each square root of −1 creates a distinct copy of the complex numbers inside the quaternions. If q² = −1, then the copy is determined by the function

In the language of abstract algebra, this is an injective ring homomorphism from C to H.

Every non-real quaternion lies in a unique copy of C. Write q as the sum of its scalar part and its vector part:

Decompose the vector part further as the product of its norm and its versor:

(Note that this is not the same as 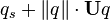.) The versor of the vector part of q, 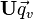, is a pure imaginary unit quaternion, so its square is −1. Therefore it determines a copy of the complex numbers by the function

Under this function, q is the image of the complex number . Thus H is the union of complex planes intersecting in a common real line, where the union is taken over the sphere of square roots of minus one.

[edit] Commutative subrings

The relationship of quaternions to each other within the complex subplanes of H can also be identified and expressed in terms of commutative subrings. Specifically, since two quaternions p and q commute (p q = q p) only if they lie in the same complex subplane of H, the profile of H as a union of complex planes arises when one seeks to find all commutative subrings of the quaternion ring. This method of commutative subrings is also used to profile the coquaternions and real matrices (2 x 2).

[edit] Functions of a quaternion variable

Many functions of a complex variable can be extended to functions of a quaternion variable. Suppose that f is a holomorphic function. Write f as the sum of its real and imaginary parts, that is, as f(x + iy) = u(x,y) + iv(x,y), where u and v are real-valued functions of two real variables. According to the above desciprtion, any quaternion q can be written as q = a + br, where r² = −1. Then f can be extended to quaternions by setting f(q) = u(a,b) + rv(a,b).

There is one restriction on the allowable functions f. Because q is also equal to q = a − br ^* , this function is well-defined only when f commutes with complex conjugation. Equivalently, it is only defined when u is an even function of y and v is an odd function of y.

The great success of complex analysis in providing a rich family of holomorphic functions for scientific work has engaged some workers in efforts to extend the planar theory, based on complex numbers, to a 4-space study with functions of a quaternion variable. These efforts were summarized in 1973 by C.A. Deavours in his article “The Quaternion Calculus” for the American Mathematical Monthly (80:995-1008). Since Hamilton it has been realized that the independence of the derivative from the path that a differential follows toward zero is an onerous restriction, excluding even q². In a 1935 issue of Commentarii Mathematici Helvetici, an alternative theory of “regular functions” was initiated by R. Feuter through the idea of Morera's theorem: quaternion function F is “left regular at q ” when the integral of F vanishes over any sufficiently small hypersurface containing q. Then the analogue of Liouville's theorem holds: the only quaternion function regular with bounded norm in E⁴ is a constant. To construct regular functions, Feuter and Deavours use the profile method, given above, and power series with real coefficients. Analogues are also given for the Poisson integral, the Cauchy integral formula, and the presentation of Maxwell’s equations of electromagnetism with quaternion functions.

[edit] Three-dimensional and four-dimensional rotation groups

The multiplicative group of non-zero quaternions acts by conjugation on the copy of R³ consisting of quaternions with real part equal to zero. The conjugation by a unit quaternion (a quaternion of absolute value 1) with real part cos(t) is a rotation by an angle 2t, the axis of the rotation being the direction of the imaginary part. The advantages of quaternions are:

1. Non singular representation (compared with Euler angles for example)
2. More compact (and faster) than matrices
3. Pairs of unit quaternions represent a rotation in 4D space (see SO(4): Algebra of 4D rotations).

The set of all unit quaternions (versors) forms a 3-dimensional sphere S³ and a group (a Lie group) under multiplication. S³ is the double cover of the group SO(3,R) of real orthogonal 3×3 matrices of determinant 1 since two unit quaternions correspond to every rotation under the above correspondence.

The image of a subgroup of S³ is a point group, and conversely, the preimage of a point group is a subgroup of S³. The preimage of a finite point group is called by the same name, with the prefix binary. For instance, the preimage of the icosahedral group is the binary icosahedral group.

The group S³ is isomorphic to SU(2), the group of complex unitary 2×2 matrices of determinant 1. Let A be the set of quaternions of the form a + bi + cj + dk where a, b, c, and d are either all integers or all rational numbers with odd numerator and denominator 2. The set A is a ring and a lattice. There are 24 unit quaternions in this ring, and they are the vertices of a 24-cell regular polytope with Schläfli symbol {3,4,3}.

[edit] Generalizations

If F is any field with characteristic different from 2, and a and b are elements of F, one may define a four-dimensional unitary associative algebra over F with basis 1, i, j, and ij, where i² = a, j² = b and ij = −ji (so ij² = −ab). These algebras are called quaternion algebras and are isomorphic to the algebra of 2×2 matrices over F or form division algebras over F, depending on the choice of a and b.

[edit] Quaternions as the even part of Cℓ_3,0(R)

The usefulness of quaternions for geometrical computations can be generalised to other dimensions, by identifying the quaternions as the even part Cℓ⁺_3,0(R) of the Clifford algebra Cℓ_3,0(R). This is an associative multivector algebra built up from fundamental basis elements σ₁, σ₂, σ₃ using the product rules

If these fundamental basis elements are taken to represent vectors in 3D space, then it turns out that the reflection of a vector r in a plane perpendicular to a unit vector w can be written:

Now in geometry, two reflections make a rotation, by an angle twice the angle between the two reflection planes, so

corresponds to a rotation of 180° in the plane containing σ₁ and σ₂

But this is very similar to the corresponding quaternion formula,

In fact, the two are identical, if we make the identification

and it is straightforward to confirm that this preserves the Hamilton relations

In this picture, quaternions correspond not to vectors but to bivectors, quantities with magnitude and orientations associated with particular 2D planes rather than 1D directions. The relation to complex numbers becomes clearer, too: in 2D, with two vector directions σ₁ and σ₂, there is only one bivector basis element σ₁σ₂, so only one imaginary. But in 3D, with three vector directions, there are three bivector basis elements σ₁σ₂, σ₂σ₃, σ₃σ₁, so three imaginaries.

With this recognition, the sequence can be continued. So in the Clifford algebra Cℓ_4,0(R), there are six bivector basis elements, since with four different basic vector directions, six different pairs and therefore six different linearly independent planes can be defined. Rotations in such spaces using these generalisations of quaternions, called rotors, can be very useful for applications involving homogeneous coordinates. But it is only in 3D that the number of basis bivectors equals the number of basis vectors, and each bivector can be identified as a pseudovector.

Dorst et al identify the following advantages for placing quaternions in this wider setting:^[5]

• Rotors are natural and non-mysterious in geometric algebra and easily understood as the encoding of a double reflection.
• In geometric algebra, a rotor and the objects it acts on live in the same space. This eliminates the need to change representations and to encode new data structures and methods (which is required when augmenting linear algebra with quaternions).
• A rotor is universally applicable to any element of the algebra, not just vectors and other quaternions, but also lines, planes, circles, spheres, rays, and so on.
• In the conformal model of Euclidean geometry, rotors allow the encoding of rotation, translation and scaling in a single element of the algebra, universally acting on any element. In particular, this means that rotors can represent rotations around an arbitary axis, whereas quaternions are limited to an axis through the origin.
• Rotor-encoded transformations make interpolation particularly straightforward.

For further detail about the geometrical uses of Clifford algebras, see Geometric algebra.

[edit] Quotes

• "I regard it as an inelegance, or imperfection, in quaternions, or rather in the state to which it has been hitherto unfolded, whenever it becomes or seems to become necessary to have recourse to x, y, z, etc." — William Rowan Hamilton (ed. Quoted in a letter from Tait to Cayley.)
• "Time is said to have only one dimension, and space to have three dimensions. […] The mathematical quaternion partakes of both these elements; in technical language it may be said to be "time plus space", or "space plus time": and in this sense it has, or at least involves a reference to, four dimensions. And how the One of Time, of Space the Three, Might in the Chain of Symbols girdled be." — William Rowan Hamilton (Quoted in R.P. Graves, "Life of Sir William Rowan Hamilton")
• "Quaternions came from Hamilton after his really good work had been done; and, though beautifully ingenious, have been an unmixed evil to those who have touched them in any way, including Clerk Maxwell." — Lord Kelvin, 1892.
• "Neither matrices nor quaternions and ordinary vectors were banished from these ten [additional] chapters. For, in spite of the uncontested power of the modern Tensor Calculus, those older mathematical languages continue, in my opinion, to offer conspicuous advantages in the restricted field of special relativity. Moreover, in science as well as in every-day life, the mastery of more than one language is also precious, as it broadens our views, is conducive to criticism with regard to, and guards against hypostasy [weak-foundation] of, the matter expressed by words or mathematical symbols." — Ludwik Silberstein, preparing the second edition of his Theory of Relativity in 1924
• "… quaternions appear to exude an air of nineteenth century decay, as a rather unsuccessful species in the struggle-for-life of mathematical ideas. Mathematicians, admittedly, still keep a warm place in their hearts for the remarkable algebraic properties of quaternions but, alas, such enthusiasm means little to the harder-headed physical scientist." — Simon L. Altmann, 1986
• "...the thing about a Quaternion 'is' is that we're obliged to encounter it in more than one guise. As a vector quotient. As a way of plotting complex numbers along three axes instead of two. As a list of instructions for turning one vector into another..... And considered subjectively, as an act of becoming longer or shorter, while at the same time turning, among axes whose unit vector is not the familiar and comforting 'one' but the altogether disquieting square root of minus one. If you were a vector, mademoiselle, you would begin in the 'real' world, change your length, enter an 'imaginary' reference system, rotate up to three different ways, and return to 'reality' a new person. Or vector..." Thomas Pynchon

[edit] See also

[edit] Notes

[edit] External articles and resources

Look up quaternion in Wiktionary, the free dictionary.

[edit] Books and publications

• Hamilton, William Rowan (1853), "Lectures on Quaternions". Royal Irish Academy.
• Tait, Peter Guthrie (1873), "An elementary treatise on quaternions". 2d ed., Cambridge, [Eng.] : The University Press.
• Maxwell, James Clerk (1873), "A Treatise on Electricity and Magnetism". Clarendon Press, Oxford.
• Tait, Peter Guthrie (1886), "Quaternion". M.A. Sec. R.S.E. Encyclopaedia Britannica, Ninth Edition, 1886, Vol. XX, pp. 160–164. (bzipped PostScript file)
• Joly, Charles Jasper (1905), "A manual of quaternions". London, Macmillan and co., limited; New York, The Macmillan company. LCCN 05036137 //r84
• Macfarlane, Alexander (1906), "Vector analysis and quaternions", 4th ed. 1st thousand. New York, J. Wiley & Sons; [etc., etc.]. LCCN es 16000048
• 1911 encyclopedia: "Quaternions".
• Finkelstein, David, Josef M. Jauch, Samuel Schiminovich, and David Speiser (1962), "Foundations of quaternion quantum mechanics". J. Mathematical Phys. 3, pp. 207–220, MathSciNet.
• Du Val, Patrick (1964), "Homographies, quaternions, and rotations". Oxford, Clarendon Press (Oxford mathematical monographs). LCCN 64056979 //r81
• Crowe, Michael J. (1967), "A History of Vector Analysis: The Evolution of the Idea of a Vectorial System". University of Notre Dame Press. Surveys the major and minor vector systems of the 19th century (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, MacFarlane, MacAuley, Gibbs, Heaviside). The competition between quaternions and other systems is a major theme.
• Altmann, Simon L. (1986), "Rotations, quaternions, and double groups". Oxford [Oxfordshire] : Clarendon Press ; New York : Oxford University Press. LCCN 85013615 ISBN 0-19-855372-2
• Adler, Stephen L. (1995), "Quaternionic quantum mechanics and quantum fields". New York : Oxford University Press. International series of monographs on physics (Oxford, England) 88. LCCN 94006306 ISBN 0-19-506643-X
• Trifonov, Vladimir (1995), "A Linear Solution of the Four-Dimensionality Problem", Europhysics Letters, 32 (8) 621–626, DOI: 10.1209/0295-5075/32/8/001
• Ward, J. P. (1997), "Quaternions and Cayley Numbers: Algebra and Applications", Kluwer Academic Publishers. ISBN 0-7923-4513-4
• Kantor, I. L. and Solodnikov, A. S. (1989), "Hypercomplex numbers, an elementary introduction to algebras", Springer-Verlag, New York, ISBN 0-387-96980-2
• Gürlebeck, Klaus and Sprössig, Wolfgang (1997), "Quaternionic and Clifford calculus for physicists and engineers". Chichester ; New York : Wiley (Mathematical methods in practice; v. 1). LCCN 98169958 ISBN 0-471-96200-7
• Kuipers, Jack (2002), "Quaternions and Rotation Sequences: A Primer With Applications to Orbits, Aerospace, and Virtual Reality" (reprint edition), Princeton University Press. ISBN 0-691-10298-8
• Conway, John Horton, and Smith, Derek A. (2003), "On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry", A. K. Peters, Ltd. ISBN 1-56881-134-9 (review).
• Kravchenko, Vladislav (2003), "Applied Quaternionic Analysis", Heldermann Verlag ISBN 3-88538-228-8.
• Hanson, Andrew J. (2006), "Visualizing Quaternions", Elsevier: Morgan Kaufmann; San Francisco. ISBN 0-12-088400-3
• Trifonov, Vladimir (2007), "Natural Geometry of Nonzero Quaternions", International Journal of Theoretical Physics, 46 (2) 251–257, DOI: 10.1007/s10773-006-9234-9

[edit] Links and monographs

• Matrix and Quaternion FAQ v1.21 Frequently Asked Questions
• Geometric Tools documentation Includes several papers focusing on computer graphics applications of quaternions. Covers useful techniques such as spherical linear interpolation.
• Patrick-Gilles Maillot Provides free Fortran and C source code for manipulating quaternions and rotations / position in space. Also includes mathematical background on quaternions.
• Geometric Tools source code Includes free C++ source code for a complete quaternion class suitable for computer graphics work, under a very liberal license.
• Doug Sweetser, Doing Physics with Quaternions
• Quaternions for Computer Graphics and Mechanics (Gernot Hoffman)
• The Physical Heritage of Sir W. R. Hamilton (PDF)
• D. R. Wilkins, Hamilton’s Research on Quaternions
• Quaternion Julia Fractals 3D Raytraced Quaternion Julia Fractals by David J. Grossman
• Quaternion Math and Conversions Great page explaining basic math with links to straight forward rotation conversion formulae.
• John H. Mathews, Bibliography for Quaternions.
• Quaternion powers on GameDev.net
• Andrew Hanson, Visualizing Quaternions home page.
• Representing Attitude with Euler Angles and Quaternions: A Reference, Technical report and Matlab toolbox summarizing all common attitude representations, with detailed equations and discussion on features of various methods.
• Johan E. Mebius, A matrix-based proof of the quaternion representation theorem for four-dimensional rotations., arXiv General Mathematics 2005.
• Johan E. Mebius, Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
• NUI Maynooth Department of Mathematics, Hamilton Walk.
• OpenGL:Tutorials:Using Quaternions to represent rotation
• David Erickson, Defence Research and Development Canada (DRDC), Complete derivation of rotation matrix from unitary quaternion representation in DRDC TR 2005-228 paper:[1]
• Alberto Martinez, University of Texas Department of History, "Negative Math, How Mathematical Rules Can Be Positively Bent", [2]
• D. Stahlke, Quaternions in Classical Mechanics (PDF)
• Morier-Genoud, Sophie, and Valentin Ovsienko. Well, Papa, can you multiply triplets? Describes how the quaternions can be made into a skew-commutative algebra graded by Z/2×Z/2×Z/2.

[edit] Software

• Euler Quaternion Pro A free GUI based utility that converts Euler angles to Quaternions around X,Y and Z (roll, pitch and yaw) axis and performs conjugate, addition, subtraction, multiplication, great circle interpolation operations on converted Quaternions.
• Quaternion Calculator [Java]
• Quaternion Toolbox for Matlab
• Boost library support for Quaternions in C++
• Mathematics of flight simulation >Turbo-PASCAL software for quaternions, Euler angles and Extended Euler angles

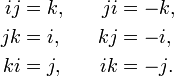
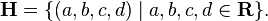
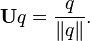
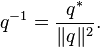
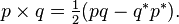
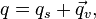
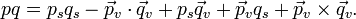
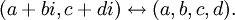
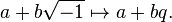
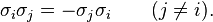
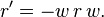
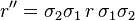
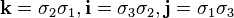
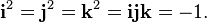
v • d • e Number systems Basic Natural numbers () · Integers () · Rational numbers () · Irrational numbers · Real numbers () · Imaginary numbers () · Complex numbers () · Algebraic numbers () · Transcendental numbers · Quaternions () · Octonions () · Sedenions () · Cayley–Dickson construction · Split-complex numbers Complex extensions Bicomplex numbers · Biquaternions · Split-quaternions · Tessarines · Hypercomplex numbers · Musean hypernumbers · Superreal numbers · Hyperreal numbers · Supernatural numbers · Surreal numbers Other extensions Dual numbers · Transfinite numbers · Extended real numbers · Cardinal numbers · Ordinal numbers · p-adic numbers