Simplex algorithm

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In mathematical optimization theory, the simplex algorithm, created by the American mathematician George Dantzig in 1947, is a popular algorithm for numerical solution of the linear programming problem. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the century.[1]

An unrelated, but similarly named method is the Nelder-Mead method or downhill simplex method due to Nelder & Mead (1965) and is a numerical method for optimizing many-dimensional unconstrained problems, belonging to the more general class of search algorithms.

In both cases, the method uses the concept of a simplex, which is a polytope of N + 1 vertices in N dimensions: a line segment in one dimension, a triangle in two dimensions, a tetrahedron in three-dimensional space and so forth.

Contents

[edit] Overview

Further information: Linear programming
A system of linear inequalities defines a polytope as a feasible region. The simplex algorithm begins at a starting vertex and moves along the edges of the polytope until it reaches the vertex of the optimum solution.

Consider a linear programming problem,

maximize \mathbf{c}^{T} \mathbf{x}
subject to \mathbf{A}\mathbf{x} \le \mathbf{b}, \, \mathbf{x} \ge 0.

In geometric terms, each inequality specifies a half-space in n-dimensional Euclidean space, and their intersection is the set of all feasible values the variables can take. The region is either empty, unbounded, or a convex polytope.

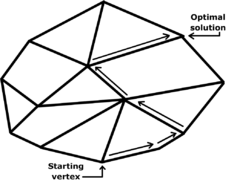
The set of points where the objective function obtains a given value v is defined by the hyperplane cTx = v. We are looking for the largest v such that the hyperplane still intersects the feasible region. As v increases, the hyperplanes translates in the direction of the vector c. Intuitively, and indeed it can be shown by convexity, the last hyperplane to intersect the feasible region will either just graze a vertex of the polytope, or a whole edge or face. In the latter two cases, it is still the case that the endpoints of the edge or face will achieve the optimum value. Thus, the optimum value will always be achieved on one of the vertices of the polytope.

The simplex algorithm leverages this insight by rewriting the problem so that one of the vertices of the (possibly unbounded) polytope is easy to find, or it is revealed that the problem is infeasible. Then, the algorithm walks along edges of the polytope to vertices with higher objective function value until a local maximum is reached, or the problem is revealed to be unbounded. By convexity, a local maximum is also a global maximum, so the solution has been found. Usually there are more than one adjacent vertices which improve the objective function, so a pivot rule must be specified to determine which vertex to pick. The selection of this rule has a great impact on the runtime of the algorithm.

In 1972, Klee and Minty[2] gave an example of a linear programming problem in which the polytope P is a distortion of an n-dimensional cube. They showed that the simplex method as formulated by Dantzig visits all 2n vertices before arriving at the optimal vertex. This shows that the worst-case complexity of the algorithm is exponential time. Since then it has been shown that for almost every deterministic rule there is a family of simplices on which it performs badly. It is an open question if there is a pivot rule with polynomial time, or even sub-exponential worst-case complexity.

Nevertheless, the simplex method is remarkably efficient in practice. It has been known since the 1970s that it has polynomial-time average-case complexity under various distributions. These results on "random" matrices still didn't quite capture the desired intuition that the method works well on "typical" matrices. In 2001 Spielman and Teng introduced the notion of smoothed complexity to provide a more realistic analysis of the performance of algorithms.[3]

Other algorithms for solving linear programming problems are described in the linear programming article.

[edit] Implementation

The simplex algorithm requires the linear programming problem to be in augmented form. The problem can then be written as follows in matrix form:

Maximize Z in:
\begin{bmatrix} 1 & -\mathbf{c}^T & 0 \\ 0 & \mathbf{A} & \mathbf{I} \end{bmatrix} \begin{bmatrix} Z \\ \mathbf{x} \\ \mathbf{x}_s \end{bmatrix} = \begin{bmatrix} 0 \\ \mathbf{b} \end{bmatrix}
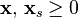
\mathbf{x}, \, \mathbf{x}_s \ge 0

where x are the variables from the standard form, xs are the introduced slack variables from the augmentation process, c contains the optimization coefficients, A and b describe the system of constraint equations, and Z is the variable to be maximized.

Suppose in the standard form of the problem there are n variables and m constraints, not counting the n nonnegativity constraints. Generally, a vertex of the simplex corresponds to making n of the m+n total constraints tight, while adjacent vertices share n-1 tight constraints. There is a little subtlety when such a point in n-space does not fall in feasible region. Ignoring that, in the augmented form, this corresponds to setting m of the m+n variables (n original and m slack) to 0. We call such a setting of the variables a basic solution. The m variables which are purposely set to 0 are called the nonbasic variables. We can then solve for the remaining n constraints, called the basic variables, which will be uniquely determined, as we will be careful not to step out of the feasible region.

The simplex algorithm begins by finding a basic feasible solution. At each step, one basic and one nonbasic variable are chosen according to the pivot rule, and their roles are switched.

[edit] Matrix form of the simplex algorithm

At any iteration of the simplex algorithm, the tableau will be of this form:

\begin{bmatrix} 1 & \mathbf{c}_B^T \mathbf{B}^{-1}\mathbf{A} -\mathbf{c}^T & \mathbf{c}_B^T \mathbf{B}^{-1} \\ 0 & \mathbf{B}^{-1}\mathbf{A} & \mathbf{B}^{-1} \end{bmatrix} \begin{bmatrix} Z \\ \mathbf{x} \\ \mathbf{x}_s \end{bmatrix} = \begin{bmatrix} \mathbf{c}_B^T \mathbf{B}^{-1} \mathbf{b} \\ \mathbf{B}^{-1}\mathbf{b} \end{bmatrix}

where \mathbf{c}_B are the coefficients of basic variables in the c-matrix; and B consists of the columns of [\mathbf{A} \, \mathbf{I}] corresponding to the basic variables.

It is worth noting that B and \mathbf{c}_B are the only variables in this equation (except Z and x of course). Everything else is constant throughout the algorithm.

[edit] Algorithm

  • Choose a basic feasible solution (BF) as shown above
This implies that B is the identity matrix, and \mathbf{c}_B is a zero-vector.
  • While nonoptimal solution:
    • Determine direction of highest gradient
    Choose the variable associated with the coefficient in \mathbf{c}_B^{T} \mathbf{B}^{-1}\mathbf{A} -\mathbf{c}^{T} that has the highest negative magnitude. This nonbasic variable, which we call the entering basic, will be increased to help maximize the problem.
    • Determine maximum step length
    Use the \begin{bmatrix} \mathbf{B}^{-1}\mathbf{A} & \mathbf{B}^{-1} \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ \mathbf{x}_s \end{bmatrix} = \mathbf{B}^{-1}\mathbf{b} subequation to determine which basic variable reaches zero first when the entering basic is increased. This variable, which we call the leaving basic then becomes nonbasic. This operation only involves a single division for each basic variable, since the existing basic-variables occur diagonally in the tableau.
    • Rewrite problem
    Modify B and \mathbf{c}_B to account for the new basic variables. This will automatically make the tableau diagonal for the existing and new basic variables.
    • Check for improvement
    Repeat procedure until no further improvement is possible, meaning all the coefficients of \mathbf{c}_B^{T} \mathbf{B}^{-1}\mathbf{A} -\mathbf{c}^{T} are positive. Procedure is also terminated if all coefficients are zero, and the algorithm has walked in a circle and revisited a previous state.

[edit] Implementation

The tableau form used above to describe the algorithm lends itself to an immediate implementation in which the tableau is maintained as a rectangular (m+1)-by-(m+n+1) array. It is straightforward to avoid storing the m explicit columns of the identity matrix that will occur within the tableau by virtue of B being a subset of the columns of [\mathbf{A} \, \mathbf{I}]. This implementation is referred to as the standard simplex method. The storage and computation overhead are such that the standard simplex method is a prohibitively expensive approach to solving large linear programming problems.

In each simplex iteration, the only data required are the first row of the tableau, the (pivotal) column of the tableau corresponding to the entering variable and the right-hand-side. The latter can be updated using the pivotal column and the first row of the tableau can be updated using the (pivotal) row corresponding to the leaving variable. Both the pivotal column and pivotal row may be computed directly using the solutions of linear systems of equations involving the matrix B and a matrix-vector product using A. These observations motivate the revised simplex method, for which implementations are distinguished by their invertible representation of B.

In large linear programming problems A is typically a sparse matrix and, when the resulting sparsity of B is exploited when maintaining its invertible representation, the revised simplex method is a vastly more efficient solution procedure than the standard simplex method. Commercial simplex solvers are based on the primal (or dual) revised simplex method.

[edit] Common implementations of the revised simplex method

[edit] See also

Sister project The Wikibook Operations Research has a page on the topic of

[edit] References

  1. ^ Computing in Science and Engineering, volume 2, no. 1, 2000
  2. ^ Greenberg, cites: V. Klee and G.J. Minty. "How Good is the Simplex Algorithm?" In O. Shisha, editor, Inequalities, III, pages 159–175. Academic Press, New York, NY, 1972
  3. ^ Spielman, Daniel; Teng, Shang-Hua (2001), "Smoothed analysis of algorithms: why the simplex algorithm usually takes polynomial time", Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing, ACM, pp. 296–305, doi:10.1145/380752.380813, arΧiv:cs/0111050, ISBN 978-1-58113-349-3 

[edit] Further reading

  • Greenberg, Harvey J., Klee-Minty Polytope Shows Exponential Time Complexity of Simplex Method University of Colorado at Denver (1997) PDF download
  • Frederick S. Hillier and Gerald J. Lieberman: Introduction to Operations Research, 8th edition. McGraw-Hill. ISBN 0-07-123828-X
  • Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 29.3: The simplex algorithm, pp.790–804.
  • Hamdy A. Taha: Operations Research: An Introduction, 8th ed., Prentice Hall, 2007. ISBN 0-13-188923-0
  • Richard B. Darst: Introduction to Linear Programming: Applications and Extensions

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Simplex_algorithm"
Personal tools