Cauchy distribution

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Cauchy-Lorentz
Probability density function
Probability density function for the Cauchy distribution
The green line is the standard Cauchy distribution
Cumulative distribution function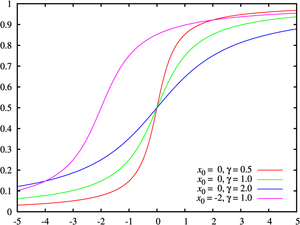
Cumulative distribution function for the Cauchy distribution
Colors match the pdf above
Parameters x_0\! location (real)
\gamma > 0\! scale (real)
Support x \in (-\infty; +\infty)\!
Probability density function (pdf) \frac{1}{\pi\gamma\,\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \!
Cumulative distribution function (cdf) \frac{1}{\pi} \arctan\left(\frac{x-x_0}{\gamma}\right)+\frac{1}{2}
Mean not defined
Median x0
Mode x0
Variance not defined
Skewness not defined
Excess kurtosis not defined
Entropy \ln(4\,\pi\,\gamma)\!
Moment-generating function (mgf) not defined
Characteristic function \exp(x_0\,i\,t-\gamma\,|t|)\!

The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz,  is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as a Lorentz distribution, or a Lorentz(ian) function or the Breit–Wigner distribution.

Its importance in physics is due to it being the solution to the differential equation describing forced resonance. In spectroscopy, it is the description of the line shape of spectral lines which are subject to homogeneous broadening in which all atoms interact in the same way with the frequency range contained in the lineshape. Many mechanisms cause homogeneous broadening, most notably collision broadening.

Contents

[edit] Characterization

[edit] Probability density function

The Cauchy distribution has the probability density function (pdf)

\begin{align} f(x; x_0,\gamma)&= \frac{1}{\pi\gamma \left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \\[0.5em] &= { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right] \end{align}

where x0 is the location parameter, specifying the location of the peak of the distribution, and γ is the scale parameter which specifies the half-width at half-maximum (HWHM). The amplitude of the above Lorentzian function is given by

\text{Amplitude (or height)} = \frac{1}{\pi\gamma}

In physics, a three-parameter Lorentzian function is often used, as follows:

\begin{align} f(x; x_0,\gamma,I) &= \frac{I}{\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \\[0.5em] &= { I }\left[ { \gamma^2 \over (x - x_0)^2 + \gamma^2 } \right] \end{align}

where I is the height of the peak. The special case when x0 = 0 and γ = 1 is called the standard Cauchy distribution with the probability density function

f(x; 0,1) = \frac{1}{\pi (1 + x^2)}. \!

[edit] Cumulative distribution function

The cumulative distribution function (cdf) is:

F(x; x_0,\gamma)=\frac{1}{\pi} \arctan\left(\frac{x-x_0}{\gamma}\right)+\frac{1}{2}

and the inverse cumulative distribution function of the Cauchy distribution is

F^{-1}(p; x_0,\gamma) = x_0 + \gamma\,\tan\left[\pi\,\left(p-\tfrac{1}{2}\right)\right].

[edit] Properties

The Cauchy distribution is an example of a distribution which has no mean, variance or higher moments defined. Its mode and median are well defined and are both equal to x0.

When U and V are two independent normally distributed random variables with expected value 0 and variance 1, then the ratio U/V has the standard Cauchy distribution.

If X1, …, Xn are independent and identically distributed random variables, each with a standard Cauchy distribution, then the sample mean (X1 + … + Xn)/n has the same standard Cauchy distribution (the sample median, which is not affected by extreme values, can be used as a measure of central tendency). To see that this is true, compute the characteristic function of the sample mean:

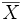\phi_{\overline{X}}(t) = \mathrm{E}\left(e^{i\,\overline{X}\,t}\right) \,\!

where \overline{X} is the sample mean. This example serves to show that the hypothesis of finite variance in the central limit theorem cannot be dropped. It is also an example of a more generalized version of the central limit theorem that is characteristic of all Lévy skew alpha-stable distributions, of which the Cauchy distribution is a special case.

The Cauchy distribution is an infinitely divisible probability distribution. It is also a strictly stable distribution.

The standard Cauchy distribution coincides with the Student's t-distribution with one degree of freedom.

The location-scale family to which the Cauchy distribution belongs is closed under linear fractional transformations with real coefficients. In this connection, see also McCullagh's parametrization of the Cauchy distributions.

[edit] Characteristic function

Let X denote a Cauchy distributed random variable. The characteristic function of the Cauchy distribution is given by

\phi_x(t; x_0,\gamma) = \mathrm{E}(e^{i\,X\,t}) = \exp(i\,x_0\,t-\gamma\,|t|). \!

[edit] Why the mean of the Cauchy distribution is undefined

If a probability distribution has a density function f(x) then the mean is

\int_{-\infty}^\infty x f(x)\,dx. \qquad\qquad (1)\!

The question is now whether this is the same thing as

\int_0^\infty x f(x)\,dx-\int_{-\infty}^0 |{x}| f(x)\,dx.\qquad\qquad (2) \!

If at most one of the two terms in (2) is infinite, then (1) is the same as (2). But in the case of the Cauchy distribution, both the positive and negative terms of (2) are infinite. This means (2) is undefined. Moreover, if (1) is construed as a Lebesgue integral, then (1) is also undefined, since (1) is then defined simply as the difference (2) between positive and negative parts.

However, if (1) is construed as an improper integral rather than a Lebesgue integral, then (2) is undefined, and (1) is not necessarily well-defined. We may take (1) to mean

\lim_{a\to\infty}\int_{-a}^a x f(x)\,dx, \!

and this is its Cauchy principal value, which is zero, but we could also take (1) to mean, for example,

\lim_{a\to\infty}\int_{-2a}^a x f(x)\,dx, \!

which is not zero, as can be seen easily by computing the integral.

Various results in probability theory about expected values, such as the strong law of large numbers, will not work in such cases.

[edit] Why the second moment of the Cauchy distribution is infinite

Without a defined mean, it is impossible to consider the variance or standard deviation of a standard Cauchy distribution, as these are defined with respect to the mean. But the second moment about zero can be considered. It turns out to be infinite:

\mathrm{E}(X^2) \propto \int_{-\infty}^{\infty} {x^2 \over 1+x^2}\,dx = \int_{-\infty}^{\infty} dx - \int_{-\infty}^{\infty} {1 \over 1+x^2}\,dx = \int_{-\infty}^{\infty} dx -\pi = \infty. \!

[edit] Related distributions

[edit] Relativistic Breit-Wigner distribution

In nuclear and particle physics, the energy profile of a resonance is described by the relativistic Breit-Wigner distribution, while the Cauchy distribution is the (non-relativistic) Breit–Wigner distribution.

[edit] See also

[edit] External links


v • d • e
Probability distributions
 
Continuous univariate supported on the whole real line (-∞,∞)
Retrieved from "http://en.wikipedia.org/wiki/Cauchy_distribution"
Personal tools