Digital sundial

From Wikipedia, the free encyclopedia

Jump to: navigation, search

A digital sundial is a clock that indicates the current time with numerals formed by the sunlight striking it. Like a classical sundial, the device is purely passive and contains no moving parts. It uses no electricity nor other artificial sources of energy. The digital display changes as the sun advances in its daily course.

Contents

[edit] Technique

There are two basic types of digital sundials. One construction uses optical waveguides, while the other is inspired by fractal geometry.

[edit] Optical fiber sundial

Sunlight enters into the device through a slit and moves as the sun advances. The sun's rays shine on ten linearly distributed sockets of optical waveguides that transport the light to a seven-segment display. Each socket fiber is connected to a few segments forming the digit corresponding to the position of the sun.[1]

[edit] Fractal sundial

Digital sundial in the sundial parc in Genk, Flanders in Belgium.

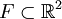The theoretical basis for the other construction comes from fractal geometry.[2] For the sake of simplicity we describe a two-dimensional (planar) version. Let Lθ denote a straight line passing by the origin of a Cartesian coordinate system and making angle \theta\in [0,\pi) with the x-axis. For any F\subset \mathbb{R}^2 define projθF to be the perpendicular projection of F on the line Lθ.

[edit] Theorem

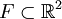Let G_\theta \subset L_\theta, \theta\in[0,\pi) be a family of any sets such that \bigcup_\theta G_\theta is a measurable set in the plane. Then there exists a set F\subset \mathbb{R}^2 such that

  • G_\theta \subset \mathrm{proj}_\theta F ;
  • the measure of the set (\mathrm{proj}_\theta F)\setminus G_\theta is zero for almost all \theta\in[0,\pi).

Roughly speaking, there exists a set with prescribed projections in almost all directions. This theorem can be generalized to three-dimensional space. Typically, for a non-trivial choice of the family Gθ, the set F described above is a fractal.

[edit] Towards application

It follows that, theoretically, it is possible to build a set of masks that produce shadows in the form of digits such that the display changes as the sun moves. This is the fractal sundial.

The theorem was proved in 1987 by Kenneth Falconer. Four years later it was described in Scientific American by Ian Stewart. The first prototype of the device was constructed in 1994. In 1998 for the first time a fractal sundial was installed in a public place (Genk, Belgium).[3] There exist window and tabletop versions as well.[4]

[edit] References

  1. ^ US patent belongs to HinesLab Inc. (USA) [1]
  2. ^ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd.. xxv. ISBN 0-470-84862-6. 
  3. ^ Sundial park in Genk, Belgium [2]
  4. ^ US and German patent belongs to Digital Sundials International [3]
Retrieved from "http://en.wikipedia.org/wiki/Digital_sundial"
Personal tools
Languages