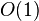Vickrey auction

From Wikipedia, the free encyclopedia

Jump to: navigation, search

A Vickrey auction is a type of sealed-bid auction, where bidders submit written bids without knowing the bid of the other people in the auction. The highest bidder wins, but the price paid is the second-highest bid. The auction was created by William Vickrey. This type of auction is strategically similar to an English auction, and gives bidders an incentive to bid their true value.

Vickrey's original paper considered only auctions where a single, indivisible good is being sold. In this case, the terms Vickrey auction and second-price sealed-bid auction are equivalent, and are used interchangeably. When multiple identical units (or a divisible good) are being sold in a single auction, the most obvious generalization is to have all winning bidders pay the amount of the highest non-winning bid. This is known as a uniform price auction. The uniform-price auction does not, however, result in bidders bidding their true valuations as they do in a second-price auction unless each bidder has demand for only a single unit.

A generalization of the Vickrey auction that maintains the incentive to bid truthfully is known as the Vickrey-Clarke-Groves (VCG) mechanism. The idea in VCG is that each player in the auction pays the opportunity cost that their presence introduces to all the other players. For example, suppose that we want to auction two apples, and we have three bidders. Bidder A wants one apple and bids $5 for that apple. Bidder B wants one apple and is willing to pay $2 for it. Bidder C wants two apples and is willing to pay $6 to have both of them, but is uninterested in buying only one without the other. First, we decide the outcome of the auction by maximizing bids: the apples go to bidder A and bidder B. Next, to decide payments, we consider the opportunity cost that each bidder imposed on the rest of the bidders. Currently, B has a utility of $2. If bidder A had not been present, C would have won, and had a utility of $6, so A pays $6-$2 = $4. For the payment of bidder B: currently A has a utility of $5 and C has a utility of 0. If bidder B had been absent, C would have won and had a utility of $6, so B pays $6-$5 = $1. The outcome is identical whether or not bidder C participates, so C does not need to pay anything.

Vickrey auctions are much studied in economic literature, but are not particularly common in practice. One market in which they have been used is stamp collecting. eBay's system of proxy bidding is similar, but not identical, to a Vickrey auction. A slight generalized variant of a Vickrey auction, named generalized second-price auction, which is different from the VCG mechanism, is known to be used in Google's and Yahoo!'s online advertisement programmes.[1][2]

Contents

[edit] Properties

[edit] Self-revelation/Incentive compatibility

In a Vickrey auction with independent private values (IPV) each bidder maximizes his or her expected utility by bidding (revealing) his or her true valuation.

[edit] Ex-post efficiency

A Vickrey auction is ex post efficient (the winner is the bidder with the highest valuation) under the most general circumstances; it thus provides a baseline model against which the efficiency properties of other types of auctions can be posited.

[edit] Weaknesses

Despite the Vickrey auction's strengths, it has shortcomings:

  • It does not allow for Price discovery, that is, discovery of the market price if the buyers are unsure of their own valuations, without sequential auctions.
  • Sellers may use shill bids to increase profit.
  • In iterated Vickrey auctions, the strategy of revealing true valuations is no longer dominant.[vague]

The Vickrey-Clarke-Groves (VCG) mechanism has the additional shortcomings:

  • It is vulnerable to collusion by losing bidders.
  • It is vulnerable to shill bidding with respect to the buyers.
  • It does not necessarily maximize seller revenues; seller revenues may even be zero in VCG auctions. If the purpose of holding the auction is to maximize profit for the seller rather than just allocate resources among buyers, then VCG may be a poor choice.
  • The seller's revenues are non-monotonic with regard to the sets of bidders and offers.

The non-monotonicity of seller's revenues with respect to bids can be shown by the following example. Consider 3 bidders A, B, and C, and two homogeneous items bid upon, Y and Z. A wants both items and bids $2 for the package of Y and Z. B and C both bid $2 each for a single item (bid $2 for Y or Z), as they really want one item but don't care if they have the second. Now, Y and Z are allocated to B and C, but the price is $0, as can be found by removing either B or C respectively. If C bid $0 instead of $2, then the seller would make $2 instead of $0. Because the seller's revenue can also go up when bids are increased, the seller's revenues are non-monotonic with respect to bids.

[edit] Proof of Optimality of Truthful Bidding

The optimal strategy in a Vickrey auction with a single, indivisible item is for each bidder to bid their true value of the item.[3]

Let vi be bidder i's value for the item. Let bi be bidder i's bid for the item.

The payoff for bidder i is 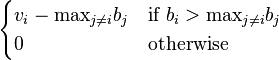\begin{cases} v_i-\mbox{max}_{j\neq i} b_j & \mbox{if } b_i > \mbox{max}_{j\neq i} b_j \\ 0 & \mbox{otherwise} \end{cases}

The strategy of overbidding is dominated by bidding truthfully. Assume that bidder i bids bi > vi.

If \mbox{max}_{j\neq i} b_j < v_i then the bidder would win the item with a truthful bid as well as an overbid. The bid's amount does not change the payoff so the two strategies have equal payoffs in this case.

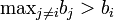If \mbox{max}_{j\neq i} b_j > b_i then the bidder would lose the item either way so the strategies have equal payoffs in this case.

If v_i < \mbox{max}_{j\neq i} b_j < b_i then only the strategy of overbidding would win the auction. The payoff would be negative for the strategy of overbidding because they paid more than their value of the item, while the payoff for a truthful bid would be zero. Thus the strategy of bidding higher than one's true valuation is dominated by the strategy of truthfully bidding.

The strategy of underbidding is dominated by bidding truthfully. Assume that bidder i bids bi < vi.

If 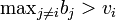\mbox{max}_{j\neq i} b_j > v_i then the bidder would lose the item with a truthful bid as well as an overbid, so the strategies have equal payoffs for this case.

If 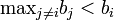\mbox{max}_{j\neq i} b_j < b_i then the bidder would win the item either way so the strategies have equal payoffs in this case.

If b_i < \mbox{max}_{j\neq i} b_j < v_i then only the strategy of truthfully bidding would win the auction. The payoff for the truthful strategy would be payoff as they paid less than their value of the item, while the payoff for an underbid bid would be zero. Thus the strategy of underbidding is dominated by the strategy of truthfully bidding.

Truthful bidding dominates the other possible strategies (underbidding and overbidding) so it is an optimal strategy.

[edit] Use in U.S. Treasury securities

U.S. Treasury securities are auctioned in competitive bidding under rules that are very similar to a Vickrey auction.[citation needed]

[edit] Use in network routing

In network routing, VCG mechanisms are a family of payment schemes based on the added value concept. The basic idea of a VCG mechanism in network routing is to pay the owner of each link or node (depending on the network model) that is part of the solution, its declared cost plus its added value. In many routing problems, this mechanism is not only strategyproof, but also the minimum among all strategyproof mechanisms.

In the case of network flows, Unicast or Multicast, a minimum cost flow (MCF) in graph G is calculated based on the declared costs dk of each of the links and payment is calculated as follows:

Each link (or node) \scriptstyle e_k in the MCF is paid

pk = dk + MCF(G − ek) − MCF(G),

where MCF(G) indicates the cost of the minimum cost flow in graph G and G-ek indicates graph G without the link ek. Links not in the MCF are paid nothing. This routing problem is one of the cases for which VCG is strategyproof and minimum.

In 2004, it was shown that the expected VCG overpayment of an Erdös-Renyi random graph with n nodes and edge probability p, \scriptstyle G \in G(n, p) approaches

\frac{p}{2-p}

as n, approaches 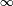\scriptstyle \infty , for n p = \omega(\sqrt{n \log n}). Prior to this result, it was known that VCG overpayment in G(n, p) is

\Omega\left(\frac{1}{np}\right)

and

O(1)\,

with high probability given

np=\omega(\log n).\,

[edit] External links

[edit] References

  • Vijay Krishna, Auction Theory, Academic Press, 2002.
  • Peter Cramton, Yoav Shoham, Richard Steinberg (Eds), Combinatorial Auctions, MIT Press, 2006, Chapter 1. ISBN 0-262-03342-9.
  • Paul Milgrom, Putting Auction Theory to Work, Cambridge University Press, 2004.

[edit] Notes

  1. ^ Benjamin Edelman, Michael Ostrovsky, and Michael Schwarz: "Internet Advertising and the Generalized Second-Price Auction: Selling Billions of Dollars Worth of Keywords". American Economic Review 97(1), 2007 pp 242-259.
  2. ^ Hal R. Varian: "Position Auctions". International Journal of Industrial Organization, 2006, doi:10.1016/j.ijindorg.2006.10.002 .
  3. ^ von Ahn, Luis (2008-09-30). "Auctions" (PDF). 15-396: Science of the Web Course Notes. Carnegie Mellon University. http://www.scienceoftheweb.org/15-396/lectures/lecture09.pdf. Retrieved on 2008-11-06. 
Retrieved from "http://en.wikipedia.org/wiki/Vickrey_auction"
Personal tools