Rankine cycle

From Wikipedia, the free encyclopedia

Jump to: navigation, search

The Rankine cycle is a thermodynamic cycle which converts heat into work. The heat is supplied externally to a closed loop, which usually uses water as the working fluid. This cycle generates about 80% of all electric power used throughout the world.[1], including virtually all solar thermal, biomass, coal and nuclear power plants. It is named after William John Macquorn Rankine, a Scottish polymath.

Contents

[edit] Description

Physical layout of the four main devices used in the Rankine cycle

A Rankine cycle describes a model of the operation of steam heat engines most commonly found in power generation plants. Common heat sources for power plants using the Rankine cycle are coal, natural gas, oil, and nuclear.

The Rankine cycle is sometimes referred to as a practical Carnot cycle as, when an efficient turbine is used, the TS diagram will begin to resemble the Carnot cycle. The main difference is that a pump is used to pressurize liquid instead of gas. This requires about 100 times less energy[citation needed] than that compressing a gas in a compressor (as in the Carnot cycle).

The efficiency of a Rankine cycle is usually limited by the working fluid. Without the pressure going super critical the temperature range the cycle can operate over is quite small, turbine entry temperatures are typically 565°C (the creep limit of stainless steel) and condenser temperatures are around 30°C. This gives a theoretical Carnot efficiency of around 63% compared with an actual efficiency of 42% for a modern coal-fired power station. This low turbine entry temperature (compared with a gas turbine) is why the Rankine cycle is often used as a bottoming cycle in combined cycle gas turbine power stations.

The working fluid in a Rankine cycle follows a closed loop and is re-used constantly. The water vapor and entrained droplets often seen billowing from power stations is generated by the cooling systems (not from the closed loop Rankine power cycle) and represents the waste heat that could not be converted to useful work. Note that cooling towers operate using the latent heat of vaporization of the cooling fluid. The white billowing clouds that form in cooling tower operation are the result of water droplets which are entrained in the cooling tower airflow; it is not, as commonly thought, steam. While many substances could be used in the Rankine cycle, water is usually the fluid of choice due to its favorable properties, such as nontoxic and unreactive chemistry, abundance, and low cost, as well as its thermodynamic properties.

One of the principal advantages it holds over other cycles is that during the compression stage relatively little work is required to drive the pump, due to the working fluid being in its liquid phase at this point. By condensing the fluid to liquid, the work required by the pump will only consume approximately 1% to 3% of the turbine power and so give a much higher efficiency for a real cycle. The benefit of this is lost somewhat due to the lower heat addition temperature. Gas turbines, for instance, have turbine entry temperatures approaching 1500°C. Nonetheless, the efficiencies of steam cycles and gas turbines are fairly well matched.

[edit] Processes of the Rankine cycle

Ts diagram of a typical Rankine cycle operating between pressures of 0.06bar and 50bar

There are four processes in the Rankine cycle, each changing the state of the working fluid. These states are identified by number in the diagram to the right.

  • Process 1-2: The working fluid is pumped from low to high pressure, as the fluid is a liquid at this stage the pump requires little input energy.
  • Process 2-3: The high pressure liquid enters a boiler where it is heated at constant pressure by an external heat source to become a dry saturated vapor.
  • Process 3-4: The dry saturated vapor expands through a turbine, generating power. This decreases the temperature and pressure of the vapor, and some condensation may occur.
  • Process 4-1: The wet vapor then enters a condenser where it is condensed at a constant pressure and temperature to become a saturated liquid. The pressure and temperature of the condenser is fixed by the temperature of the cooling coils as the fluid is undergoing a phase-change.

In an ideal Rankine cycle the pump and turbine would be isentropic, i.e., the pump and turbine would generate no entropy and hence maximize the net work output. Processes 1-2 and 3-4 would be represented by vertical lines on the Ts diagram and more closely resemble that of the Carnot cycle. The Rankine cycle shown here prevents the vapor ending up in the superheat region after the expansion in the turbine [1], which reduces the energy removed by the condensers.

[edit] Variables

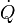\dot{Q} Heat flow rate to or from the system (energy per unit time)
\dot{m} Mass flow rate (mass per unit time)
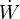\dot{W} Mechanical power consumed by or provided to the system (energy per unit time)
ηtherm Thermodynamic efficiency of the process (net power output per heat input, dimensionless)
ηpump,ηturb Isentropic efficiency of the compression (feed pump) and expansion (turbine) processes, dimensionless
h1,h2,h3,h4 The "specific enthalpies" at indicated points on the T-S diagram
h4s The final "specific enthalpy" of the fluid if the turbine were isentropic
p1,p2 The pressures before and after the compression process

[edit] Equations

Each of the first four equations[1] is easily derived from the energy and mass balance for a control volume. The fifth equation defines the thermodynamic efficiency of the cycle as the ratio of net power output to heat input. As the work required by the pump is often around 1% of the turbine work output, equation 5 can be simplified.

\frac{\dot{Q}_{\mathit{in}}} {\dot{m}} = h_3 - h_2

\frac{\dot{W}_{\mathit{pump}}} {\dot{m}} = h_2 - h_1 \approx \frac{v_1{\Delta}p}{\eta_{pump}} \approx \frac{v_1 (p_2 - p_1)}{\eta_{pump}}

\frac{\dot{Q}_{\mathit{out}}} {\dot{m}} = h_4 - h_1

\frac{\dot{W}_{\mathit{turbine}}} {\dot{m}} = h_3 - h_4 = (h_3 - h_{4s}) \times {\eta_{turb}}

\eta_{therm} = \frac{\dot{W}_{\mathit{turbine}}-\dot{W}_{\mathit{pump}}} {\dot{Q}_{\mathit{in}}} \approx \frac{\dot{W}_{\mathit{turbine}}} {\dot{Q}_{\mathit{in}}}

[edit] Real Rankine cycle (non-ideal)

Rankine cycle with superheat

In a real Rankine cycle, the compression by the pump and the expansion in the turbine are not isentropic. In other words, these processes are non-reversible and entropy is increased during the two processes. This somewhat decreases the power required by the pump and increases the power generated by the turbine.

In particular the efficiency of the steam turbine will be limited by water droplet formation. As the water condenses, water droplets hit the turbine blades at high speed causing pitting and erosion, gradually decreasing the life of turbine blades and efficiency of the turbine. The easiest way to overcome this problem is by superheating the steam. On the Ts diagram above, state 3 is above a two phase region of steam and water so after expansion the steam will be very wet. By superheating, state 3 will move to the right of the diagram and hence produce a dryer steam after expansion.

[edit] Variations of the basic Rankine cycle

Rankine cycle with reheat

The overall thermodynamic efficiency (of almost any cycle) can be increased by raising the average heat input temperature \left( \bar{T}_\mathit{in} = \frac{\int_2^3 T\,dQ}{Q_\mathit{in}} \right) of that cycle. Increasing the temperature of the steam into the superheat region is a simple way of doing this. There are also variations of the basic Rankine cycle which are designed to raise the thermal efficiency of the cycle in this way; two of these are described below.

[edit] Rankine cycle with reheat

In this variation, two turbines work in series. The first accepts vapor from the boiler at high pressure. After the vapor has passed through the first turbine, it re-enters the boiler and is reheated before passing through a second, lower pressure turbine. Among other advantages, this prevents the vapor from condensing during its expansion which can seriously damage the turbine blades, and improves the efficiency of the cycle.

[edit] Regenerative Rankine cycle

Regenerative Rankine cycle

The regenerative Rankine cycle is so named because after emerging from the condenser (possibly as a subcooled liquid) the working fluid is heated by steam tapped from the hot portion of the cycle. On the diagram shown, the fluid at 2 is mixed with the fluid at 4 (both at the same pressure) to end up with the saturated liquid at 7. The Regenerative Rankine cycle (with minor variants) is commonly used in real power stations.

Another variation is where 'bleed steam' from between turbine stages is sent to feedwater heaters to preheat the water on its way from the condenser to the boiler.

[edit] Organic Rankine Cycle

Main article: Organic Rankine Cycle

The organic Rankine cycle (ORC) uses an organic fluid such as n-pentane[2] or toluene[3] in place of water and steam. This allows use of lower-temperature heat sources, such as solar ponds, which typically operate at around 70–90 °C[4]. The efficiency of the cycle is much lower as a result of the lower temperature range, but this can be worthwhile because of the lower cost involved in gathering heat at this lower temperature. Alternatively, fluids can be used that have boiling points above water, and this may have thermodynamic benefits.

The Rankine cycle does not restrict the working fluid in its definition, so the inclusion of an "organic" cycle is simply a marketing concept that should not be regarded as a separate thermodynamic cycle.

v • d • e
Thermodynamic cycles
Cycles normally with
external combustion
Gas cycles without phasechange -
hot air engine cycles
Cycles with phasechange
Cycles normally with
internal combustion
Cycle mixing
Not categorized

[edit] References

  1. ^ Steam engine
  2. ^ Canada, Scott; G. Cohen, R. Cable, D. Brosseau, and H. Price (2004-10-25). "Parabolic Trough Organic Rankine Cycle Solar Power Plant" (in English). 2004 DOE Solar Energy Technologies (Denver, Colorado: US Department of Energy NREL). http://www.nrel.gov/csp/troughnet/pdfs/37077.pdf. Retrieved on 2009-03-17. 
  3. ^ Batton, Bill (2000-06-18). "Organic Rankine Cycle Engines for Solar Power" (in English). Solar 2000 conference. Barber-Nichols, Inc.. http://www.nrel.gov/csp/troughnet/pdfs/batton_orc.pdf. Retrieved on 2009-03-18. 
  4. ^ Nielsen et al, 2005, Proc. Int. Solar Energy Soc.

[edit] External links

v • d • e
Electricity generation
Concepts
Sources
Biomass · Geothermal · Hydro · Ocean · Solar · Wind
Technology
Distribution
Policies
Categories: Electricity distribution · Electricity economics · Power station technology · Portals: Energy · Sustainable development
Retrieved from "http://en.wikipedia.org/wiki/Rankine_cycle"
Personal tools