Currying

From Wikipedia, the free encyclopedia

Jump to: navigation, search
This article is about the function transformation technique. For the general variety of spicy dishes from Asia, see Curry. For the electrical retailer in the United Kingdom, see Currys.

In computer science, currying, invented by Moses Schönfinkel and Gottlob Frege, and independently by Haskell Curry,[1] is the technique of transforming a function that takes multiple arguments (or more accurately an n-tuple as argument) in such a way that it can be called as a chain of functions each with a single argument.

Contents

[edit] Nomenclature

The name "currying", coined by Christopher Strachey in 1967, is a reference to logician Haskell Curry. An alternative name, Schönfinkelisation, has been proposed. [2]

[edit] Definition

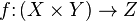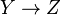Given a function f of type f \colon (X \times Y) \to Z , then currying it makes a function \mbox{curry}(f) \colon X \to (Y \to Z) . That is, curry(f) takes an argument of type X and returns a function of type Y \to Z . Uncurrying is the reverse transformation.

Intuitively, currying says "if you fix some arguments, you get a function of the remaining arguments". For example, if function div stands for the curried form of the division operation x / y, then div with the parameter x fixed at 1 is another function: the same as the function inv that returns the multiplicative inverse of its argument, defined by inv(y) = 1 / y.

The practical motivation for currying is that very often the functions obtained by supplying some but not all of the arguments to a curried function (often called partial application) are useful; for example, many languages have a function or operator similar to plus_one. Currying makes it easy to define these functions.

Some programming languages have built-in syntactic support for currying, where what looks like a multi-argument function is actually syntactic sugar for the function in curried form; notable examples are ML and Haskell, where in both cases all functions have exactly one argument. This convention is also used in lambda calculus, where functions also all have exactly one argument, and multi-argument functions are usually represented in curried form.

Any language that supports closures can be used to write curried functions.

[edit] Mathematical view

In theoretical computer science, currying provides a way to study functions with multiple arguments in very simple theoretical models such as the lambda calculus in which functions only take a single argument.

When viewed in a set-theoretic light, currying becomes the theorem that the set A^{B\times C} of functions from B\times C to A, and the set (AB)C of functions from C to the set of functions from B to A, are isomorphic.

In category theory, currying can be found in the universal property of an exponential object, which gives rise to the following adjunction in cartesian closed categories: There is a natural isomorphism between the morphisms from a binary product 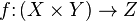f \colon (X \times Y) \to Z and the morphisms to an exponential object g \colon X \to Z^Y . In other words, currying is the statement that product and Hom are adjoint functors; this is the key property of being a Cartesian closed category.

Under the Curry-Howard correspondence, the existence of currying and uncurrying is equivalent to the logical theorem (A \and B) \to C \Leftrightarrow A \to (B \to C), as tuples (product type) corresponds to conjunction in logic, and function type corresponds to implication.

[edit] See also

[edit] Notes

  1. ^ (Barendregt 2000, p. 8)
  2. ^ I. Heim and A. Kratzer (1998). Semantics in Generative Grammar. Blackwell.

[edit] References

[edit] External links

Look up currying in Wiktionary, the free dictionary.
Retrieved from "http://en.wikipedia.org/wiki/Currying"
Personal tools