Vector calculus
From Wikipedia, the free encyclopedia
Vector calculus (or vector analysis) is a branch of mathematics concerned with differentiation and integration of vector fields. The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculus, which includes vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic, gravitational fields and fluid flow
Vector calculus was developed from quaternion analysis by J. Willard Gibbs and Oliver Heaviside near the end of the 19th century, and most of the notation and terminology was established by Gibbs and Wilson in their 1901 book, Vector Analysis.
[edit] Vector operations
Vector calculus studies various differential operators defined on scalar or vector fields, which are typically expressed in terms of the del operator ( ). The four most important operations in vector calculus are:
). The four most important operations in vector calculus are:
| Operation | Notation | Description | Domain/Range |
|---|---|---|---|
| Gradient |  |
Measures the rate and direction of change in a scalar field. | Maps scalar fields to vector fields. |
| Curl |  |
Measures the tendency to rotate about a point in a vector field. | Maps vector fields to vector fields. |
| Divergence |  |
Measures the magnitude of a source or sink at a given point in a vector field. | Maps vector fields to scalar fields. |
| Laplacian | 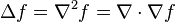 |
A composition of the divergence and gradient operations. | Maps scalar fields to scalar fields. |
A quantity called the Jacobian is useful for studying functions when both the domain and range of the function are multivariable, such as a change of variables during integration.
[edit] Theorems
Likewise, there are several important theorems related to these operators which generalize the fundamental theorem of calculus to higher dimensions:
| Theorem | Statement | Description |
|---|---|---|
| Gradient theorem | 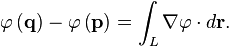 |
The line integral through a gradient (vector) field equals the difference in its scalar field at the endpoints of the curve. |
| Green's theorem |  |
The integral of the scalar curl of a vector field over some region in the plane equals the line integral of the vector field over the curve bounding the region. |
| Stokes' theorem | 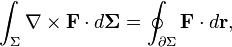 |
The integral of the curl of a vector field over a surface equals the line integral of the vector field over the curve bounding the surface. |
| Divergence theorem | 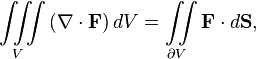 |
The integral of the divergence of a vector field over some solid equals the integral of the flux through the surface bounding the solid. |
The use of vector calculus may require the handedness of the coordinate system to be taken into account (see cross product and handedness for more detail). Most of the analytic results are easily understood, in a more general form, using the machinery of differential geometry, of which vector calculus forms a subset.
[edit] See also
- Vector calculus identities
- Irrotational vector field
- Solenoidal vector field
- Laplacian vector field
- Vector Analysis (Gibbs/Wilson)
[edit] References
- Michael J. Crowe (1994). A History of Vector Analysis : The Evolution of the Idea of a Vectorial System. Dover Publications; Reprint edition. ISBN 0-486-67910-1. (Summary)
- H. M. Schey (2005). Div Grad Curl and all that: An informal text on vector calculus. W. W. Norton & Company. ISBN 0-393-92516-1.
- J.E. Marsden (1976). Vector Calculus. W. H. Freeman & Company. ISBN 0-7167-0462-5.
- Chen-To Tai (1995). A historical study of vector analysis. Technical Report RL 915, Radiation Laboratory, University of Michigan.
[edit] External links
- Expanding vector analysis to a non-orthogonal space
- Vector Analysis: A Text-book for the Use of Students of Mathematics and Physics, (based upon the lectures of Willard Gibbs) by Edwin Bidwell Wilson, published 1902.

