Type theory

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general. In programming language theory, a branch of computer science, type theory can refer to the design, analysis and study of type systems, although some computer scientists limit the term's meaning to the study of abstract formalisms such as typed λ-calculi.

Bertrand Russell invented the first type theory in response to his discovery that Gottlob Frege's version of naive set theory was afflicted with Russell's paradox. This type theory features prominently in Whitehead and Russell's Principia Mathematica. It avoids Russell's paradox by first creating a hierarchy of types, then assigning each mathematical (and possibly other) entity to a type. Objects of a given type are built exclusively from objects of preceding types (those lower in the hierarchy), thus preventing loops.

Alonzo Church, inventor of the lambda calculus, developed a higher-order logic commonly called Church's Theory of Types, in order to avoid the Kleene-Rosser paradox afflicting the original pure lambda calculus. Church's type theory is a variant of the lambda calculus in which expressions (also called formulas or λ-terms) are classified into types, and the types of expressions restrict the ways in which they can be combined. In other words, it is a typed lambda calculus. Today many other such calculi are in use, including Per Martin-Löf's Intuitionistic type theory, Jean-Yves Girard's System F and the Calculus of Constructions. In typed lambda calculi, types play a role similar to that of sets in set theory.

Contents

[edit] Simple theory of types

The following system is Mendelson's (1997, 289–293) ST. The domain of quantification is partitioned into an ascending hierarchy of types, with all individuals assigned a type. Quantified variables range over only one type; hence the underlying logic is first-order logic. ST is "simple" (relative to the type theory of Principia Mathematica) primarily because all members of the domain and codomain of any relation must be of the same type.

There is a lowest type, whose individuals have no members and are members of the second lowest type. Individuals of the lowest type correspond to the urelements of certain set theories. Each type has a next higher type, analogous to the notion of successor in Peano arithmetic. While ST is silent as to whether there is a maximal type, a transfinite number of types poses no difficulty. These facts, reminiscent of the Peano axioms, make it convenient and conventional to assign a natural number to each type, starting with 0 for the lowest type. But type theory does not require a prior definition of the naturals.

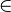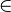The symbols peculiar to ST are primed variables and infix \in. In any given formula, unprimed variables all have the same type, while primed variables (x') range over the next higher type. The atomic formulas of ST are of two forms, x = y (identity) and y\in x'. The infix symbol \in suggests the intended interpretation, set membership.

All variables appearing in the definition of identity and in the axioms Extensionality and Comprehension, range over individuals of one of two consecutive types. Only unprimed (primed) variables, ranging over the "lower" ("higher") type, can appear to the left (right) of '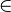\in'. The first-order formulation of ST rules out quantifying over types. Hence each pair of consecutive types requires its own axiom of Extensionality and of Comprehension, which is possible if Extensionality and Comprehension below are taken as axiom schemata "ranging over" types.

  • Identity, defined by x=y\leftrightarrow\forall z' [x\in z'\leftrightarrow y\in z'].
Let Φ(x) denote any first-order formula containing the free variable x.
Remark. Any collection of elements of the same type may form an object of the next higher type. Comprehension is schematic with respect to Φ(x) as well as to types.
Remark. Infinity is the only true axiom of ST and is entirely mathematical in nature. It asserts that R is a strict total order, with a domain identical to its codomain. If 0 is assigned to the lowest type, the type of R is 3. Infinity can be satisfied only if the (co)domain of R is infinite, thus forcing the existence of an infinite set. If relations are defined in terms of ordered pairs, this axiom requires a prior definition of ordered pair; the Kuratowski definition, adapted to ST, will do. The literature does not explain why the usual axiom of infinity (there exists an inductive set) of ZFC of other set theories could not be married to ST.

ST reveals how type theory can be made very similar to axiomatic set theory. Moreover, the more elaborate ontology of ST, grounded in what is now called the "iterative conception of set," makes for axiom (schemata) that are far simpler than those of conventional set theories, such as ZFC, with simpler ontologies. Set theories whose point of departure is type theory, but whose axioms, ontology, and terminology differ from the above, include New Foundations and Scott-Potter set theory.

[edit] History of type theory

This section requires expansion.

In 1908 Bertrand Russell in attempts to solve his famous antinomy concerning the set of all sets not in themselves, created Type Theory in hopes of working around these paradoxes. His young protege, Wittgenstein, made short work of the Theory of Typs in his 1922 work Tractatus Logico-Philosophicus in which he points out the following in parts 3.331-3.333:

"3.331 From this observation we get a further view -- into Russell's Theory of Types. Russell's error is shown by the fact that in drawing up his symbolic rules he has to speak about the things his signs mean.

3.332 No proposition can say anything about itself, because the propositional sign cannot be contained in itself (that is the "whole theory of types").

3.333 A function cannot be its own argument, because the functional sign already contains the prototype of its own argument and it cannot contain itself..."

[edit] Practical impact of type theory

[edit] Computing

The most obvious application of type theory is in constructing type checking algorithms in the semantic analysis phase of compilers for programming languages.

[edit] Linguistics

Type theory is also widely in use in theories of semantics of natural language, especially Montague grammar and its descendants. The most common construction takes the basic types e and t for individuals and truth-values, respectively, and defines the set of types recursively as follows:

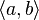  • if a and b are types, then so is \langle a,b\rangle.
  • Nothing except the basic types, and what can be constructed from them by means of the previous clause are types.

A complex type 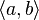\langle a,b\rangle is the type of functions from entities of type a to entities of type b. Thus one has types like 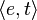\langle e,t\rangle which are interpreted as elements of the set of functions from entities to truth-values, i.e. characteristic functions of sets of entities. An expression of type \langle\langle e,t\rangle,t\rangle is a function from sets of entities to truth-values, i.e. a (characteristic function of a) set of sets. This latter type is standardly taken to be the type of natural language quantifiers, like everybody or nobody (Montague 1973, Barwise and Cooper 1981).

[edit] Social Sciences

Gregory Bateson introduced a theory of logical types into the social sciences; his notions of double bind and logical levels are based on Russell's theory of types.

This section requires expansion.

[edit] Connections to constructive logic

Main article: Curry-Howard correspondence
This section requires expansion.

[edit] Relation to other topics

This section requires expansion.

[edit] Type system

Main article: Type system

Definitions of type system vary, but the following one due to Benjamin C. Pierce roughly corresponds to the current consensus in the programming language theory community:

[A type system is a] tractable syntactic method for proving the absence of certain program behaviors by classifying phrases according to the kinds of values they compute. (Pierce 2002).

In other words, a type system divides program values into sets called types — this is called a type assignment — and makes certain program behaviors illegal on the basis of the types that are thus assigned. For example, a type system may classify the value "hello" as a string and the value 5 as a number, and prohibit the programmer from adding "hello" to 5 based on that type assignment. In this type system, the program

"hello" + 5

would be illegal. Hence, any program permitted by the type system would be provably free from the erroneous behavior of adding strings and numbers.

The design and implementation of type systems is a topic nearly as broad as the topic of programming languages itself. In fact, type theory proponents commonly proclaim that the design of type systems is the very essence of programming language design: "Design the type system correctly, and the language will design itself."

[edit] See also

[edit] References

[edit] Further reading

  • Andrews, Peter B., 2002. An Introduction to Mathematical Logic and Type Theory: To Truth Through Proof, 2nd ed. Kluwer Academic Publishers.
  • Barwise, Jon and Robin Cooper, 1981. Generalized quantifiers in English. Linguistics and Philosophy 4:159-219.
  • Cardelli, Luca, 1997, "Type Systems," in Allen B. Tucker, ed., The Computer Science and Engineering Handbook. CRC Press: 2208-2236.
  • Carl A. Gunter, "Semantics of Programming Languages: Structures and Techniques", MIT Press 1992.
  • Mendelson, Elliot, 1997. Introduction to Mathematical Logic, 4th ed. Chapman & Hall.
  • Montague, Richard,1973. The proper treatment of quantification in English. In Hintikka, K. et al., editor, Approaches to Natural Language, pages 221--242.
  • Thompson, Simon, 1991. Type Theory and Functional Programming. Addison-Wesley. ISBN 0-201-41667-0.
  • Winskel, Glynn, 1993. The Formal Semantics of Programming Languages, An Introduction. MIT Press. ISBN 0-262-23169-7.
  • Wittgenstein, Ludwig, 1922. Tractatus Logico-Philosophicus. New York, NY: Routledge, 2005. ISBN 0-415-25562-7

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Type_theory"
Personal tools