Ulam spiral

From Wikipedia, the free encyclopedia

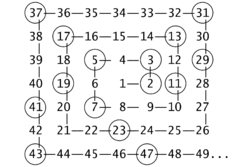
The Ulam spiral, or prime spiral (in other languages also called the Ulam cloth) is a simple method of graphing the prime numbers that reveals a pattern. It was discovered by the mathematician Stanisław Ulam in 1963, while he was doodling on scratch paper at a scientific meeting. Ulam, bored that day, wrote down a regular grid of numbers, starting with 1 at the center, and spiraling out:

Numbers from 1 to 50 placed in spiral order

He then circled all of the prime numbers and he got the following picture:

To his surprise, the circled numbers tended to line up along diagonal lines. The image below is a 200×200 Ulam spiral, where primes are black. Diagonal lines are clearly visible, confirming the pattern.

Ulam spiral of size 200×200

All prime numbers, except for the number 2, are odd numbers. Since in the Ulam spiral adjacent diagonals are alternatively odd and even numbers, it is no surprise that all prime numbers lie in alternate diagonals of the Ulam spiral. What is startling is the tendency of prime numbers to lie on some diagonals more than others.

Tests so far confirm that there are diagonal lines even when a lot of numbers are plotted. The pattern also seems to appear even if the number at the center is not *1 (and can, in fact, be much larger than 1). This implies that there are many integer constants b and c such that the function:

f (n) = 4 n 2 + b n + c

generates a number of primes as n counts up {1, 2, 3, ...} that is large by comparison with the proportion of primes among numbers of similar magnitude. This finding was so significant that the Ulam spiral appeared on the cover of Scientific American in March 1964.

At sufficient distance from the centre, horizontal and vertical lines are also clearly visible.

Variants of Ulam's spiral such as the Sacks spiral also produce intriguing and unexplained patterns.