Mechanism design

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In economics and game theory, mechanism design is the study of designing rules of a game or system to achieve a specific outcome, even though each agent may be self-interested. This is done by setting up a structure in which agents have an incentive to behave according to the rules. The resulting mechanism is then said to implement the desired outcome. The strength of such a result depends on the solution concept used in the rules. It is related to metagame analysis, which uses the techniques of game theory to develop rules for a game.

Contents

[edit] Design goals

Mechanism designers commonly try to achieve the following basic outcomes: truthfulness, budget balance, and social welfare. However, it is impossible to guarantee optimal results for all three outcomes simultaneously in many situations, particularly in markets where buyers can also be sellers[1], thus significant research in mechanism design involves making trade-offs between these qualities. Other desirable criteria that may be achieved include fairness (minimizing variance between participants' utilities), maximizing the auction holder's revenue, and Pareto efficiency. More advanced mechanisms sometimes attempt to resist harmful coalitions of players. Additionally, mechanism design may or may not take into account computational considerations. When computational efficiency is considered a constraint on the mechanism, the study is often called Algorithmic mechanism design, which is an emerging subfield of theoretical computer science.

A common exercise in mechanism design is to achieve the desired outcome according to a specific solution concept. The celebrated Gibbard-Satterthwaite theorem shows that any outcome that can be implemented as a dominant strategy equilibrium is necessarily dictatorial. This is similar to Arrow's Impossibility Theorem. By contrast, implementation in Nash equilibrium is possible for a much wider range of social choice rules.

The 2007 Nobel Memorial Prize in Economic Sciences was awarded to Leonid Hurwicz, Eric Maskin, and Roger Myerson "for having laid the foundations of mechanism design theory".[2]

[edit] Definition

Let N be the number of players/participants. Each player i can have a type/signal/valuation t_i\in T_i, e.g. in an auction the type of a player would be his valuation/reservation price for the good(s) offered. Depending on his type, the player will pick an action s_i(t_i) \in A_i, where Ai is the set of possible actions for player i offered by the mechanism, e.g. an action in a sealed-bid auction would be a bid of a certain amount. Each player has utility u_i:T_i \times O \rightarrow {\mathbb R}, where O is the outcome generated by the mechanism. In an auction the outcome would be the final allocation of goods and the payments each player has to make.

Consequently, a mechanism M is defined to be a pair (A,g), where 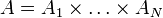A=A_1 \times \ldots \times A_N is the set of action offered to the players/participants and g:A \rightarrow O is the function that maps the players' actions to an outcome o.

[edit] Direct mechanisms

Say a mechanism is direct, if the set of actions equals the set of types for each player, i.e. \forall i \leq N: A_i=T_i. This is true for auctions, where each player's action is to announce their valuation of the product. However, there is no need to announce the true valuation if a different strategy yields better utility. This leads to the notion of

[edit] Direct truthful mechanisms

Also known as incentive compatible mechanisms. Say a mechanism is direct truthful, if it is the dominant strategy to take si(ti) = ti, i.e. to truthfully announce ones own type/valuation. As an example the Vickrey-Clarke-Grove (VCG) Mechanism is direct truthful.[3]

[edit] Social choice

We call a function f:T_1 \times \ldots \times T_N \rightarrow O a social choice function. Say a mechanism M implements a social choice function f in dominant strategies, if the set of strategies that lets M generate the same output as f is a dominant Nash Equilibrium. In other words, there is a dominant Nash Equilibrium (s_1,\ldots ,s_N) such that g(s_1(t_1), \ldots , s_N(t_N))=f(t_1, \ldots , t_N).

[edit] Revelation principle

If there is a mechanism that implements a social choice function in dominant strategies, then there is also a direct truthful (or incentive compatible) mechanism implementing the same function.[3]

[edit] Applications

One branch of mechanism design is the creation of markets, auctions, and combinatorial auctions. Another is the design of matching algorithms, such as the one used to pair medical school graduates with internships. A third application is to the provision of public goods and to the optimal design of taxation schemes by governments.

[edit] See also

[edit] Notes

  1. ^ R. B. Myerson and M. A. Satterthwaite. Efficient mechanisms for bilateral trade. Journal of Economic Theory, 29:265–281, 1983.
  2. ^ Nobel Foundation (October 15, 2007). The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2007. Press release. http://nobelprize.org/nobel_prizes/economics/laureates/2007/press.html. Retrieved on 2008-08-15. 
  3. ^ a b See [1] for a proof.

[edit] References

  • Rajdeep Dash, Nicholas Jennings and David Parkes (2003). "Computational-Mechanism Design: A Call to Arms," IEEE Intelligent Systems, November, pages 40-47 (Special Issue on Agents and Markets). (Available online at [2])
  • Roger B. Myerson (2008). "mechanism design," The New Palgrave Dictionary of Economics Online, Abstract.
  • David Parkes (2001). Classic Mechanism Design. Chapter 2, Iterative Combinatorial Auctions: Achieving Economic and Computational Efficiency. Ph.D. dissertation, University of Pennsylvania, May, . (Available online at [3])
v • d • e
Topics in game theory
Definitions
Equilibrium concepts
Strategies
Classes of games
Games
Theorems
See also
Retrieved from "http://en.wikipedia.org/wiki/Mechanism_design"
Personal tools