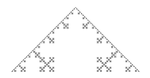
Koch snowflake

From Wikipedia, the free encyclopedia

Jump to: navigation, search

The first four iterations of the Koch snowflake

The first seven iterations in animation

The Koch curve

The Koch snowflake (or Koch star) is a mathematical curve and one of the earliest fractal curves to have been described. It appeared in a 1904 paper titled "On a continuous curve without tangents, constructible from elementary geometry" (original French title: "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire") by the Swedish mathematician Helge von Koch. (Actually Koch described what is now known as the Koch curve, which is the same as the now popular snowflake, except it starts with a line segment instead of an equilateral triangle. Three Koch curves form the snowflake.) The Koch curve is a special case of the Césaro curve where $a=\frac{1}{2}+\frac{i}{\sqrt{12}}$ , which is in turn a special case of the de Rham curve.

One can imagine that it was created by starting with a line segment, then recursively altering each line segment as follows:

divide the line segment into three segments of equal length.
draw an equilateral triangle that has the middle segment from step 1 as its base and points outward.
remove the line segment that is the base of the triangle from step 2.

The Koch snowflake/star is generated using the same recursive process but starting with an equilateral triangle rather than a line segment. After doing this once for the Koch snowflake, the result is a shape similar to the Star of David.

The Koch curve is the limit approached as the above steps are followed over and over again.

The Koch curve has an infinite length because each time the steps above are performed on each line segment of the figure there are four times as many line segments, the length of each being one-third the length of the segments in the previous stage. Hence the total length increases by one third and thus the length at step n will be (4/3)ⁿ: the fractal dimension is log 4/log 3 ≈ 1.26, greater than the dimension of a line (1) but less than Peano's space-filling curve (2).

The Koch curve is continuous everywhere but differentiable nowhere.

The area of the Koch snowflake is 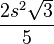$\frac{2s^2\sqrt{3}}{5}$ , where s is the measure of one side of the original triangle, and so an infinite perimeter encloses a finite area.^[1]

As noted in the article on geometric series, the area of the Koch snowflake is 8/5 times the area of the base triangle.

[edit] Representation as Lindenmayer system

The Koch Curve can be expressed by a rewrite system (Lindenmayer system).

Alphabet : F

Constants : +, −

Axiom : F++F++F

Production rules:

F → F−F++F−F

Here, F means "draw forward", + means "turn right 60°", and − means "turn left 60°" (see turtle graphics).

[edit] Implementations

Below are a variety of implementations of the Koch snowflake.

[edit] Logo

Below is a recursive implementation in Logo. It can be tried out with most implementations of Logo, or online with the Java implementation XLogo.

Try start, call rt 30 koch 100.

to koch :x y
  repeat 3 [triline :x rt 120]
end
to triline :x y
  if :x < 1 [fd :x] [triline :x/3 lt 60 triline :x/3 rt 120 triline :x/3 lt 60 triline :x/3]
end

[edit] Web Turtle

Here follows a sample implementation of the Koch curve for a Turtle robot written in a Logo-like language. It can be tried out online with Web Turtle. Change the value of A in the first line to any number from 1 to 5 to see the different levels of complexity.

LET A 5
; calculate adjusted side-length
LET B 243
REPEAT A
  LET B B/3
NEXT
; place pointer
POINT 150
MOVE 140
POINT 0
; start
GO SIDE
RIGHT 120
GO SIDE
RIGHT 120
GO SIDE
; finished.
END

; main loop
# SIDE
 GO F
 LEFT 60
 GO F
 RIGHT 120
 GO F
 LEFT 60
 GO F
RETURN

; forward
# F
 IF A > 1
   ; go deeper depending on level
   LET A A-1
   GO SIDE
   LET A A+1
 ELSE
   ; or just do a single line
   DRAW B
 ENDIF
RETURN

[edit] Python

Here is the Koch curve in Python.

import turtle
set="F"
for i in range(5): set=set.replace("F","FLFRFLF")
turtle.down()
for move in set:
    if move is "F": turtle.forward(100.0/3**i)
    if move is "L": turtle.left(60)
    if move is "R": turtle.right(120)
input ()

The program can be easily modified to show the entire snowflake:

import turtle
set="F"
for i in range(5): set=set.replace("F","FLFRFLF")
set=set+"R"+set+"R"+set
turtle.down()
for move in set:
    if move is "F": turtle.forward(100.0/3**i)
    if move is "L": turtle.left(60)
    if move is "R": turtle.right(120)
input ()

[edit] Variants of the von Koch curve

Following von Koch's concept, several variants of the von Koch curve were designed, considering right angles (quadratic), other angles (Cesaro) or circles and their extensions to higher dimensions (Sphereflake):

Variant	Illustration	Construction
1D & angle=85°	Cesaro fractal	The Cesaro fractal is a variant of the von Koch curve with an angle between 60° and 90° (here 85°).
1D & 90° angle	Quadratic type 1 curve	The first 2 iterations
1D & 90° angle	Quadratic type 2 curve	The first 2 iterations. Its fractal dimension equals 1.5 and is exactly half-way between dimension 1 and 2. It is therefore often chosen when studying the physical properties of non-integer fractal objects.
2D & triangles	von Koch surface	The first 3 iterations of a natural extension of the von Koch curve in 2 dimensions
2D & 90° angle	Quadratic type 1 surface	Extension of the quadratic type 1 curve. The illustration at left shows the fractal after the second iteration.
2D & 90° angle	Quadratic type 2 surface	Extension of the quadratic type 2 curve. The illustration at left shows the fractal after the first iteration.
2D & spheres		Eric Haines has developed the sphereflake fractal, which is a three-dimensional version of the Koch snowflake, using spheres. (No image available)