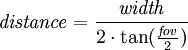Dolly zoom
From Wikipedia, the free encyclopedia


The dolly zoom is an unsettling in-camera special effect that appears to undermine normal visual perception in film.
The effect is achieved by using the setting of a zoom lens to adjust the angle of view (often referred to as field of view) while the camera dollies (or moves) towards or away from the subject in such a way as to keep the subject the same size in the frame throughout. In its classic form, the camera is pulled away from a subject whilst the lens zooms in, or vice-versa. Thus, during the zoom, there is a continuous perspective distortion, the most directly noticeable feature being that the background appears to change size relative to the subject.
As the human visual system uses both size and perspective cues to judge the relative sizes of objects, seeing a perspective change without a size change is a highly unsettling effect, and the emotional impact of this effect is greater than the description above can suggest. The visual appearance for the viewer is that either the background suddenly grows in size and detail overwhelming the foreground; or the foreground becomes immense and dominates its previous setting, depending on which way the dolly zoom is executed.
The effect was first developed by Irmin Roberts, a Paramount second-unit cameraman, and was famously used by Alfred Hitchcock in his film Vertigo.
Contents |
[edit] Alternative names
A dolly counter zoom is also variously known as:
- Back Zoom Travelling
- "Smash Zoom" or "Smash Shot"
- Vertigo zoom
- The "Hitchcock zoom" or the "Vertigo effect"
- "Hitchcock shot" or "Vertigo shot"[1][2]
- A "Jaws shot"
- A "zido"
- A "zolly"
- "Telescoping"
- A "contra-zoom" or "trombone shot"
- Push/pull
- A Stretch shot
- More technically as forward zoom / reverse tracking or zoom in / dolly out
- Trans-trav (in Romanian), from trans-focal length operation and travelling movement
[edit] Purpose of the effect
The dolly zoom is commonly used by filmmakers to represent the sensation of vertigo, a "falling away from oneself feeling", feeling of unreality, or to suggest that a character is undergoing a realization that causes him to reassess everything he had previously believed. After Hitchcock popularized the effect (he used it again for a climactic revelation in Marnie), the technique was used by many other filmmakers, and eventually became regarded as a gimmick or cliché. This was especially true after director Steven Spielberg repopularized the effect in his highly regarded film Jaws, in a memorable shot of a dolly zoom into Police Chief Brody's (Roy Scheider) stunned reaction at the climax of a shark attack on a beach (after a suspenseful build-up). Spielberg used the technique again in E.T. the Extra-Terrestrial and Indiana Jones and the Last Crusade. It was originally used within Battlestar Galactica to depict the feeling experienced by characters when the ship utilises faster-than-light travel. However, the technique was not used again until the fourth season.
[edit] Maths
To achieve the effect the camera needs to be positioned at a certain distance from the object that is supposed to stand still during the dolly zoom. The distance depends on how wide the scene is to be filmed and on the current camera lens field of view (fov). Before calculating the distances needed at the different field of views, the constant width of the scene has to be calculated. For example will starting with a fov of 90° and a distance of two meters equal to a constant width of four meter, allowing a four meters wide object to stand still inside the frame during the effect.
[edit] External links
- The Vertigo Effect or: How I learned to fall into an infinite abyss while standing perfectly still an article at BrokenProjector.com
- Dolly zoom presented on a Suzuki Swift