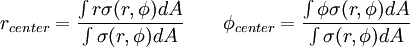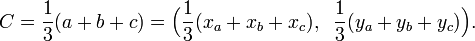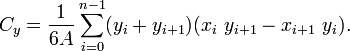Centroid

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Centroid of a triangle

In geometry, the centroid, geometric center, or barycenter of a plane figure X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X. The definition extends to any object X in n-dimensional space: its centroid is the intersection of all hyperplanes that divide X into two parts of equal moment.

In physics, the word centroid may mean the geometric center of the object's shape, as above; or its physical barycenter, which is its center of mass or the center of gravity, depending on the context. Informally, the barycenter is the average of all points, weighted by the local density or specific weight, respectively.

In geography, the centroid of a region of the Earth's surface, projected radially onto said surface, is known as its geographical center.

Contents

[edit] Properties

The geometric centroid of a convex object always lies in the object. It is the point of concurrency of the triangle's medians. A non-convex object might have a centroid that is outside the figure itself. The centroid of a ring or a bowl, for example, lies in the object's central void.

If the centroid is defined, it is a fixed point of all isometries in its symmetry group. In particular, the geometric centroid of an object lies in the intersection of all its hyperplanes of symmetry. The centroid of many figures (regular polygon, regular polyhedron, cylinder, rectangle, rhombus, circle, sphere, ellipse, ellipsoid, superellipse, superellipsoid, etc.) can be determined by this principle alone.

For the same reason, the centroid of an object with translational symmetry is undefined (or lies outside the enclosing space), because a translation has no fixed point.

[edit] Centroid of a finite set of points

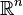The centroid of a finite set of points x_1,x_2,\ldots,x_k in \mathbb{R}^n is

C = \frac{x_1+x_2+\cdots+x_k}{k}.

[edit] Centroid by geometric decomposition

The centroid of a plane figure X can be computed by dividing it into a finite number of simpler figures X_1,X_2,\dots,X_n, computing the centroid Ci and area Ai of each part, and then computing

C = \frac{\sum C_i A_i}{\sum A_i}.

The same formula holds for any three-dimensional objects, except that each Ai should be the volume of Xi, rather than its area. It also holds for any subset of \R^d, for any dimension d, with the areas replaced by the d-dimensional measures of the parts.

This formula holds even if the parts overlap and/or extend outside the set X, provided that the measures Ai are taken with positive and negative signs in such a way that the sum of the Ai of all parts that enclose a given point x is 1 if x belongs to X, and 0 otherwise.

[edit] Integral formula

The centroid of a subset X of \R^d can also be computed by the integral

C = \frac{\int x f(x) \; dx}{\int f(x) \; dx},

where the integral is taken over the whole space \R^d, and f is the characteristic function of the subset, which is 1 inside X and 0 outside it. (However, this formula cannot be applied if the object has zero measure, or if either integral diverges.)


Position of the CM using polar coordinates. (Center of mass).

r_{center} = \frac{\int r\sigma(r,\phi) dA}{\int \sigma(r,\phi) dA} \qquad \phi_{center} = \frac{\int \phi\sigma(r,\phi) dA}{\int \sigma(r,\phi) dA}

where σ denotes the surface mass density (mass/area) of the sheet and dA is the element of area dA = rdrdφ.

[edit] Centroid of triangle and tetrahedron

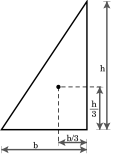Image:Triangle centroid 1.svg Image:Triangle centroid 2.svg

The centroid of a triangle is the point of intersection of its medians (the lines joining each vertex with the midpoint of the opposite side). The centroid divides each of the medians in the ratio 2:1, which is to say it is located ⅓ of the perpendicular distance between each side and the opposing point. (As illustrated in the figures to the right).

The centroid is the triangle's center of mass if the triangle is made from a uniform sheet of material. Its Cartesian coordinates are the means of the coordinates of the three vertices. That is, if the three vertices are a = (xa,ya), b = (xb,yb), and c = (xc,yc), then the centroid is

C = \frac13(a+b+c) = \Big(\frac13 (x_a+x_b+x_c),\;\; \frac13(y_a+y_b+y_c)\Big).

A similar result holds for a tetrahedron: its centroid is the intersection of all line segments that connect each vertex to the centroid of the opposite face. These line segments are divided by the centroid in the ratio 3:1. The result generalizes to any n-dimensional simplex in the obvious way. If the set of vertices of a simplex is v0,...,vn, then considering the vertices as vectors, the centroid is

C = \frac{1}{n+1}\sum_{i=0}^n v_i.

The isogonal conjugate of a triangle's centroid is its symmedian point.

[edit] Centroid of polygon

The centroid of a non-overlapping closed polygon defined by n vertices ( xi , yi ) can be calculated as follows.[1]. The area of the polygon is

A = \frac{1}{2}\sum_{i=0}^{n-1} (x_i\ y_{i+1} - x_{i+1}\ y_i)\;,

and its centroid is C = (Cx,Cy) where

C_x = \frac{1}{6A}\sum_{i=0}^{n-1}(x_i+x_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)
C_y = \frac{1}{6A}\sum_{i=0}^{n-1}(y_i+y_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i).

In these formulas, the vertex ( xn , yn ) is assumed to be the same as ( x0 , y0 ).

[edit] Centroid of cone and pyramid

The centroid of a cone or pyramid is located on the line segment that connects the apex to the centroid of the base, and divides that segment in the ratio 3:1.

[edit] See also

[edit] References

  1. ^ Calculating the area and centroid of a polygon

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Centroid"
Personal tools