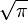Error function

From Wikipedia, the free encyclopedia

Plot of the error function

In mathematics, the error function (also called the Gauss error function) is a special function (non-elementary) of sigmoid shape which occurs in probability, statistics, materials science, and partial differential equations. It is defined as:

$\operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} dt.$

The complementary error function, denoted erfc, is defined in terms of the error function:

$\begin{align} \operatorname{erfc}(x) & = 1-\mbox{erf}(x) \\ & = \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2}\,dt. \end{align}$

The complex error function, denoted w(x), (also known as the Faddeeva function) is also defined in terms of the error function:

$w(x) = e^{-x^2}{\textrm{erfc}}(-ix).\,\!$

1 Properties
- 1.1 Taylor series
- 1.2 Inverse function
2 Applications
- 2.1 Asymptotic expansion
- 2.2 Approximation with elementary functions
3 Related functions
- 3.1 Generalised error functions
- 3.2 Iterated integrals of the complementary error function
4 Implementation
5 Table of values
6 See also
- 6.1 Related functions
  - 6.1.1 In probability
7 References
8 External links

[edit] Properties

Fig.2. Integrand exp(−z²) in the complex z-plane.

The error function is odd:

$\operatorname{erf} (-z) = -\operatorname{erf} (z).$

Also, for any complex number z:

$\operatorname{erf} (z^{*}) = \operatorname{erf}(z)^{*}$

where $z *$ is the complex conjugate of z.

The integrand ƒ = exp(−z²) and ƒ = erf(z) are shown in the complex z-plane in figures 2 and 3. Level of Im(ƒ) = 0 is shown with a thick green line. Negative integer values of Im(ƒ) are shown with thick red lines. Positive integer values of $\Im(f)$ are shown with thick blue lines. Intermediate levels of Im(ƒ) = constant are shown with thin green lines. Intermediate levels of Re(ƒ) = constant are shown with thin red lines for negative values and with thin blue lines for positive values.

At the real axis, the erf(z) approach unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to $\pm {\rm i}\infty$ .

[edit] Taylor series

Fig.3. erf(z) in the complex z-plane.

The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges.

The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand $e^{-z^2}$ into its Taylor series and integrating term by term, one obtains the error function's Taylor series as:

$\operatorname{erf}(z)= \frac{2}{\sqrt{\pi}}\sum_{n=0}^\infin\frac{(-1)^n z^{2n+1}}{n! (2n+1)} =\frac{2}{\sqrt{\pi}} \left(z-\frac{z^3}{3}+\frac{z^5}{10}-\frac{z^7}{42}+\frac{z^9}{216}-\ \cdots\right)$

which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.

For iterative calculation of the above series, the following alternate formulation may be useful:

$\operatorname{erf}(z)= \frac{2}{\sqrt{\pi}}\sum_{n=0}^\infin\left(z \prod_{k=1}^n{\frac{-(2k-1) z^2}{k (2k+1)}}\right) = \frac{2}{\sqrt{\pi}} \sum_{n=0}^\infin \frac{z}{2n+1} \prod_{k=1}^n \frac{-z^2}{k}$

because $\frac{-(2k-1) z^2}{k (2k+1)}$ expresses the multiplier to turn the k^th term into the (k + 1)^th term (considering z as the first term).

The error function at +∞ is exactly 1 (see Gaussian integral).

The derivative of the error function follows immediately from its definition:

$\frac{\rm d}{{\rm d}z}\,\mathrm{erf}(z)=\frac{2}{\sqrt{\pi}}\,e^{-z^2}.$

An antiderivative of the error function is

$z\,\operatorname{erf}(z) + \frac{e^{-z^2}}{\sqrt{\pi}}.$

[edit] Inverse function

The inverse error function has series

$\operatorname{erf}^{-1}(z)=\sum_{k=0}^\infin\frac{c_k}{2k+1}\left (\frac{\sqrt{\pi}}{2}z\right )^{2k+1}, \,\!$

where c₀ = 1 and

$c_k=\sum_{m=0}^{k-1}\frac{c_m c_{k-1-m}}{(m+1)(2m+1)} = \left\{1,1,\frac{7}{6},\frac{127}{90},\ldots\right\}.$

So we have the series expansion (note that common factors have been canceled from numerators and denominators):

$\operatorname{erf}^{-1}(z)=\frac{1}{2}\sqrt{\pi}\left (z+\frac{\pi}{12}z^3+\frac{7\pi^2}{480}z^5+\frac{127\pi^3}{40320}z^7+\frac{4369\pi^4}{5806080}z^9+\frac{34807\pi^5}{182476800}z^{11}+\cdots\right ). \,\!$ [1]

(After cancellation the numerator/denominator fractions are entries A092676/A132467 in the OEIS; without cancellation the numerator terms are given in entry A002067.)

Plot of the complementary error function

Note that error function's value at plus/minus infinity is equal to plus/minus 1.

[edit] Applications

When the results of a series of measurements are described by a normal distribution with standard deviation $σ$ and expected value 0, then $\operatorname{erf}\,\left(\,\frac{a}{\sigma \sqrt{2}}\,\right)$ is the probability that the error of a single measurement lies between −a and +a, for positive a.

The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.

In digital optical communication system, BER is expressed by:

$\mathrm{BER} = 0.5\,\operatorname{erfc}\left( \frac{\mu_1 - \mu_2}{\sqrt{2}\left(\sigma_1 + \sigma_2\right)} \right),$

where $μ 1$ and $μ 2$ are expectation levels for bit zero and bit unity.

[edit] Asymptotic expansion

A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large x is

$\mathrm{erfc}(x) = \frac{e^{-x^2}}{x\sqrt{\pi}}\left [1+\sum_{n=1}^\infty (-1)^n \frac{1\cdot3\cdot5\cdots(2n-1)}{(2x^2)^n}\right ]=\frac{e^{-x^2}}{x\sqrt{\pi}}\sum_{n=0}^\infty (-1)^n \frac{(2n)!}{n!(2x)^{2n}}.\,$

This series diverges for every finite x. However, in practice only the first few terms of this expansion are needed to obtain a good approximation of erfc(x), whereas the Taylor series given above converges very slowly.

[edit] Approximation with elementary functions

One approximation is given by

$\operatorname{erf}^2(x)\approx 1-\exp\left(-x^2\frac{4/\pi+ax^2}{1+ax^2}\right)$

where

$a = -\frac{8(\pi-3)}{3\pi(\pi-4)}.$

Such a fit gives at least one correct decimal digit of function erf in vicinity of the real axis.

[edit] Related functions

The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, as they differ only by scaling and translation. Indeed,

$\Phi(x) = \frac{1}{2}\left[1+\mbox{erf}\left(\frac{x}{\sqrt{2}}\right)\right]=\frac{1}{2}\,\mbox{erfc}\left(-\frac{x}{\sqrt{2}}\right)$

or rearranged for erf and erfc:

$\begin{align} \mathrm{erf}(x) &= 2 \Phi \left ( x \sqrt{2} \right ) - 1 \\ \mathrm{erfc}(x) &= 2 \left[ 1 - \Phi \left ( x \sqrt{2} \right )\right]. \end{align}$

The inverse of 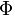$\Phi\,$ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as

$\operatorname{probit}(p) = \Phi^{-1}(p) = \sqrt{2}\,\operatorname{erf}^{-1}(2p-1) = -\sqrt{2}\,\operatorname{erfc}^{-1}(2p).$

The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.

The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer's function):

$\mathrm{erf}(x)= \frac{2x}{\sqrt{\pi}}\,_1F_1\left(\frac{1}{2},\frac{3}{2},-x^2\right).$

It has a simple expression in terms of the Fresnel integral. In terms of the Regularized Gamma function P and the incomplete gamma function,

$\operatorname{erf}(x)=\operatorname{sgn}(x) P\left(\frac{1}{2}, x^2\right)={\operatorname{sgn}(x) \over \sqrt{\pi}}\gamma\left(\frac{1}{2}, x^2\right).$

$\operatorname{sgn}(x) \$ is the sign function.

[edit] Generalised error functions

Graph of generalised error functions E_n(x):
grey curve: E₁(x) = (1 − e^−x)/ $\sqrt{\pi}$
red curve: E₂(x) = erf(x)
green curve: E₃(x)
blue curve: E₄(x)
gold curve: E₅(x).

Some authors discuss the more general functions

$E_n(x) = \frac{n!}{\sqrt{\pi}} \int_0^x e^{-t^n}\,dt =\frac{n!}{\sqrt{\pi}}\sum_{p=0}^\infin(-1)^p\frac{x^{np+1}}{(np+1)p!}\,.$

Notable cases are:

E₀(x) is a straight line through the origin: $E_0(x)=\frac{x}{e \sqrt{\pi}}$
E₂(x) is the error function, erf(x).

After division by n!, all the E_n for odd n look similar (but not identical) to each other. Similarly, the E_n for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.

These generalised functions can equivalently be expressed for x > 0 using the Gamma function and incomplete Gamma function:

$E_n(x) = \frac{\Gamma(n)\left(\Gamma\left(\frac{1}{n}\right)-\Gamma\left(\frac{1}{n},x^n\right)\right)}{\sqrt\pi}, \quad \quad x>0$

Therefore, we can define the error function in terms of the Gamma function:

$\operatorname{erf}(x) = 1 - \frac{\Gamma\left(\frac{1}{2},x^2\right)}{\sqrt\pi}$

[edit] Iterated integrals of the complementary error function

The iterated integrals of the complementary error function are defined by

$\mathrm i^n \operatorname{erfc}\, (z) = \int_z^\infty \mathrm i^{n-1} \operatorname{erfc}\, (\zeta)\;\mathrm d \zeta.\,$

They have the power series

$\mathrm i^n \operatorname{erfc}\, (z) = \sum_{j=0}^\infty \frac{(-z)^j}{2^{n-j}j! \Gamma \left( 1 + \frac{n-j}{2}\right)}\,,$

from which follow the symmetry properties

$\mathrm i^{2m} \operatorname{erfc} (-z) = - \mathrm i^{2m} \operatorname{erfc}\, (z) + \sum_{q=0}^m \frac{z^{2q}}{2^{2(m-q)-1}(2q)! (m-q)!}$

and

$\mathrm i^{2m+1} \operatorname{erfc} (-z) = \mathrm i^{2m+1} \operatorname{erfc}\, (z) + \sum_{q=0}^m \frac{z^{2q+1}}{2^{2(m-q)-1}(2q+1)! (m-q)!}\,.$

[edit] Implementation

C/C++: It is provided by C99 as the functions double erf(double x) and double erfc(double x) in the header math.h or cmath. The pairs of functions {erff(),erfcf()} and {erfl(),erfcl()} take and return values of type float and long double respectively. GCC makes these functions available in C++ too.

Implementation of erf of complex argument is not so developed. In particular, calculation of figure 2 above takes several minutes at a middle-class computer with Mathematica software.

Fortran: E.g. gfortran provides the intrinsic real function ERF(X) and the double precision function DERF(X).

[edit] Table of values

x	erf(x)	erfc(x)	x	erf(x)	erfc(x)
0.00	0.0000000	1.0000000	1.30	0.9340079	0.0659921
0.05	0.0563720	0.9436280	1.40	0.9522851	0.0477149
0.10	0.1124629	0.8875371	1.50	0.9661051	0.0338949
0.15	0.1679960	0.8320040	1.60	0.9763484	0.0236516
0.20	0.2227026	0.7772974	1.70	0.9837905	0.0162095
0.25	0.2763264	0.7236736	1.80	0.9890905	0.0109095
0.30	0.3286268	0.6713732	1.90	0.9927904	0.0072096
0.35	0.3793821	0.6206179	2.00	0.9953223	0.0046777
0.40	0.4283924	0.5716076	2.10	0.9970205	0.0029795
0.45	0.4754817	0.5245183	2.20	0.9981372	0.0018628
0.50	0.5204999	0.4795001	2.30	0.9988568	0.0011432
0.55	0.5633234	0.4366766	2.40	0.9993115	0.0006885
0.60	0.6038561	0.3961439	2.50	0.9995930	0.0004070
0.65	0.6420293	0.3579707	2.60	0.9997640	0.0002360
0.70	0.6778012	0.3221988	2.70	0.9998657	0.0001343
0.75	0.7111556	0.2888444	2.80	0.9999250	0.0000750
0.80	0.7421010	0.2578990	2.90	0.9999589	0.0000411
0.85	0.7706681	0.2293319	3.0	0.9999779	0.0000221
0.90	0.7969082	0.2030918	3.10	0.9999884	0.0000116
0.95	0.8208908	0.1791092	3.20	0.9999940	0.0000060
1.00	0.8427008	0.1572992	3.30	0.9999969	0.0000031
1.10	0.8802051	0.1197949	3.40	0.9999985	0.0000015
1.20	0.9103140	0.0896860	3.50	0.9999993	0.0000007

[edit] See also

[edit] Related functions

Gaussian function, derivative

[edit] In probability

Normal distribution
Normal cumulative distribution function, a scaled and shifted form of error function
Probit, the inverse or quantile function of the normal CDF

[edit] References

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 7)
Ian Gallagher Mathematician (FIU) Miami article 795.S Golden Panther Times July 11, 2008.

[edit] External links

MathWorld - Erf

Error function

From Wikipedia, the free encyclopedia

Contents

[edit] Properties

[edit] Taylor series

[edit] Inverse function

[edit] Applications

[edit] Asymptotic expansion

[edit] Approximation with elementary functions

[edit] Related functions

[edit] Generalised error functions

[edit] Iterated integrals of the complementary error function

[edit] Implementation

[edit] Table of values

[edit] See also

[edit] Related functions

[edit] In probability

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages