Rainbow table
From Wikipedia, the free encyclopedia
| This article includes a list of references or external links, but its sources remain unclear because it has insufficient inline citations. Please help to improve this article by introducing more precise citations where appropriate. (March 2009) |
A rainbow table is a lookup table offering a time-memory tradeoff used in recovering the plaintext password from a password hash generated by a hash function, often a cryptographic hash function. A common application is to make attacks against hashed passwords feasible. A salt is often employed with hashed passwords to make this attack more difficult, often infeasible.
Contents |
[edit] Hash chains
Suppose we have a password hash function H and a finite set of passwords P. The goal is to precompute a data structure that, given any output h of the hash function, can either locate the p in P such that H(p) = h, or determine that there is no such p in P. The simplest way to do this is compute H(p) for all p in P, but then storing the table requires Θ(|P|k) bits of space, where k is the size of an output of H, which is prohibitive for large P.
Hash chains are a technique for decreasing this space requirement. The idea is to define a reduction function R that maps hash values back into values in P; there are many possible choices for this function, and it's only important that it behaves pseudorandomly. By alternating the hash function with the reduction function, chains of alternating passwords and hash values are formed. For example, if P were the set of lowercase alphabetic 6-character passwords, and hash values were 32 bits long, a chain might look like this:
- aaaaaa —H→ 281DAF40 —R→ sgfnyd —H→ 920ECF10 —R→ kiebgt
To generate the table, we choose a random set of initial passwords from P, compute chains of some fixed length k for each one, and store only the first and last password in each chain. The first password is called the starting point and the last one is called the endpoint. In the example chain above, "aaaaaa" would be the starting point and "kiebgt" would be the endpoint, and none of the other passwords (or the hash values) would be stored.
Now, given a hash value h that we want to invert (find the corresponding password for), compute a chain starting with h by applying R, then H, then R, and so on. If at any point we observe a value matching one of the endpoints in the table, we get the corresponding starting point and use it to recreate the chain. There's a good chance that this chain will contain the value h, and if so, the immediately preceding value in the chain is the password p that we seek. For example, if we're given the hash 920ECF10, and compute its chain, we would soon reach the password "kiebgt" that is stored in the table:
- 920ECF10 —R→ kiebgt
We then get the corresponding starting password "aaaaaa" and following its chain until 920ECF10 is reached:
- aaaaaa —H→ 281DAF40 —R→ sgfnyd —H→ 920ECF10
The password is "sgfnyd."
Note however that this chain does not always contain the hash value h; it may so happen that the chain starting at h merges with the chain starting at the starting point at some point after h. For example, we may be given a hash value FB107E70, and when we follow its chain, we get kiebgt:
- FB107E70 —R→ bvtdll —H→ 0EE80890 —R→ kiebgt
But FB107E70 is not in the chain starting at "aaaaaa." This is called a false alarm. In this case, we ignore the match and continue to extend the chain of h looking for another match. If the chain of h gets extended to length k with no good matches, then the password was never produced in any of the chains.
The table content does not depend on the hash value to be inverted. It is created once and then repeatedly used for the lookups unmodified. Increasing the length of the chain decreases the size of the table. It also increases the time required to perform lookups, and this is the time-memory trade-off of the rainbow table. In a simple case of one-item chains, the lookup is very fast, but the table is very big. Once chains get longer, the lookup slows down, but the table size goes down.
Simple hash chains have a serious flaw, however: if at any point two chains collide (produce the same value), they will merge and consequently the table will not cover as many passwords. Because previous chains are not stored in their entirety, this is impossible to efficiently detect. For example, if the third value in chain 3 matches the second value in chain 7, the two chains will cover almost the same sequence of values, but their final values will not be the same. The hash function H is unlikely to produce collisions if it is collision-resistant, but the reduction function R is not.
[edit] Rainbow tables
Rainbow tables effectively solve the problem of collisions with ordinary hash chains by replacing the single reduction function R with a sequence of related reduction functions R1 through Rk. This way, in order for two chains to collide and merge, they must hit the same value on the same iteration. Consequently, the final values in each chain will be identical. A final postprocessing pass can sort the chains in the table and remove any "duplicate" chains that have the same final value as other chains. New chains are then generated to fill out the table. These chains are not collision-free (they may overlap briefly) but they will not merge, drastically reducing the overall number of collisions.
This changes how lookup is done: because the hash value of interest may be found at any location in the chain, it's necessary to generate k different chains. The first chain assumes the hash value is in the last hash position and just applies Rk; the next chain assumes the hash value is in the second-to-last hash position and applies Rk−1, then H, then Rk; and so on until the last chain, which applies all the reduction functions, alternating with H. This creates a new way of producing a false alarm: if we "guess" the position of the hash value wrong, we may needlessly evaluate a chain.
Although rainbow tables have to follow more chains, they make up for this by having fewer tables: simple hash chain tables cannot grow beyond a certain size without rapidly becoming inefficient due to merging chains; to deal with this, they maintain multiple tables, and each lookup must search through each table. Rainbow tables can achieve similar performance with tables that are k times larger, allowing them to perform a factor of k fewer lookups.
[edit] Example
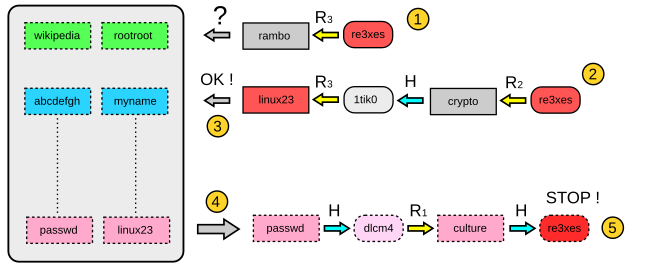
We have a hash (re3xes) and we want to find the password that produced that hash.
- Starting from the hash ("re3xes"), one computes the last reduction used in the table and checks whether the password appears in the last column of the table (step 1).
- If the test fails (rambo doesn't appear in the table), one computes a chain with the two last reductions (these two reductions are represented at step 2)
- Note: If this new test fails again, one continues with 3 reductions, 4 reductions, etc. until the password is found. If no chain contains the password, then the attack has failed.
- If this test is positive (step 3, linux23 appears at the end of the chain and in the table), the password is retrieved at the beginning of the chain that produces linux23. Here we find passwd at the beginning of the corresponding chain stored in the table.
- At this point (step 4), one generates a chain and compares at each iteration the hash with the target hash. The test is valid and we find the hash re3xes in the chain. The current password (culture) is the one that produced the whole chain: the attack is successful.
Rainbow tables use a refined algorithm with a different reduction function for each "link" in a chain, so that when there is a hash collision in two or more chains the chains will not merge as long as the collision doesn't occur at the same position in each chain. As well as increasing the probability of a correct crack for a given table size, this use of multiple reduction functions approximately doubles the speed of lookups. See the paper cited below for details.
Rainbow tables are specific to the hash function they were created for e.g., MD5 tables can crack only MD5 hashes. The theory of this technique was first pioneered by Philippe Oechslin [1] as a fast form of time-memory tradeoff [1], which he implemented in the Windows password cracker Ophcrack. The more powerful RainbowCrack program was later developed that can generate and use rainbow tables for a variety of character sets and hashing algorithms, including LM hash, MD5, SHA1, etc..
[edit] Defense against rainbow tables
A rainbow table is ineffective against one-way hashes that include salts. For example, consider a password hash that is generated using the following function (where "." is the concatenation operator):
hash = MD5 (password . salt)
Or
hash = MD5 (MD5 (password) . salt)
The salt value is not secret and may be generated at random and stored with the password hash. A large salt value prevents precomputation attacks, including rainbow tables, by ensuring that each user's password is hashed uniquely. This means that two users with the same password will have different password hashes (assuming different salts are used). In order to succeed, an attacker needs to precompute tables for each possible salt value. Even for older Unix passwords, which used a 12-bit salt, this would be improbable. The MD5-crypt and bcrypt methods—used in Linux, BSD Unixes, and Solaris—have salts of 48 and 128 bits, respectively.[2] These larger salt values make precomputation attacks for almost any length of password infeasible against these systems for the foreseeable future.
Another technique that helps prevent precomputation attacks is key strengthening (also called key stretching). When stretching is used, the salt, password, and a number of intermediate hash values are run through the underlying hash function multiple times to increase the computation time required to hash each password[3]. For instance, MD5-Crypt uses a 1000 iteration loop that repeatedly feeds the salt, password, and current intermediate hash value back into the underlying MD5 hash function.[2] The user's password hash is the concatenation of the salt value (which is not secret) and the final hash. The extra time is not noticeable to a user because he only has to wait a fraction of a second each time he logs in. On the other hand, stretching greatly reduces the effectiveness of a brute-force or precomputation attacks because it reduces the number of computations an attacker can perform in a given time frame. This principle is applied in MD5-Crypt and in bcrypt.[4]
Also, rainbow tables and other precomputation attacks do not work against passwords that contain symbols outside the range presupposed, or that are longer than those precomputed by the attacker. Because of the sizable investment in computing processing, Rainbow tables beyond fourteen places in length are not yet common. So, choosing a password that is longer than fourteen characters or that contains non-alphanumeric symbols may force an attacker to resort to brute-force methods.
Certain intensive efforts focused on LM hash, an older hash algorithm used by Microsoft, are publicly available.
[edit] Common uses
Nearly all distributions and variations of Unix, Linux, and BSD use hashes with salts, though many applications use just a hash (typically MD5) with no salt. The Windows NT/2000 family uses the LAN Manager and NT LAN Manager hashing method and is also unsalted, which makes it one of the more popularly generated tables.
[edit] History
Rainbow tables are a refinement of an earlier, simpler algorithm, by Martin Hellman[5] that used the inversion of hashes by looking up precomputed hash chains.
Each table depends on the hash function and the reduce function used. The reduce function is a surjective ("onto") function which maps a hash to a password using the desired character set and password length. Therefore, a reduce function for lowercase alphanumeric passwords of 8 characters length is different from a reduce function for case-sensitive alphanumeric passwords of 5–16 characters length.
A chain is a sequence of passwords. A starting password is chosen, and the following is done to get the next one in the chain:
- reduce(hash(a password)) → next password
After a chain containing a suitable number of passwords is created, the final password in the chain is hashed, and the final hash and the starting password are stored together in the rainbow table.
To reverse a hash, look for it in the table. If it isn't found, the following is done to get another hash to try:
- hash(reduce(a hash)) → next hash
This is repeated until a hash is finally found in the table.
When a match is found, the original password that started the chain that ended with that hash can then be used to generate all the other passwords, and hence hashes, in the chain. Each of the hashes thus generated will be checked against the original target hash, thus hopefully revealing the correct password.
The end result is a table that contains statistically high chance of revealing a password within a short period of time, generally less than a minute. The success probability of the table depends on the parameters used to generate it. These include the character set used, password length, chain length, and table count.
Success probability is defined as the probability that the plaintext can be found for a given ciphertext. In the case of passwords, the password is the plaintext, and the hash of the password is the ciphertext, so the success probability is the probability that the original password can be recovered from the password hash.
[edit] See also
[edit] Notes
- ^ Oechslin, Philippe, Making a Faster Cryptanalytic Time-Memory Trade-Off, http://lasecwww.epfl.ch/~oechslin/publications/crypto03.pdf
- ^ a b Alexander, Steven (June 2004). "Password Protection for Modern Operating Systems". ;login: (USENIX Association) 29 (3). http://www.usenix.org/publications/login/2004-06/pdfs/alexander.pdf.
- ^ Ferguson, Neils; Bruce Schneier (2003). Practical Cryptography. Indianapolis: John Wiley & Sons. ISBN 0-471-22357-3.
- ^ Provos, Niels; David Mazières (1999-06-06). "A Future-Adaptable Password Scheme". Proceedings of the FREENIX Track: 1999 USENIX Annual Technical Conference (Monterey, CA, USA: USENIX Association). http://www.usenix.org/events/usenix99/provos/provos.pdf.
- ^ Hellman Martin, A Cryptanalytic Time - Memory Trade-Off
[edit] References
- Oechslin, Philippe (2003-08-17), "Making a Faster Cryptanalytical Time-Memory Trade-Off", Advances in Cryptology: Proceedings of CRYPTO 2003, 23rd Annual International Cryptology Conference, Lecture Notes in Computer Science (Santa Barbara, CA, USA: Springer), ISBN 3-540-40674-3, http://lasecwww.epfl.ch/~oechslin/publications/crypto03.pdf
[edit] External links
- Project RainbowCrack A rainbow table generator
- Ophcrack page by Philippe Oechslin The original rainbow table research with online demo
- How Rainbow Tables work
- Rainbow Tables FAQ (Section 4) In-depth explanation about Rainbow Tables and how they work
|
|||||||||||||||||||||||||||||||||||